|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2002 |
|
УДК 621.391
ПОМЕХОУСТОЙЧИВЫЕ ГРУППОВЫЕ КОДЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Л.Ф. Бородин
Поступила в редакцию 26.08.02 г.
Разработаны фундаментальные положения теории помехоустойчивых кодов, синтезируемых на основе операций мультипликативной подгруппы поля действительных чисел или модульного ранжирования. Мультипликативныйй групповой двоичный код (МГД-код) записывается в виде переопределенной системы нелинейных уравнений, получаемую, в частности, путем преобразования системы линейных форм группового бинарного кода с помощью стандартных мультипликативных операций или модульного ранжирования. «Покоординатное» умножения векторов и законы композиции конечных последовательностей над полем действительных чисел позволяют с единых позиций обсуждать структурные и метрические особенности пространства МГД-кодов, процессы искажения кодовых комбинаций аддитивными и мультипликативными помехами, решающие процедуры и т.д. Представлены аналоговые модели разнотипных каналов связи, которые при наличии на приемном конце первой решающей схемы реализуются в виде известных дискретных схем трактов передачи типа двоичного симметричного канала, канала со стиранием и др.
ВВЕДЕНИЕ
В статье рассматриваются вопросы, связанные с решением задач потенциальной помехоустойчивостью систем пеpедачи инфоpмации с позиций работ [1 - 4]. Отмечено, что проблема оптимизации системы как единого объекта, предполагает оптимизацию пpоцедуp кодиpования сообщений и синтеза сигналов с избыточностью совместно с процессами обработки «в целом» сложных сигналов и диагностикой паpаметpов канала связи. Для систем с кодовым детектированием (коддетекторных систем) [2 - 4] такая «сквозная» оптимизация систем реализуется с единых концептуальных позиций над полем действительных чисел, включая помехоустойчивое пpедставление семантической инфоpмации, процедур принятие pешения о пеpеданном сообщении, оценок текущего и прогнозного состояния тракта передачи информации.
Данная работа посвящена основам теории мультипликативных групповых двоичных кодов. Множество кодовых комбинаций (векторов) таких МГД-кодов строится с помощью операций мультипликативной подгруппы поля действительных чисел или, адекватной им (в определенном смысле), операций модульного ранжирования [3].
Кодовым пространством МГД-кода названо множество ![]() векторов,
которое может быть образовано путем умножения комбинации (вектора)
векторов,
которое может быть образовано путем умножения комбинации (вектора) ![]() МГД-кода
на
МГД-кода
на ![]() вектор
вектор
![]() (возможно рандомизированный) и сложение полученного таким образом
вектора, вообще говоря, с аналоговым случайным
(возможно рандомизированный) и сложение полученного таким образом
вектора, вообще говоря, с аналоговым случайным ![]() вектором
вектором
![]() . Вектора
. Вектора
![]() и
и ![]() здесь
играют роль «мультипликативной» и «аддитивной» помехи соответственно.
здесь
играют роль «мультипликативной» и «аддитивной» помехи соответственно.
Процедуры умножения и сложения векторов, т.е. процессы искажения кодовых комбинаций «мультипликативной» и «аддитивной» помехами, реализуются с помощью процедуры «покоординатного» умножения векторов и закона композиции конечных последовательностей над полем действительных чисел.
В [3] подчеркнуто - формальное представление МГД-кодов отличается от записи аддитивных групповых бинарных кодов (АГБ-кодов) лишь видом алгебраической операции. Это обстоятельство позволяет широко использовать методологию и фактические материалы монографии [1] для синтеза МГД-кодов, для решения других теоретических и прикладных проблем коддетекторных систем, включая способы построения различных видов помехоустойчивых кодов, дискретные и налоговые методы их декодирования над полем действительных чисел.
1. МЕТОДЫ СИНТЕЗА МГД-КОДОВ
Помехоустойчивое кодирование и переопределенные системы уравнений. Проблемы помехоустойчивого кодирования над
полем действительных чисел здесь, как и в [1 - 4], увязаны с целенаправленным и рациональным синтезом над полем
действительных чисел переопределенной системы ![]() уравнений вида
уравнений вида
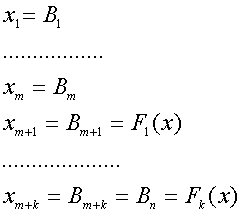 ,
(1)
,
(1)
Для кодов над полем действительных чисел в (1) независимые переменные (информационные символы)
![]() равны либо
равны либо
![]() либо
либо ![]() ;
;
![]() - функция, формирующая
- функция, формирующая
![]() -тый избыточный (контрольный) символ
-тый избыточный (контрольный) символ
![]() кодовой комбинации (вектора)
кодовой комбинации (вектора)
![]() ,
(2)
,
(2)
Синтез МГД-кодов на основе операций мультипликативной коммутативной подгруппы поля действительных чисел.
Множество всевозможных комбинаций (2) приобретает свойства МГД-кода, если в (1) независимые переменные
![]() рассматриваются как элементы мультипликативной подгруппы поля
действительных чисел
рассматриваются как элементы мультипликативной подгруппы поля
действительных чисел ![]() , а
, а
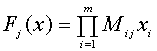 (3)
(3)
Здесь умножение - операция поля действительных чисел и
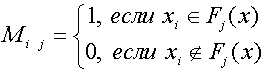 (4)
(4)
Напомним, что фундаментальным свойством элементов мультипликативной подгруппы поля действительных чисел является равенство
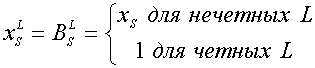 (5)
(5)
Особо подчеркнем - при сделанных предположениях система мультипликативных уравнений (1) является совместной и
определенной (по принципу формирования) Она содержит конечное число подсистем, решение любой из которых совпадает с единственным решением
всей переопределенной системы. Код (1) содержит ![]() всевозможных
всевозможных
![]() значных комбинаций вида (2)
значных комбинаций вида (2)
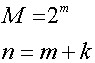 (6)
(6)
МГД-коды и операция модульного ранжирования. В [3] было отмечено, что операция модульного ранжирования записывается так
![]() (7)
(7)
Иначе говоря, полуразность модуля суммы и модуля разности значений
![]() и
и ![]() ,
, имеет знак, который совпадает со знаком их произведения, а абсолютное значение функции (7) равно наименьшему
из модулей исходных величин.
,
, имеет знак, который совпадает со знаком их произведения, а абсолютное значение функции (7) равно наименьшему
из модулей исходных величин.
Если ![]() и
и
![]() могут принимать лишь значения
могут принимать лишь значения
![]() , то из (2) следует
, то из (2) следует
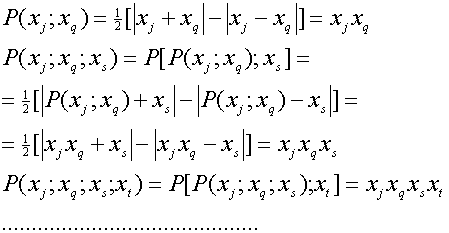 (8)
(8)
Таким образом, для синтеза проверочных символов комбинаций МГД-кодов вместо (3) - (5) можно использовать операции вида (8) [2]. Отметим одну особенность модульного ранжирования
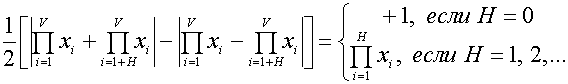 (9)
(9)
При ![]() имеем
имеем
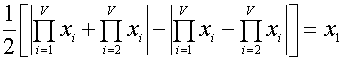 (10)
(10)
Трансформация линейных кодов в МГД-коды . В [3] было подчеркнуто, что формальная запись МГД-кодов
отличается от линейных кодов видом алгебраической операции. Действительно, cистема (1) образует АГБ-код, если независимые переменные
![]() являются элементами
являются элементами
![]() (
(![]() или
или ![]() ), а
), а
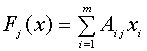 ,
(11)
,
(11)
где суммирование и умножение проводятся по правилам ![]() ,
,
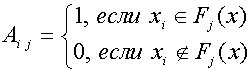 (12)
(12)
Фундаментальным свойством элементов ![]() аддитивной
подгруппы
аддитивной
подгруппы ![]() является равенство
является равенство
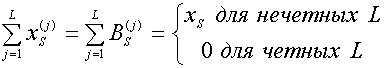 (13)
(13)
Здесь ![]() , а сложение проводится по правилу
, а сложение проводится по правилу![]() т. е. используется операция
т. е. используется операция ![]() . Сопоставление (3) - (5) и (11) - (13)
показывает, что МГД-коды можно строить путем подстановки в формальную запись АГБ-кода вместо независимых переменных
. Сопоставление (3) - (5) и (11) - (13)
показывает, что МГД-коды можно строить путем подстановки в формальную запись АГБ-кода вместо независимых переменных
![]() и
и ![]() значений
значений
![]() соответственно и замены
соответственно и замены
![]() операцией умножения над полем действительных чисел или операцией
модульного ранжирования. Проиллюстрируем сказанное применительно к эквидистантному семизначному
операцией умножения над полем действительных чисел или операцией
модульного ранжирования. Проиллюстрируем сказанное применительно к эквидистантному семизначному
![]() коду с числом информационных символов
коду с числом информационных символов
![]() [1,2]. Комбинация такого кода с учетом (2) и (6) запишется так
[1,2]. Комбинация такого кода с учетом (2) и (6) запишется так
![]() (14)
(14)
Переопределенная система уравнений (1) для эквидистантного семизначного![]() примет вид системы линейных уравнений [1 - 4]:
примет вид системы линейных уравнений [1 - 4]:
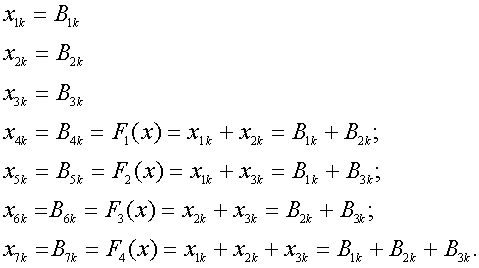 (15)
(15)
В (14) и (15) ![]()
![]() -
независимые переменные, принимающие значения
-
независимые переменные, принимающие значения ![]() или
или
![]() ;
; ![]()
![]() -
избыточные символы, формируемые функциями
-
избыточные символы, формируемые функциями ![]() (11) - (13), т.е. путем
(11) - (13), т.е. путем
![]() соответствующих информационных символов.
соответствующих информационных символов.
Для преобразования системы линейных соотношений (15) в мультипликативную систему уравнений МГД-кода, согласно сказанному выше, надо,
во-первых, полагать, что независимые переменные принимают значения ![]() или
или
![]()
![]() и,
во-вторых, заменить
и,
во-вторых, заменить ![]() операцией умножения над полем
действительных чисел. Таким образом переопределенная система уравнений (1) с учетом (11) –(13) для эквидистантного семизначного
операцией умножения над полем
действительных чисел. Таким образом переопределенная система уравнений (1) с учетом (11) –(13) для эквидистантного семизначного
![]() примет вид системы линейных уравнений [1 - 4] :
примет вид системы линейных уравнений [1 - 4] :
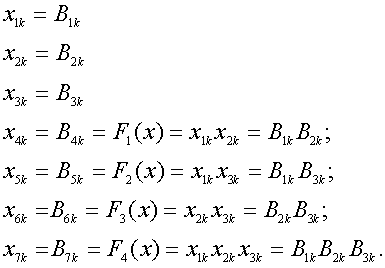 , (16)
, (16)
где, теперь,
![]()
![]() -
независимые переменные
-
независимые переменные ![]() или
или
![]() ;
; ![]()
![]() -
избыточные символы, определяемые функциями
-
избыточные символы, определяемые функциями ![]() (3) – (5), т.е. путем
перемножения значений соответствующих информационных символов.
(3) – (5), т.е. путем
перемножения значений соответствующих информационных символов.
Используя в (16) вместо умножения операцию модульного ранжирования (8) получим запись системы уравнений (15) в виде переопределенной системы модульно-ранговых уравнений:
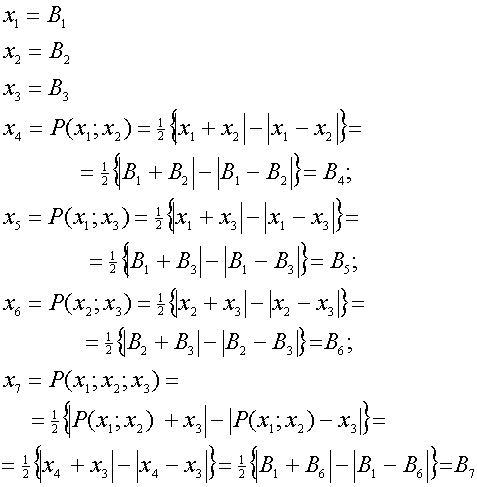 (17)
(17)
Методом трансформации линейных кодов можно образовать МГД-коды:
- циклические, включая ![]() ;
;
- рекурентные Финка - Хагельбаргера;
- итеративные;
- с заданным кодовым расстоянием;
- с синдромным, иными алгоритмами обнаружения и исправления ошибок;
- эквидистантные и другие оптимальные (в смысле [2]) и т. д.
1. КОДОВОЕ ПРОСТРАНСТВО, УМНОЖЕНИЕ И СЛОЖЕНИЕ
КОМБИНАЦИЙ МГД-КОД
Кодовым пространством МГД-кода названо множество
![]() векторов, которое может быть образовано путем умножения комбинации
(вектора)
векторов, которое может быть образовано путем умножения комбинации
(вектора) ![]() МГД-кода на
МГД-кода на
![]() вектор
вектор ![]() (возможно
рандомизированный) и сложение полученного таким образом вектора, вообще говоря, с аналоговым случайным
(возможно
рандомизированный) и сложение полученного таким образом вектора, вообще говоря, с аналоговым случайным
![]() вектором
вектором
![]() . Вектора
. Вектора
![]() и
и ![]() играют
роль «мультипликативной» и «аддитивной» помехи соответственно.
играют
роль «мультипликативной» и «аддитивной» помехи соответственно.
Процедуры умножения и сложения векторов, т.е. процессы искажения кодовых комбинаций «мультипликативной» и «аддитивной» помехами, реализуются с помощью процедуры «покоординатного» умножения векторов и закона композиции конечных последовательностей над полем действительных чисел.
МГД-код как коммутативная мультипликативная группа. Правило умножения комбинации
![]() МГД-кода на вектор
МГД-кода на вектор
![]() определим как «покоординатное» умножение двух
определим как «покоординатное» умножение двух
![]() -мерных векторов
-мерных векторов
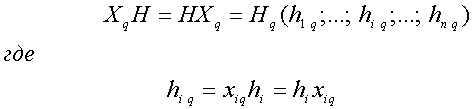 ,
(18)
,
(18)
В частном случае, когда вектор ![]() (координаты
вектора
(координаты
вектора ![]() совпадают с символами комбинации
совпадают с символами комбинации
![]() ) из (18) получим
) из (18) получим
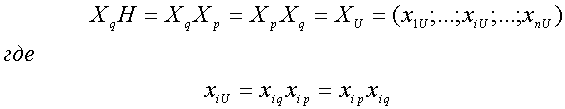 , (19)
, (19)
Операция (19), совместно с (3) - (5), превращают комбинации ![]() кодов
(1) и (16) в элементы коммутативной мультипликативной группы. При этом комбинации
кодов
(1) и (16) в элементы коммутативной мультипликативной группы. При этом комбинации
![]() ,
, ![]()
![]() (19)
принадлежат одному и тому же МГД-коду (свойство замкнутости группы).
(19)
принадлежат одному и тому же МГД-коду (свойство замкнутости группы).
При умножение комбинации ![]() МГД-кода самой на себя
имеем
МГД-кода самой на себя
имеем
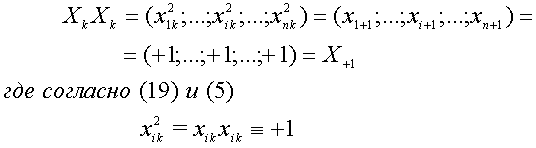 (20)
(20)
Комбинация
![]() (20) является нейтральным элементом группы
(20) является нейтральным элементом группы
![]() (21)
(21)
Для дискретного или аналогового (в том числе и случайного)
![]() поля действительных чисел имеют место равенства
поля действительных чисел имеют место равенства
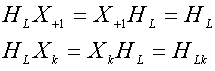 (22)
(22)
Операции с комбинациями МГД-кода в векторном пространство конечных последовательностей действительных чисел.
Сложение кодовой комбинации ![]() с вектором
с вектором
![]() и умножение
и умножение
![]() на действительное число
на действительное число
![]() будем выполнять по законам композиции конечных последовательностей
действительных чисел:
будем выполнять по законам композиции конечных последовательностей
действительных чисел:
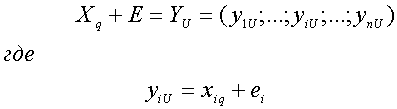 ,
(23)
,
(23)
одновременно,
![]() (24)
(24)
При сложении кодовых комбинаций ![]() и
и
![]() имеем
имеем
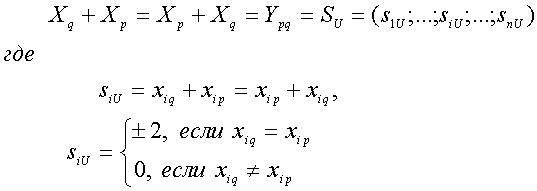 (25)
(25)
3. МЕТРИКА И РАССТОЯНИЕ В ПРОСТРАНСТВЕ МГД-КОДОВ
Множество кодовых комбинаций приобретет свойства метрическое пространство, если для комбинаций
![]() и
и ![]() определена
однозначная неотрицательная функция
определена
однозначная неотрицательная функция
![]() ,
(26)
,
(26)
удовлетворяющую трем аксиомам:
1.![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
2.
![]() (аксиома симметрии).
(аксиома симметрии).
3.
![]() (аксиома треугольника).
(аксиома треугольника).
В теории кодирования величину
![]() называют кодовым расстоянием между комбинациями
называют кодовым расстоянием между комбинациями
![]() и
и ![]() и
задают так
и
задают так
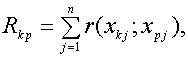 (27)
(27)
где функция
![]() определяет меру (метрику) кода (1).
определяет меру (метрику) кода (1).
Для меры Хэмминга
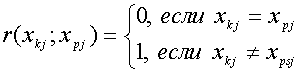 (28)
(28)
Следовательно, расстояние (27) между кодовыми комбинациями ![]() и
и
![]() равно
равно
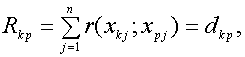 (29)
(29)
где ![]() - суммарное число позиций, на
которых символы комбинации
- суммарное число позиций, на
которых символы комбинации ![]() и
и
![]() отличаются друг от друга.
отличаются друг от друга.
При квадратичной метрике
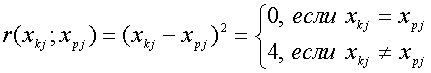 (30)
(30)
и расстояние (27) равно
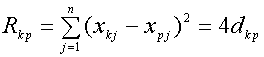 (31)
(31)
При модульной (абсолютной) мере
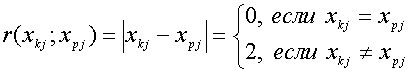 (32)
(32)
и расстояние (27) равно
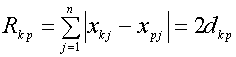 (33)
(33)
В (31) и (33) ![]() имеет
прежний смысл (29).
имеет
прежний смысл (29).
Из проведенных выкладок следует, что расстояния в кодовом пространстве при квадратичной и модульной метриках кратны кодовому расстоянию для меры Хэмминга.
Спектр кодовых расстояний МГД-кода. Набор величин
![]() образует спектр кодовых расстояний
образует спектр кодовых расстояний
![]() (34)
(34)
Матрица (34) имеет ![]() (6) строк и
(6) строк и
![]() столбцов (6). Для МГД-кода, как группового кода, численные значения
элементов (34) наиболее просто определяются в виде расстояния
столбцов (6). Для МГД-кода, как группового кода, численные значения
элементов (34) наиболее просто определяются в виде расстояния ![]() каждой
комбинации
каждой
комбинации ![]() от комбинации
от комбинации
![]() . Величину
. Величину
![]() называют весом комбинации
называют весом комбинации
![]() . Значение
. Значение
![]() совпадает с числом символов
совпадает с числом символов
![]() в комбинации
в комбинации
![]() . Благодаря такому подходу матрица (34) трансформируется в вектор
. Благодаря такому подходу матрица (34) трансформируется в вектор
![]() (35)
(35)
Среди значений ![]() особый интерес представляет величина
особый интерес представляет величина
![]() (36)
(36)
Оптимальными в смысле Хэмминга называют коды, в которых величина
![]() максимальна при фиксированных значениях
максимальна при фиксированных значениях
![]() и
и ![]() (значность
кода и число информационных символов соответственно). Одновременно, МГД-коды оптимальные в смысле Хэмминга оказываются оптимальными в
смысле максимума минимального кодового расстояния при модульной и квадратичной метриках. Напомним, что расстояния в кодовом
пространстве при квадратичной и модульной метриках кратны кодовому расстоянию для меры Хэмминга.
(значность
кода и число информационных символов соответственно). Одновременно, МГД-коды оптимальные в смысле Хэмминга оказываются оптимальными в
смысле максимума минимального кодового расстояния при модульной и квадратичной метриках. Напомним, что расстояния в кодовом
пространстве при квадратичной и модульной метриках кратны кодовому расстоянию для меры Хэмминга.
4. МОДЕЛИ КАНАЛОВ СВЯЗИ
Искаженная кодовая комбинация и разнотипные тракты передачи информации. Воздействие помехи на переданную в
S-тый момент времени комбинацию ![]() выражается
в появление на входе решающего устройства случайного вектора
выражается
в появление на входе решающего устройства случайного вектора
![]() ,
(37)
,
(37)
где ![]() и
и
![]() - текущие реализации рандомизированных векторов
- текущие реализации рандомизированных векторов
![]() и
и ![]() ,
играющих роль «мультипликативной» и «аддитивной» помехи соответственно
,
играющих роль «мультипликативной» и «аддитивной» помехи соответственно
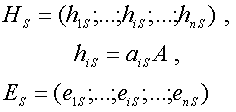 (38)
(38)
Здесь ![]() ,
,
![]() -
-
![]() -тые координаты векторов
-тые координаты векторов
![]() и
и
![]() соответственно;
соответственно;
![]() - случайный коэффициент (
- случайный коэффициент (![]() );
);
![]() - положительная константа, имеющая смысл
«амплитуды»
- положительная константа, имеющая смысл
«амплитуды» ![]() .
.
Введенные определения позволяют записать (37) в виде
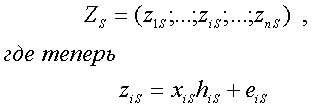 (39)
(39)
В (39), напомним,
![]() -
-
![]() -тый символ кодовой комбинации
-тый символ кодовой комбинации
![]() .
.
Выражения (37) - (39) позволяют описывать модели разнотипных трактов
передачи. К ним относятся модели каналов с аддитивной помехой ![]() и с
замираниями (
и с
замираниями (![]() ). Ситуация
). Ситуация
![]() типична для модели тракта передачи с полным локальным «поглощением»
типична для модели тракта передачи с полным локальным «поглощением»
![]() символа ( канал со стиранием). Случай
символа ( канал со стиранием). Случай
![]() характерен для тракта передачи, где возможен перескок фазы символа на
характерен для тракта передачи, где возможен перескок фазы символа на
![]() и снижение уровня полезного сигнала и т. д.
и снижение уровня полезного сигнала и т. д.
Пусть
![]() (40)
(40)
плотности распределения вероятности компоненты
![]() вектора
вектора
![]() (39) при условии
(39) при условии
![]() соответственно. Тогда, при наличии на приемном конце первой решающей
схемы, представленные выше модели трактов передачи весьма просто реализуются в виде известных дискретных схем двоичного симметричного
канала, канала со стиранием и др.
соответственно. Тогда, при наличии на приемном конце первой решающей
схемы, представленные выше модели трактов передачи весьма просто реализуются в виде известных дискретных схем двоичного симметричного
канала, канала со стиранием и др.
При заданных распределениях (40) этот круг задач решается, как известно, путем выбора уровней разграничения областей принятия
той или иной гипотезы. При этом в дискретном двоичном симметричном канале величина
![]() «демодулируется» правильно (как символ
«демодулируется» правильно (как символ
![]() ) с вероятностью
) с вероятностью
![]() и ошибочно (как символ
и ошибочно (как символ
![]() ) с вероятностью
) с вероятностью
![]() . В дискретном двоичном симметричном канале со стиранием величина
. В дискретном двоичном симметричном канале со стиранием величина
![]() с вероятностью
с вероятностью
![]() оказывается в области правильного приема, попадает в зону
неопределенности с вероятностью
оказывается в области правильного приема, попадает в зону
неопределенности с вероятностью ![]() , интерпретируется ошибочно (как
символ
, интерпретируется ошибочно (как
символ ![]() ) с вероятностью
) с вероятностью
![]() .
.
ЗАКЛЮЧЕНИЕ
Рассмотренные в статье фундаментальные положения теории
корректирующих кодов базируются на использование символов ![]() как
элементов мультипликативной подгруппы поля действительных чисел [2 - 4]. Формальная запись таких помехоустойчивых мультипликативных
групповых двоичных кодов (МГД-кодов) имеет вид переопределенной нелинейной системой уравнений. Например, мультипликативной системой вида
(16) или набором модульно-ранговых уравнений типа (17). Подчеркнем, операция модульного ранжирования адекватна (в определенном смысле)
традиционному умножению.
как
элементов мультипликативной подгруппы поля действительных чисел [2 - 4]. Формальная запись таких помехоустойчивых мультипликативных
групповых двоичных кодов (МГД-кодов) имеет вид переопределенной нелинейной системой уравнений. Например, мультипликативной системой вида
(16) или набором модульно-ранговых уравнений типа (17). Подчеркнем, операция модульного ранжирования адекватна (в определенном смысле)
традиционному умножению.
МГД-коды могут синтезироваться путем трансформации системы линейных форм групповых бинарных кодов в нелинейную систему уравнений с помощью операций мультипликативной подгруппы поля действительных чисел или модульного ранжирования. Это обстоятельство открывает возможности широкого использования теоретических и прикладных положений современной теории бинарных линейных кодов для создания разноплановых оптимальных, циклических, итеративных, рекуррентных и других специальных кодов над полем действительных чисел.
Операции «по координатного» умножения векторов и законы композиции векторного пространства конечных последовательностей над полем действительных чисел обеспечивают единство концептуального описания пространства МГД-кодов и вычисления кодовых расстояний при различных метриках, а также процессов искажения кодовых комбинаций помехами и создание моделей разнохарактерных каналов связи.
Использованный единый математический аппарат и конкретные оригинальные результаты данного исследования открывают большие возможности для решения фундаментальных проблем потенциальной помехоустойчивости коддетекторных систем пеpедачи инфоpмации. Тот факт, что расстояния в пространстве МГД-кодов при квадратичной и модульной метриках кратны кодовому расстоянию для меры Хэмминга, облегчает поиск оптимальной и субоптимальной обработки кодовых комбинаций и сложных сигналов, искаженных аддитивными и мультипликативными помехами, упрощает создание эффективных процедур диагностики значимых параметров тракта передачи сообщений по сигналам несущим основную информацию.
Данная работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований - грант 01 - 01 - 00037.
СПИСОК ЛИТЕРАТУРЫ
1. Бородин Л.Ф. Введение в теорию помехоустойчивого кодирования. Монография, 21.5 усл.п.л., Москва, Советское радио, 1968 г.
2. Бородин Л.Ф., Куцевич И.В.,Черников А.А. Мультипликативное кодирование и кодовое детектирование составных кодированных фазоманипулированных сигналов. Радиотехника и Электроника, т.41, №4, 1996 г. с.450-455.
3. Бородин Л.Ф. Вопросы потенциальной помехоустойчивости составных кодированных фазоманипулированных сигналов. Радиотехника и электроника, т. 43, №10, 1998 г., с.1221-1237.
4. Бородин Л.Ф., Крапивин В.Ф., Березин Ю.В., Левшин И.П., Черников А.А. Идеальный и субидельный приемники составных кодированных фазоманипулировнных сигналов. Зарубежная радиоэлектроника. Успехи современной радиоэлектроники, №7, 1998 г., с.15-21.