| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 1999 |
А.С. Ильин*, В.В. Кулагин**, В.А. Черепенин
**Институт
Радиотехники и Электроники Российской Академии
Наук,
**Государственный Астрономический институт им. П.
К. Штернберга Московского государственного
университета им. М. В. Ломоносова.
Получена 19 января 1999 г.
Введение
Микроскопические модели классических сред известны давно
[1], однако интерес к ним (особенно в последнее время) не ослабевает. Научные акценты в этой проблематике смещены сейчас в сторону численных методов анализа взаимодействия классического электромагнитного поля и заряженных частиц. Задачи подобного типа рассматриваются, например, в физике плазмы, теории ускорителей, микроволновой электронике [2-5]. Различные способы совместного решения уравнений Максвелла и уравнений движения электронов или ионов составляют основное содержание современных моделей классических сред. В зависимости от типа задачи и мощности используемых вычислительных ресурсов трехмерная задача решения уравнений движения может быть редуцирована в шестимерном фазовом пространстве, причем её размерность уменьшается либо в пространстве скоростей, либо в пространстве координат. Таковы, например, довольно часто используемые в релятивистской высокочастотной электронике плоские и аксиально-симметричные 2- и 2.5-мерные модели электронных пучков [6-8]. Как правило, в таких схемах решение самосогласованной задачи может быть существенно упрощено и сведено в основном к решению уравнений движения.В данной работе рассматривается (3+1)-модель заряженной среды, частицы которой имеют три скорости и одну координату. Эта модель существенно отличается от известной безызлучательной модели заряженных листов, где имеется лишь одна соответствующая координате компонента скорости
[5], и может быть применена к более широкому классу задач, в которых излучение играет существенную роль. В частности, получено выражение для поля излучения тонкой заряженной плоскости, совершающей поступательное движени. Найдена сила радиационного трения (самодействия) плоскости и выписаны точные релятивистские уравнения движения с учетом этой силы. Рассмотрена задача о взаимодействии плоскости с электромагнитной волной и найдена сила давления волны на плоскость. Решена задача о генерации третьей гармоники за счет продольных смещений при взаимодействии плоскости с электромагнитной волной. Изучена динамика большого числа плоскостей, взаимодействующих друг с другом и внешней электромагнитной волной.Предложенная модель использована также для исследования статистики электромагнитного поля, взаимодействующего со слоем электронов. Показано, что при определенных условиях состояния поля могут быть неклассическими. Неклассический свет представляет собой излучение, в котором флуктуации некоторых параметров ниже так называемого стандартного квантового уровня, соответствующего когерентному излучению
.Неклассические состояния электромагнитного поля экспериментально обнаружены уже более тринадцати лет назад [9,10], и в настоящее время интенсивно исследуются возможности применения этих состояний электромагнитного поля, в частности, в области экспериментов с пробными телами
, квантовых измерений, систем связи, квантовой криптографии и др. К сожалению, полученные экспериментально коэффициенты сжатия (неклассичности) оказываются весьма скромными. Это связано с тем, что основу большинства методов получения неклассического света составляют нелинейные оптические процессы. Подавление квантовых флуктуаций оказывается, как правило, тем выше, чем выше эффективность нелинейного процесса. Однако, конкурирующие диссипативные эффекты существенно снижают результирующий коэффициент сжатия.Системы со свободными электронами являются перспективными в плане получения значительных коэффициентов сжатия, так как нелинейность может быть существенной при малой диссипации. Простейшая схема генерации сжатых состояний в электронной среде рассмотрена в работе [11]. При этом использована феноменологическая модель электронных зеркал, в которой коэффициент преломления электромагнитной волны внутри зеркала определялся концентрацией электронов. Однако, такая модель не позволила учесть ряд эффектов, в частности, группировку электронного пучка, взаимодействие электронных зеркал с полем стоячей волны, динамику деформации слоя электронов и др.
В разделах 7 и 8 с помощью предлагаемой модели исследуется генерация сжатых состояний электромагнитного поля для режима бегущих и стоячих волн.1. Одномерное распределение зарядов и токов. Функция Грина и выражения для напряженностей электромагнитного поля.
Пусть плотности заряда
В калибровке Лоренца уравнения для потенциалов имеют следующий вид
[12]: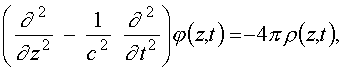 (1)
(1)
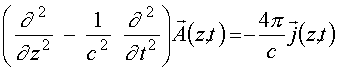 .
.
Решение уравнений (1) можно представить в виде
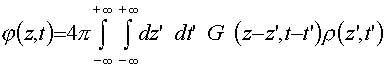 , (2)
, (2)
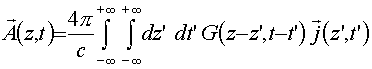 ,
,
где
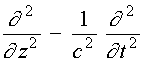 , удовлетворяющая уравнению
, удовлетворяющая уравнению
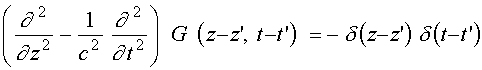 . (3)
. (3)
Кроме того, функция Грина должна удовлетворять условию причинности
:![]()
которое означает, что возмущение возникает только после начала действия источника.
Решения уравнения (3) с граничным условием (4) можно найти следующим образом
[13]. В уравнении (3) разложим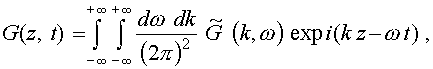 (5)
(5)
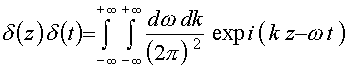 . (6)
. (6)
Подставляя (5) и (6) в (3), найдем уравнение для фурье-образа
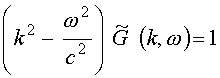
или
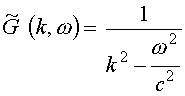 . (7)
. (7)
Для функции
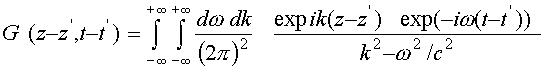 . (8)
. (8)
Однако выражение (8) дает только формальное решение уравнения (3), так как не определено правило интегрирования особенностей (8) при
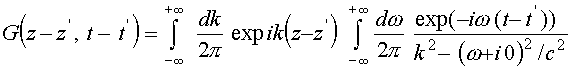 .(9)
.(9)
Пользуясь известной леммой Жордана из теории функций комплексной переменной, можно показать, что при таком способе интегрирования (8) условие причинности (4) выполнено. При
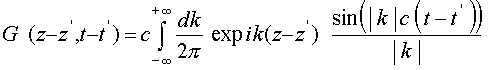 .
.
Выполняя далее интегрирование по
k, можно получить окончательное выражение для функции Грина: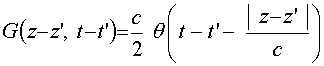 . (10)
. (10)
Здесь
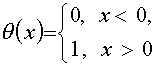
- ступенчатая функция Хевисайда.
Как можно заметить, для реальных источников электромагнитного поля
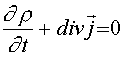 для таких зарядов и токов не
выполняется. Однако если теперь перейти от
потенциалов к напряженностям электромагнитного
поля по формулам
для таких зарядов и токов не
выполняется. Однако если теперь перейти от
потенциалов к напряженностям электромагнитного
поля по формулам
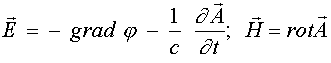 (11)
(11)
и устремить параметр
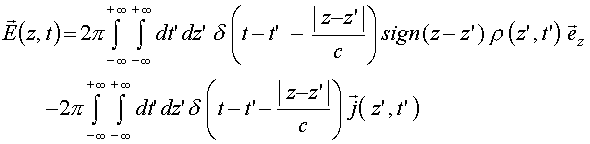 (12)
(12)
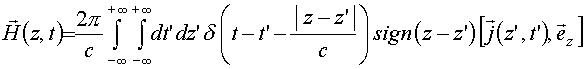 .
.
Здесь
Или после интегрирования по
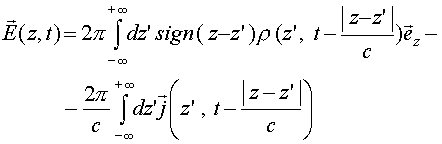
(13)
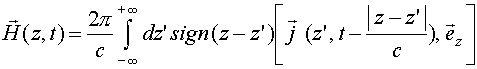 .
.
2. Поле излучения тонкой заряженной плоскости
Получим выражение для электромагнитного поля, создаваемого тонкой заряженной плоскостью. Будем полагать, что движение плоскости поступательное. В этом случае для его описания нам понадобятся 3+1 функции времени: три компоненты скорости
Для бесконечно тонкой плоскости плотности заряда и тока имеют следующий вид:
![]() , (14)
, (14)
где
Подставляя теперь выражения (14) в уравнения (12) и интегрируя по
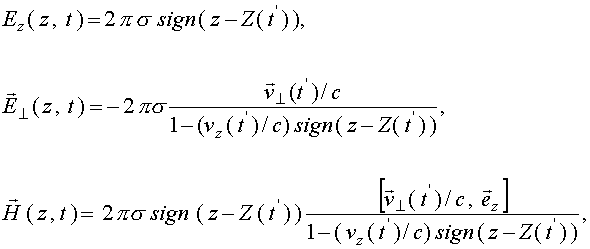 (15)
(15)
где
Заметим, что выражения (15) являются одномерными (или, точнее, 3+1- мерными) аналогами потенциалов Лиенара – Вихерта
[9] и дают точное решение задачи о поле, создаваемом бесконечной плоскостью, при этом компонентаВ случае, когда плоскость движется перпендикулярно оси
0z (координата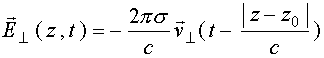
Анализ выражения (15а) показывает, что поле излучения плоскости пропорционально ее скорости
Сделаем теперь замечание относительно поведения решений (15) при преобразованиях Лоренца. Напомним, что при выводе уравнений (15) предполагали, что плоскость движется как целое, т.е. в каждый момент времени все точки плоскости имеют одинаковые скорости. Однако в силу относительности одновременности это свойство движения будет нарушено при переходе в другую систему отсчета (если только скорость
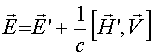 , справедливых при
, справедливых при ![]()
или, когда компонента
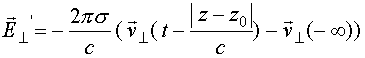 .
.
Так как поперечное электрическое поле (15б) отличается от входящего в (15) поперечного поля на слагаемое, не зависящее ни от времени, ни от координаты, то оно также удовлетворяет уравнениям Максвелла и, кроме того, обладает ковариантностью относительно преобразований Галилея.
Далее для простоты будем пользоваться уравнениями (15) вместо (15б), полагая, что плоскость в далеком прошлом покоилась.
3. Сила радиационного трения
В случае точечного заряда задача о нахождении уравнений движения с учетом собственного поля излучения сопряжена с многочисленными трудностями (перенормировка массы, самоускорение и т.д.)
[14,15]. Формально эти трудности возникают из-за того, что поле в точке нахождения источника обладает сингулярностью. В отличие от поля точечного заряда решения (15) не содержат сингулярностей, поэтому возможно точно и корректно решить задачу о взаимодействии плоскости с собственным полем излучения. Для этого определим поле в точке
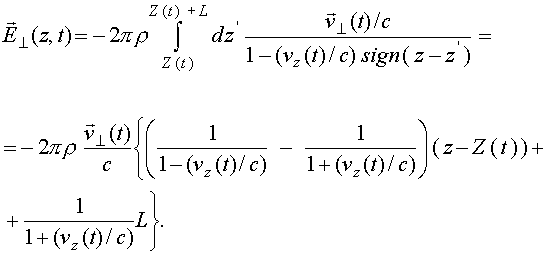
Так как поле внутри слоя зависит от координаты
z линейно, среднее поле будет равно полусумме полей на краях слоя. Устремляя теперь L к нулю, видим, что поля в точке разрыва следует полагать равными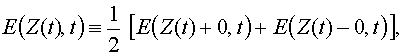
(16)
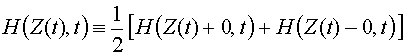 .
.
В результате для полей самодействия плоскости имеем
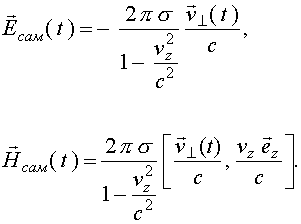 (17)
(17)
Отметим, что z-компоненты полей самодействия равны нулю:
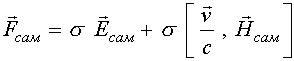 или в
компонентах
или в
компонентах
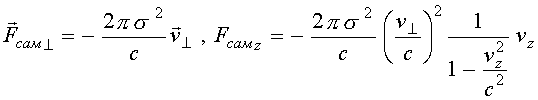 (18)
(18)
Уравнение движения плоскости во внешнем однородном по координатам
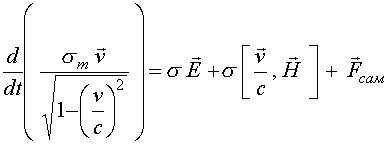 ,
(19)
,
(19)
где
Таким образом, выражение (19) является точным уравнением поступательного движения заряженной плоскости с учетом силы радиационного трения. Учет сил самодействия приводит к появлению эффективной «вязкой»
силы с коэффициентом вязкости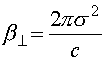 для
поперечного движения. В то же время продольная
сила радиационного трения
для
поперечного движения. В то же время продольная
сила радиационного трения 4. Взаимодействие электронного листа с плоской электромагнитной волной
Пусть для определенности заряженная плоскость образована тонким слоем электронов, бесконечно протяженным в
x и y направлениях. Такую структуру будем называть электронным листом. Если электроны в процессе движения все время образуют плоский лист с постоянной поверхностной плотностью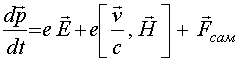 ,
,
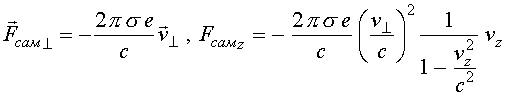
Здесь
Это приближение будет справедливо, если изменением конфигурации плоского электронного листа можно пренебречь, что возможно в течение ограниченного времени при достаточно малой
концентрации электронов либо в присутствии ионного фона, когда силы кулоновского расталкивания скомпенсированы. В то же время концентрация электронов должна быть достаточной для того, чтобы считать заряд непрерывно распределенным по листу.Следует отметить, что эта же модель может быть применена и к листу конечных размеров, если время прибытия сигнала с краев существенно больше характерных периодов процесса
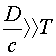 , (21)
, (21)
где
Пусть теперь на электронный лист, расположенный в точке
![]() , (22)
, (22)
где
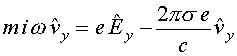 , откуда
получим следующее выражение для комплексной
амплитуды скорости
, откуда
получим следующее выражение для комплексной
амплитуды скорости 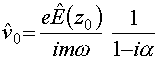 , (23)
, (23)
где
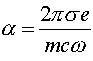 и
для поля, излучаемого листом, из выражения (15а)
имеем
и
для поля, излучаемого листом, из выражения (15а)
имеем
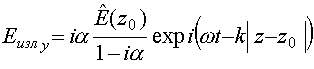 . (24)
. (24)
Нетрудно показать, что при
![]() ,
,
и полное поле равно нулю, в то время как поле слева описывается выражением
и полное поле представляет собой стоячую волну
![]() .
.
Найдем теперь среднюю по периоду поля силу давления, возникающую при взаимодействии электромагнитной волны с плоским электронным листом. Если при взаимодействии точечного заряда с плоской электромагнитной волной не учитывать радиационные потери, то движение заряда будет происходить по замкнутой траектории
[12], т.е. средняя по периоду сила давления волны на электрон равна нулю. Поэтому для вычисления силы давления принципиально необходимо учитывать радиационное трение (самодействие плоскости). Пусть опять на электронный лист перпендикулярно плоскости падает электромагнитная волна. В направлении оси Oz на электрон действует сила Лоренца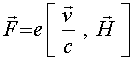 , которая и
определяет величину силы давления. Если в
выражении (23) не учитывать член, связанный с
радиационным трением (полагать
, которая и
определяет величину силы давления. Если в
выражении (23) не учитывать член, связанный с
радиационным трением (полагать Используя полное выражение для скорости электронов (23) с учетом силы радиационного трения, получим следующее выражение для средней по периоду
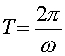 силы Лоренца,
действующей на один электрон:
силы Лоренца,
действующей на один электрон:
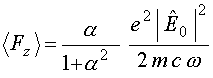 .
(25)
.
(25)
Интересно отметить, что выражение (25) имеет максимум при
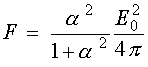 . Таким
образом, сила давления на единицу площади
максимальна при выполнении условия полного
отражения волны от электронного листа (
. Таким
образом, сила давления на единицу площади
максимальна при выполнении условия полного
отражения волны от электронного листа (Рассмотрим теперь отражение плоской электромагнитной волны от электронного листа в присутствии однородного магнитного поля с напряженностью
![]() (26)
(26)
(x
и y-компоненты векторов предполагаем вещественными). Рассматривая для определенности электромагнитную волну с круговой поляризацией, запишем для нее следующие выражения:![]() . (27)
. (27)
Уравнения движения электронов (20) на частоте
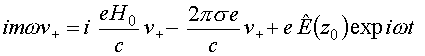 , (28)
, (28)
где
Далее для поперечной скорости имеем
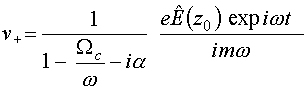 , (29)
, (29)
где
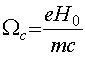 -
циклотронная частота вращения электронов.
-
циклотронная частота вращения электронов.
Для поля излучения листа из (15) и (29) найдем
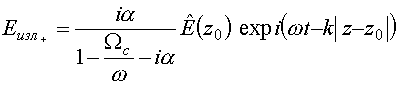 . (30)
. (30)
В результате для прошедшей и отраженной волн получим следующие выражения:
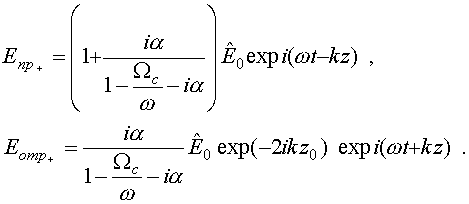 (31)
(31)
Как и следовало ожидать, в точке циклотронного резонанса при
![]() . (32)
. (32)
Отметим, что в этом случае коэффициент отражения волны не зависит от концентрации электронов, так как при циклотронном резонансе амплитуда скорости становится обратно пропорциональной
Подсчитаем теперь силу давления, которое оказывает волна на один электрон тонкого электронного листа в присутствии однородного магнитного поля. Для силы Лоренца, возникающей при взаимодействии электронов с магнитной составляющей волны круговой поляризации, справедливо выражение
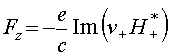 или при
использовании (27)
или при
использовании (27) 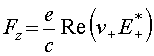 . Здесь в
отличие от рассмотренного ранее случая линейно
поляризованной волны стоит точная сила,
неусредненная по периоду колебаний электронов.
. Здесь в
отличие от рассмотренного ранее случая линейно
поляризованной волны стоит точная сила,
неусредненная по периоду колебаний электронов.
Используя теперь (27) и (29), запишем окончательное выражение для силы давления на плоскость в присутствии продольного магнитного поля:
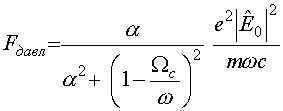 .
(33)
.
(33)
В точке циклотронного резонанса сила (33) растет при уменьшении плотности
6. Учет продольных смещений электронного листа. Генерация третьей гармоники
Рассмотрим теперь точные релятивистские уравнения движения электронного листа в поле электромагнитной волны. Пусть для напряженностей электрического и магнитного полей волны справедливы выражения
а остальные компоненты равны нулю. Уравнения движения электронного листа (20) имеют следующий вид:
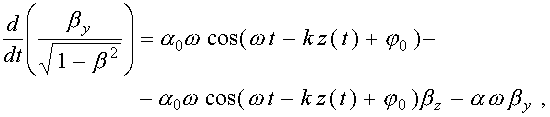 (34)
(34)
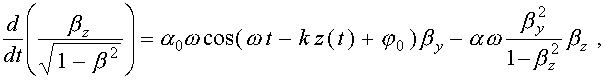
где
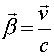 -
релятивистская скорость электронов,
-
релятивистская скорость электронов, 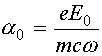 -
ускорительный параметр.
-
ускорительный параметр.
Считая
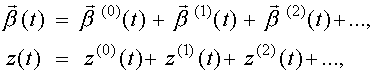 , (35)
, (35)
где члены
Подставляя разложения (35) в (34) и группируя члены одинакового порядка малости по
![]() (36)
(36)
Уравнения для первого приближения
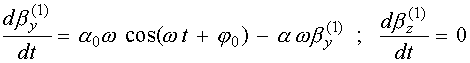 (37)
(37)
на частоте
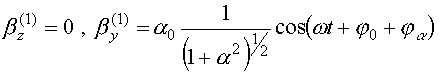 , (38)
, (38)
где
![]() (39)
(39)
- фазовая задержка. Выражения (38),(39) тождественны (23). Таким образом, полученные в разд.4 решения справедливы в линейном приближении по ускорительному параметру
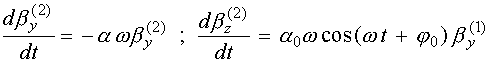 , (40)
, (40)
откуда
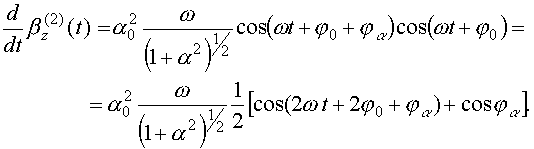
Здесь первое слагаемое описывает быстрые осцилляции на двойной частоте, а второе - медленный дрейф под действием силы давления (25). Будем полагать, что сила давления скомпенсирована действием некоторой внешней силы и рассматривать только быстрые осцилляции. В результате для продольной скорости и координаты получим следующие выражения:
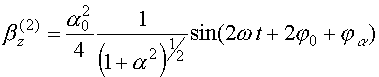 , (41)
, (41)
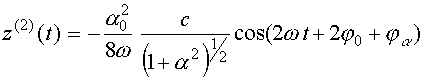 . (42)
. (42)
Далее нам понадобится кубическая поправка к поперечной скорости
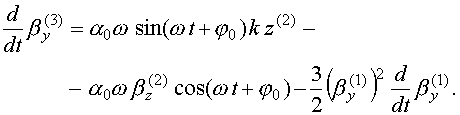
Здесь первые два слагаемых возникают из-за продольного движения листа, а последнее слагаемое описывает релятивистские поправки. Интегрируя это уравнение по времени, получим для
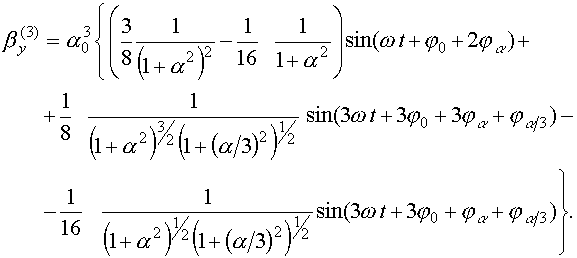 (43)
(43)
Выражение для запаздывающего времени с точностью до
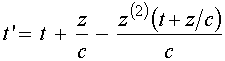 . (44)
. (44)
Поле излучения можно представить теперь в виде суммы линейного по
![]() , (45)
, (45)
где излучение на частоте
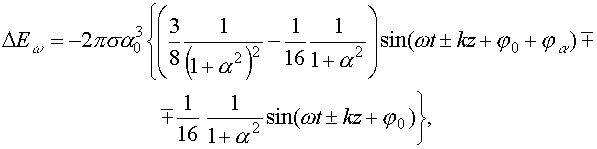
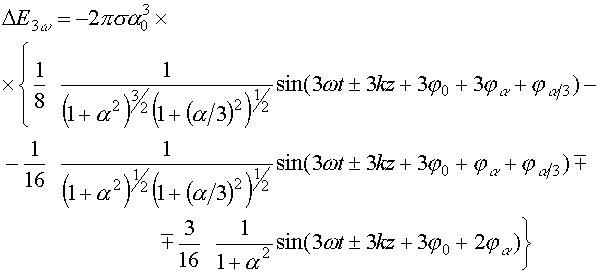
Верхний знак относится к отраженной волне, нижний знак – к прошедшей. Таким образом, продольные колебания листа приводят к генерации третьей гармоники как в прошедшей, так и в отраженной волне. Нетрудно показать, что если пренебречь временной дисперсией электронной среды и релятивистскими поправками, третьей гармоники в прошедшей волне не будет, а в отраженной волне она сохранится.
7. Генерация сжатых состояний электромагнитного поля при падении световой волны на тонкий электронный слой.
Пусть на тонкий электронный слой, находящийся в потенциальной яме
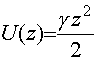 с жесткостью
с жесткостью ![]() ,
(46)
,
(46)
где
При падении такой волны на электронный слой возникает сила давления согласно выражению (25), квадратично зависящая от амплитуды падающей волны. Эта сила давления вызывает смещение слоя в потенциальной яме, т. е. изменяется координата плоскости, и появляется дополнительное запаздывание отраженной волны. В результате возникает квадратичная зависимость фазы отраженной волны от амплитуды падающей.
Пусть для простоты параметр
![]() , (47)
, (47)
где
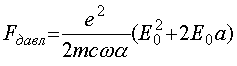 . (48)
. (48)
Положение слоя
![]() , (49)
, (49)
где
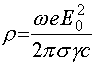 .
Из выражения (49) следует, что квадратурные
компоненты шума в отраженной волне
коррелированы, причем коэффициент корреляции
тем больше, чем больше параметр
.
Из выражения (49) следует, что квадратурные
компоненты шума в отраженной волне
коррелированы, причем коэффициент корреляции
тем больше, чем больше параметр 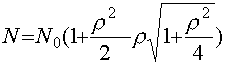 , (50)
, (50)
где
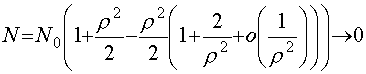
Таким образом, коэффициент сжатия поля может быть сколь угодно большим в рамках использованной модели.
Потенциальная яма для электронов может быть образована, например, двумя заданными встречными волнами одинаковой амплитуды
![]() .
(51)
.
(51)
Для решения уравнений движения электронов в поле такой волны воспользуемся дрейфовым приближением
[18], т.е. представим движение электронов как сумму быстрых осцилляций вдоль оси Oy и медленный дрейф вдоль оси Oz. Дрейфовая составляющая радиуса-вектора электронов определяется усредненной по периоду быстрых колебаний силой Лоренца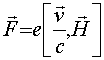 . Используя
тождество:
. Используя
тождество: 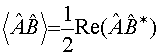 , где
, где 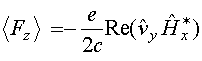 .
.
Используя выражение (23) получаем окончательно:
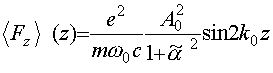 , (52)
, (52)
где
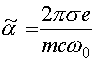 .
.
Положение устойчивого равновесия
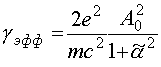 . (53)
. (53)
Следует отметить, что в отсутствии падающей на слой электромагнитной волны электроны, находящиеся в узлах электрического поля стоячей волны, не излучают.
8. Генерация сжатых состояний при взаимодействии с полем стоячей волны.
Посмотрим теперь, нельзя ли получить сжатое состояние электромагнитного поля только за счет взаимодействия тонкого электронного слоя с полем стоячей волны.
Пусть на электронный слой падают две встречные волны с произвольными комплексными амплитудами
![]() .
(54)
.
(54)
Проводя вычисления, аналогичные пункту 6, получим для средней дрейфовой силы вдоль оси
Oz: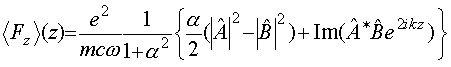 . (55)
. (55)
Первый член в выражении (55) описывает динамическое давление за счет разности амплитуд волн, второй - эффекты группировки ( ср. выражения (25) и (52) ).
Пусть теперь
![]() .
.
Из выражения (55), в линейном приближении по шумам, имеем для силы вдоль оси Oz:
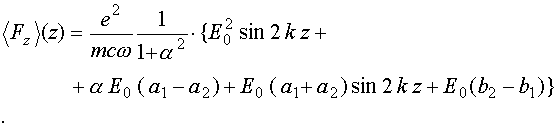 (56)
(56)
В результате, в том же приближении, для положения устойчивого равновесия электронов
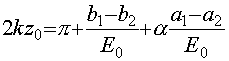 . (57)
. (57)
Снова используя выражение (24) с полем вида
![]() ,
,
получим для поля излучения, уходящего вправо
![]() . (58)
. (58)
Для поля излучения, уходящего влево от плоскости
![]() .
(59)
.
(59)
Поэтому для полного шума справа и слева от плоскости имеем, соответственно:
![]() . (60)
. (60)
Из выражения (60) следует, что квадратурные компоненты уходящего вправо и влево излучения коррелированы. Опять вводя новые квадратурные компоненты, как и в пункте 6, для минимальной спектральной плотности получим:
![]() . (61)
. (61)
Оптимизация выражения (61) по параметру
Следует, однако, отметить, что помимо корреляции квадратурных компонент отдельно для излучения, уходящего вправо, и для излучения, уходящего влево, из выражений (60) следует, что имеется также перекрестная корреляция квадратурных компонент. Для использования этой перекрестной корреляции необходимо смешать на дополнительном полупрозрачном зеркале волны, уходящие вправо и влево от плоскости,
причем для каждой волны надо выбрать соответствующую фазовую задержку. Пусть для определенности![]() (62)
(62)
Для спектральной плотности одной из квадратурных компонент имеем:
![]() . (63)
. (63)
В выражении (38) параметры
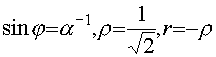 .
.
Тогда плотность квадратурной компоненты имеет асимптотику:
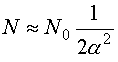 , (64)
, (64)
т. е. коэффициент сжатия неограниченно растет с ростом
9. Взаимодействие электронного слоя конечной толщины с плоской электромагнитной волной
Рассмотрим взаимодействие слоя конечной толщины
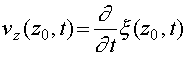 - его
продольная скорость, и
- его
продольная скорость, и 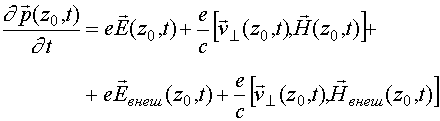 (65)
(65)
где
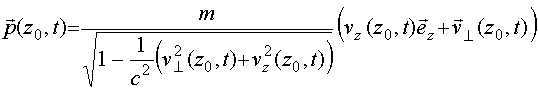 (66)
(66)
- релятивистский импульс электрона,
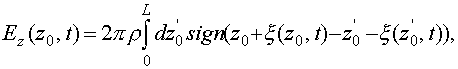
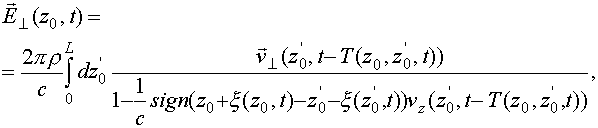
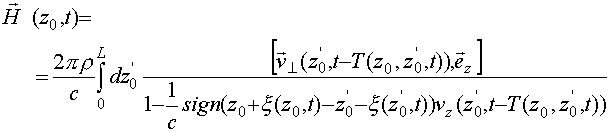 ,
(67)
,
(67)
![]()
![]() , (68)
, (68)
![]()
Система уравнений (65)-(68), дополненная начальными условиями, имеет единственное решение, описывающее эволюцию всего слоя. Уравнения (65)-(68) имеют довольно сложную структуру и, по-видимому, не допускают точного аналитического решения. Однако можно рассмотреть некоторые предельные случаи. Если мы, например, пренебрежем поперечными колебаниями электронов, полагая
Рассмотрим более подробно взаимодействие слоя электронов толщиной
L с плоской электромагнитной волной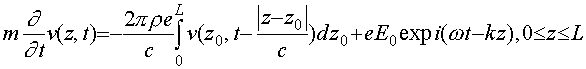 .(69)
.(69)
Выражение в правой части есть полное поле в точке
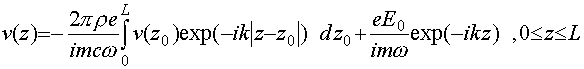 .(70)
.(70)
При его решении поступим следующим образом. Продифференцируем левую и правую части уравнения (70) по переменной
z и умножим их на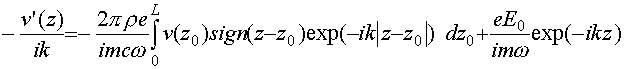 . (71)
. (71)
Складывая теперь (70) с (71), имеем:
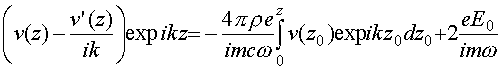
или после повторного дифференцирования по
z и приведения подобных слагаемых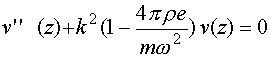 . (72)
. (72)
Общее решение уравнения (72) имеет вид
![]() ,
, ![]() , (73)
, (73)
где
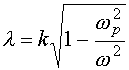 ,
, 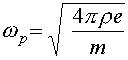 -плазменная
частота,
-плазменная
частота, 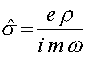 -комплексная
проводимость. Это решение представляет собой
сумму двух встречных волн с фазовыми скоростями
-комплексная
проводимость. Это решение представляет собой
сумму двух встречных волн с фазовыми скоростями 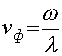 , в
соответствии с известными результатами [19]. Коэффициенты
, в
соответствии с известными результатами [19]. Коэффициенты Рассмотрим теперь взаимодействие слоя конечной толщины с плоской электромагнитной волной круговой поляризации в присутствии однородного магнитного поля
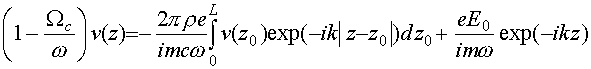 (74)
(74)
Его решение можно найти тем же методом, что и решение уравнения (70). В результате получим выражение (73) со следующим параметром
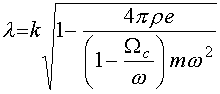 . (75)
. (75)
Проанализируем случай точного циклотронного резонанса
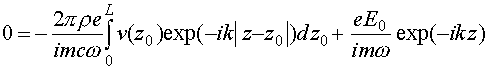 . (76)
. (76)
Можно показать, что уравнение (76) не имеет регулярных решений. Действительно, в точке циклотронного резонанса происходит полное отражение волны от листа с произвольной поверхностной плотностью
![]() . (77)
. (77)
Подставляя (77) в (76) и принимая
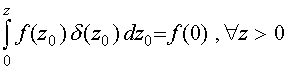 для
для 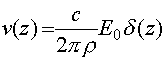 . (78)
. (78)
Разумеется, решение (78) имеет формальный характер в силу того, что время установления стационарного режима при резонансе будет стремиться к бесконечности. Заметим, что выражение (78) можно получить и непосредственно из (29), если формально полагать
Заключение
Полученные результаты могут быть использованы для многих электродинамических задач, имеющих допустимый тип симметрии среды и электромагнитного поля. Таковы, например, конфигурации, возникающие в теории лазеров на свободных электронах
[20], в задаче о генерации сжатых состояний электромагнитного поля [9,10], в теории отражения сверхмощной электромагнитной волны от плазменного слоя [21,22]. В последнем случае рассмотренная модель справедлива как для нормально, так и наклонно падающей волны. Для этого достаточно совершить переход в движущуюся систему отсчета, в которой тангенциальная компонента волнового вектора равна нулю [23].Следует отметить, что система уравнений (65)-(68) является полной (в рамках модели) и учитывает как кулоновские, так и радиационные процессы. В отличие от известных численных (3+1) - моделей
[22] в предлагаемой схеме решения самосогласованной задачи взаимодействия электронной среды и поля явно вычислены силы взаимодействия между листами, что позволяет рассматривать только уравнения движения и значительно сократить объем вычислений при численном моделировании.Кроме того, предлагаемая модель допускает сравнительно простые аналитические решения в виде ряда по степеням амплитуды внешнего поля. Так, в задаче о падении волны на плоский электронный слой (или среду с известным показателем преломления) в линейном приближении получаются известные классические решения
[19], а первая нелинейная поправка описывает генерацию третьей гармоники в отраженной и прошедшей волнах.Использование модели электронных листов в задачах генерации неклассических состояний электромагнитного поля показало, что сжатие электромагнитной волны при взаимодействии с электронной средой может быть существенным при высокой концентрации электронов. Однако, для пучков концентрация оказывается небольшой, поэтому для повышения коэффициента сжатия можно располагать несколько электронных зеркал друг за другом, или использовать резонаторные схемы.
Достоинством предложенной модели является также то, что она позволяет исследовать взаимодействие электромагнитной волны с электронной средой с учетом быстроосциллирующих членов на двойной частоте волны. В этом случае может быть реализован режим оптического вырожденного параметрического усилителя с большим коэффициентом сжатия выходного поля.
Литература
Авторы:
Ильин Антон Сергеевич,
Институт Радиотехники и Электроники Российской
Академии Наук,
e-mail: asi@mail.cplire.ru
Кулагин Виктор Владимирович,
Государственный Астрономический институт им. П.
К. Штернберга Московского государственного
университета им. М. В. Ломоносова,
e-mail: kul@sai.msu.su
Черепенин Владимир Алексеевич,
Институт Радиотехники и Электроники Российской
Академии Наук,
e-mail: cher@cplire.ru