Поверхностные волны над трапециевидно гофрированной поверхностью
Е .М. Арсеньева, В. А. Калошин
Институт
радиотехники и электроники им. В. А. Котельникова РАН
Получена 18 июня 2008 г.
В импедансном приближении получена формула для постоянной распространения поверхностной волны над трапециевидной гофрированной поверхностью. Проведено сопоставление результатов расчетов на основе полученной формулы с результатами численного эксперимента.
Известны работы, посвященные исследованию поверхностных волн в
гофрированных структурах с прямоугольной формой гофра [1,2]. Такие
гофрированные структуры применяются в электронике, волноводной и антенной
технике. Так, например, в круглом волноводе гофрировка стенок с глубиной гофра,
равные или несколько больше четверти длины волны позволяет уменьшить потери при
работе на основной волне ![]() или снять нежелательное вырождение
(совпадение фазовых скоростей) волн
или снять нежелательное вырождение
(совпадение фазовых скоростей) волн ![]() и
и ![]() в многомодовом волноводе. При глубине
гофра меньше, чем четверть длины волны над поверхностью распространяются
замедленные электромагнитных волны, которые эффективно взаимодействуют с
электронным потоком [2]. Гофрированные структуры используются также для
формирования узконаправленного излучения в антеннах поверхностной волны [3].
в многомодовом волноводе. При глубине
гофра меньше, чем четверть длины волны над поверхностью распространяются
замедленные электромагнитных волны, которые эффективно взаимодействуют с
электронным потоком [2]. Гофрированные структуры используются также для
формирования узконаправленного излучения в антеннах поверхностной волны [3].
В данной работе исследуется гофрированная поверхность с трапециевидной формой гофра (рис.1). Цель - исследование влияния на дисперсионную характеристику поверхностной волны формы гофра, его периода и глубины. Для нахождения постоянной распространения поверхностной волны применяются два метода. Одним из них является аналитический подход, основанный на импедансном приближении, другим – численное моделирование на основе метода конечных элементов. В последнем методе весь объем решаемой задачи разбивается на множество малых конечных элементов в виде тетраэдров. В результате задача сводится к решению системы алгебраических уравнений.
Продольное сечение двумерной трапециевидной гофры изображено на рис.1.
Период гофры ![]() , ширина открытой части периода
равна
, ширина открытой части периода
равна ![]() при
при ![]() ,
высота гофры
,
высота гофры ![]() .
Обозначим
.
Обозначим ![]() .
.
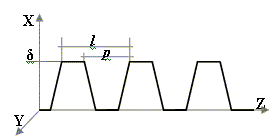
Рис.1 Трапециевидная гофрированная поверхность
Представим поле над
гофрой ( x> ![]() )в виде поверхностной волны:
)в виде поверхностной волны:
![]() ,
,
![]() (1)
(1)
![]() ,
,
где ![]() ,
,![]() - продольное и поперечное волновые числа, а
- продольное и поперечное волновые числа, а ![]() - волновой
вектор в свободном пространстве.
- волновой
вектор в свободном пространстве.
Проекция
электрического поля на ось ![]()
![]() пропорциональна проекции магнитного поля
на ось
пропорциональна проекции магнитного поля
на ось ![]()
![]() с коэффициентом
пропорциональности
с коэффициентом
пропорциональности ![]() (равным
величине импеданса), который не зависит от структуры внешнего поля:
(равным
величине импеданса), который не зависит от структуры внешнего поля:
![]() (2)
(2)
Далее будем полагать, что
внутри каждого периода гофры (при ![]() ) образуется основная стоячая волна
секториального рупора, поле которой в цилиндрических координатах можно записать
следующим образом:
) образуется основная стоячая волна
секториального рупора, поле которой в цилиндрических координатах можно записать
следующим образом:
|
|
(3) |
где ![]() и
и ![]() - функции Ханкеля первого и
второго порядка, соответственно,
- функции Ханкеля первого и
второго порядка, соответственно, ![]() - радиальная компонента в цилиндрической
системе координат (рис.2). Отношение коэффициентов
- радиальная компонента в цилиндрической
системе координат (рис.2). Отношение коэффициентов ![]() к
к ![]() можно определить из условия равенства нулю
тангенциальной компоненты поля
можно определить из условия равенства нулю
тангенциальной компоненты поля ![]() на металлической стенке при
на металлической стенке при ![]() , которое мы приближенно
заменим тем же условием (предполагая, что угол раствора рупора
, которое мы приближенно
заменим тем же условием (предполагая, что угол раствора рупора ![]() является малым) на
поверхности, образованной дугой окружности
является малым) на
поверхности, образованной дугой окружности ![]() , как показано на рис.2.
, как показано на рис.2.
Рассмотрим
один период этой гофры (рис.2). Используя граничное условие для
тангенциальной компоненты поля: ![]() при
при ![]() , находим связь между постоянными
, находим связь между постоянными ![]() и
и ![]() :
:
![]() (4)
(4)
Из уравнения (4) следует:
![]()
И формула (3) c учетом формулы (4) приобретает следующий вид:
![]() (5)
(5)
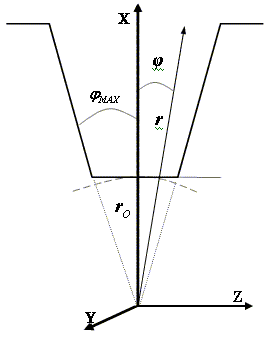
Рис.2 Один период трапециевидной гофры. Цилиндрические
координаты ![]() ,
,![]() ,
,![]() .
.
Запишем компоненты
электрического поля ![]() в цилиндрических координатах -
в цилиндрических координатах - ![]() ,
,![]() ,
,![]() (рис.2) через комплексные амплитуды
(рис.2) через комплексные амплитуды
![]()
![]()
![]() :
:
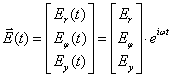 (6)
(6)
Для
нахождения проекции ![]() используем
уравнение Максвелла для комплексных амплитуд:
используем
уравнение Максвелла для комплексных амплитуд:
![]() (7)
(7)
В
цилиндрических координатах выражение для ротора электрического поля ![]() имеет следующий вид:
имеет следующий вид:
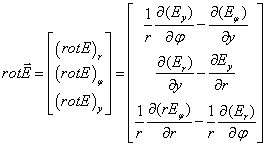 (8)
(8)
Учитывая (7) и (2), для проекции ![]() получаем следующее уравнение:
получаем следующее уравнение:
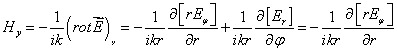
и, следовательно, зависимость
импеданса ![]() ,
который определяется из соотношения (2), от угла
,
который определяется из соотношения (2), от угла ![]() :
:
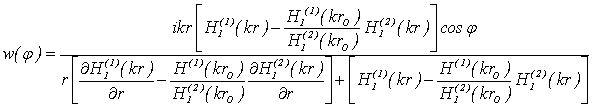 (9)
(9)
Переходя к пределу ![]() и учитывая, что
и учитывая, что
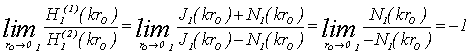
а также соотношение:
![]() ,
,
получим для зависимости импеданса ![]() от угла
от угла ![]() для треугольной гофры:
для треугольной гофры:
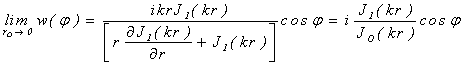
В декартовых координатах выражение
для импеданса ![]() на
поверхности
на
поверхности ![]() выражение
для импеданса
выражение
для импеданса ![]() будет
следующим:
будет
следующим:
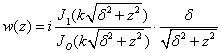
Далее введем
понятие среднего импеданса ![]() на открытой части гофры и понятие среднего
импеданса
на открытой части гофры и понятие среднего
импеданса ![]() на
периоде гофры
на
периоде гофры ![]() .
Очевидно, что средний импеданс на периоде
.
Очевидно, что средний импеданс на периоде ![]() будет отличаться множителем
будет отличаться множителем ![]() от среднего импеданса
на открытой части гофры
от среднего импеданса
на открытой части гофры ![]() :
:
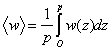 (10)
(10)
![]() (11)
(11)
Тогда, учитывая уравнение (8) для среднего импеданса на периоде треугольной гофры получим следующее уравнение:
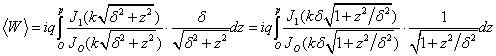 (12)
(12)
Общей формулой для среднего импеданса на периоде трапециевидной гофры будет следующее выражение, согласно формулам (10) и (11):
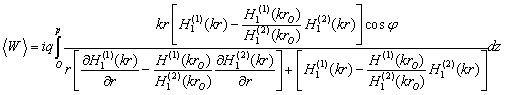 (13)
(13)
Рис.3
Треугольная гофра при ![]()
Далее будем рассматривать
треугольную гофру при ![]() (рис.3).
(рис.3).
Приравнивая
средний импеданс на периоде внутри гофры (формула (12)) импедансу поля вне
гофры (формула (2)) на границе гофры ![]() , получаем для величины
, получаем для величины ![]() в случае, когда
в случае, когда ![]() :
:
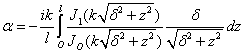 (14)
(14)
Тогда коэффициент замедления ![]() равен:
равен:
![]() ,
,
или, учитывая (9):
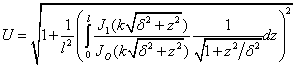 (15)
(15)
В общем виде, когда ![]() :
:
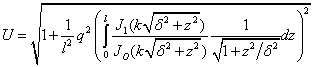 (16)
(16)
Рассмотрим узкий треугольный профиль, когда период l мал по сравнению с глубиной гофры δ:
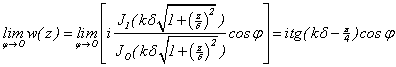
Для среднего значения импеданса получаем следующую формулу:
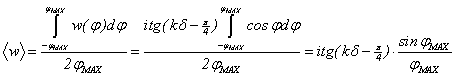 (17)
(17)
Или, переходя к пределу, ![]() , и учитывая, что
, и учитывая, что
![]() ,
,
получим для среднего импеданса выражение:
![]() (18)
(18)
Тогда для коэффициента замедления ![]() в
случае треугольной гофры получается следующая упрощенная формула:
в
случае треугольной гофры получается следующая упрощенная формула:
![]() (19)
(19)
Условием существования
поверхностной волны является требование ![]() . Следовательно, при
. Следовательно, при ![]() вдоль гофры
может распространяться замедленная волна.
вдоль гофры
может распространяться замедленная волна.
Для получения характеристик
медленной волны в прямоугольной бесконечной гофре на перейдем к пределу ![]() ,
, ![]() при
при ![]() для импеданса
для импеданса ![]() на поверхности
на поверхности ![]() , получаем следующее
выражение:
, получаем следующее
выражение:
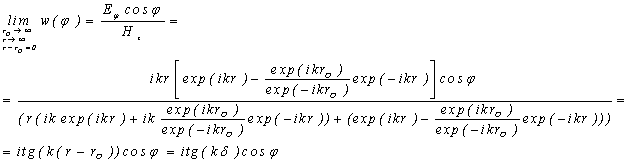
Коэффициент замедления ![]() прямоугольной
гофрированной поверхности будет равен:
прямоугольной
гофрированной поверхности будет равен:
![]() (20)
(20)
Отметим, что формула (20) совпадает с формулой, приведенной в [1].
Из формул (19) и (20) видно, что при одинаковых параметрах глубины ![]() ,
параметра
,
параметра ![]() коэффициент замедления
коэффициент замедления ![]() в
прямоугольной гофре больше. Коэффициент
замедления
в
прямоугольной гофре больше. Коэффициент
замедления ![]() больше 1, т.е. гофра обладает
замедляющими свойствами.
больше 1, т.е. гофра обладает
замедляющими свойствами.
Численное моделирование было основано на методе конечных элементов. Далее приведено сравнение численных и аналитических результатов для двумерных треугольной и прямоугольной гофрированных поверхностей.
На рис.4 и рис. 5 показано сравнение численных и аналитических значений коэффициента замедления, полученных для треугольной и прямоугольной гофры. Как видно, эти значения хорошо совпадают в большом диапазоне частот. На рис.4 штриховой линией показаны значения численного эксперимента, полученные для гофрированной поверхности конечной проводимости (медь).
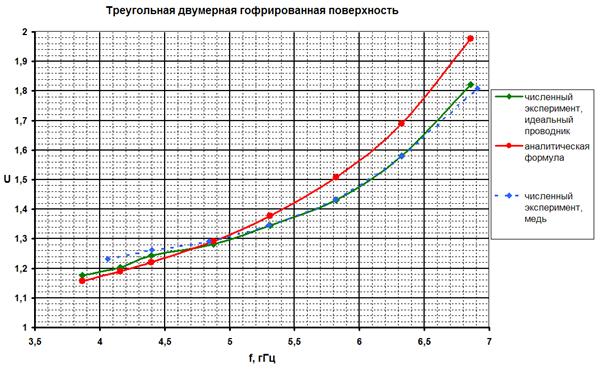
Рис.4 Сравнение
результатов, полученных численным экспериментом в программе HFSS 8 и использованием аналитической формулы (17). Глубина
гофры ![]() , период
, период
![]() ,
, ![]() .
.
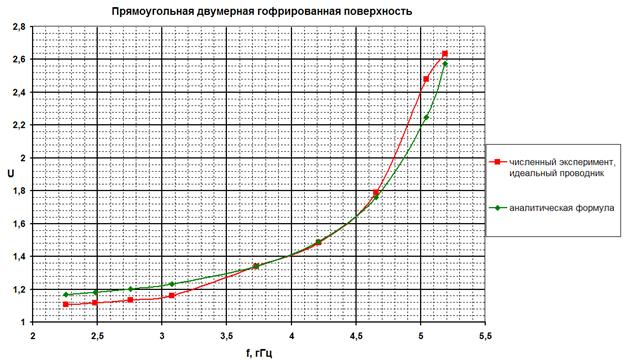
Рис.5 Сравнение
результатов, полученных численным экспериментом в программе HFSS 8 и использованием аналитической формулы (22). Глубина
гофры ![]() , период
, период
![]() ,
, ![]() .
.
В итоге,
· В работе получены аналитические формулы для расчета коэффициента замедления в трапециевидной гофрированной поверхности. В частном случае- случае прямоугольной гофрированной поверхности, полученные формулы совпадают с известными формулами, приведенными в литературе.
· Аналитически показано, что коэффициент замедления U для прямоугольного профиля гофра больше, чем для треугольного.
· Показано, что результаты расчета коэффициента замедления для двумерной гофрированной поверхности треугольного и прямоугольного профиля по аналитическим формулам хорошо совпадают с результатами численного исследования в большом диапазоне частот.
Список литературы
[1.] W. Rotman, “A study of Single-Surface Corrugated Guides,” Proc. IRE, 1951, vol. 39, Aug.,pp. 952-959.
[2.] Р.А.Силин, В.П. Сазонов ”Замедляющие системы”. Издательство “Советское радио”, 1966г.
[3.] Г.З. Айзенберг, В. Г. Ямпольский, О.Н.Терешин “Антенны УКВ”. ”Связь”, 1977 г.