| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 1999 |
Г.А. Ерохин, В.Г. Кочержевский
Московский Технический Университет Связи и
Информатики
Получена 5 марта 1999 г.
Установлено, что запасенная в окружающем пространстве энергия взаимодействия (разность средних значений взаимных электрических и магнитных энергий) поля излучения произвольной антенны и ее поля рассеяния целиком определяется характеристикой направленности этой антенны в передающем режиме. Полученные соотношения могут быть использованы для расчета взаимного импеданса двух антенн.
1. Проблема рассеяния электромагнитных волн, вызываемого антеннами, привлекает внимание в связи с необходимостью учета этого эффекта в задачах ЭМС, взаимодействия антенн и в других практических приложениях. Между тем, строгое решение задач рассеяния на реальных антеннах сопряжено с огромными трудностями. Поэтому вполне понятно стремление исследователей максимально использовать информацию о свойствах антенн в режиме излучения для нахождения характеристик рассеяния.
Разумеется, полную информацию о характеристиках рассеяния, зная только свойства антенн в передающем режиме, получить невозможно. До недавнего времени единственной такой характеристикой, определяемой через известную диаграмму направленности, была мощность, поглощаемая в процессе рассеяния в нагрузке антенны. Дополнительные возможности появились прежде всего благодаря установленной в [1,2] связи характеристик излучения и рассеяния антенн, получившей название антенной теоремы. Для произвольных металлических антенн,
не обладающих омическими потерями, расположенных в среде с параметрами
![]() справедливо
справедливо
(1) 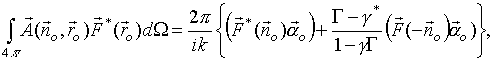
где
![]()
![]() ,
,
где
Левая часть антенной теоремы (1) представляет
собой, по существу, мощность взаимодействия поля
рассеяния антенны (практически никогда
неизвестного) и поля излучения этой же антенны в
передающем режиме. Указанная мощность,
переносимая через сферическую поверхность S
бесконечно большого радиуса, как показывает
правая часть (1), целиком определяется
характеристиками антенны в передающем режиме и
величиной коэффициента отражения
![]() .
.
Однако, как следует из теоремы Пойнтинга, взаимодействие двух полей в некоторой пространственной области V характеризуется не только мощностью взаимодействия, переносимой через границу S области V, но и энергией взаимодействия, заключенной в области V и определяемой как разность средних значений взаимных электрических и магнитных энергий.
Антенная теорема (1), как уже отмечалось, соответствует только первой из указанных характеристик взаимодействия. Целью данной работы является получение связи между второй характеристикой - энергией взаимодействия поля излучения и поля рассеяния, запасенной во всем окружающем пространстве, и ДН антенны в режиме излучения, которую полагаем известной.
2. Теоремой Пойнтинга энергия взаимодействия полей излучения и рассеяния определяется как
(2) 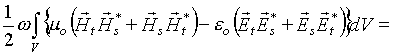
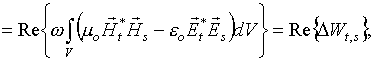
причем индексы
(3) ![]()
Введем обозначения:
(4) 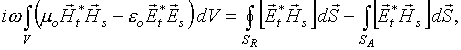
причем в (4) учтено, что для обеих поверхностей
В силу нулевых граничных условий для вектора
(5) 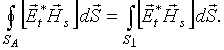
Представим вектор рассеянного поля
(6) 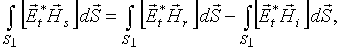
причем второй интеграл в правой части (6) целиком выражается через известные функции. Для вычисления первого интеграла используем полученное в [2] выражение для амплитуды электрического поля волны, распространяющейся в тракте (одномодовом) в сторону нагрузки в приемном режиме. При облучении антенны плоской волной с амплитудой
(7) 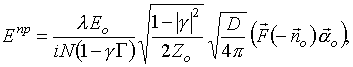
где ![]() - мощность бегущей волны в линии
питания при единичной амплитуде этой волны,
- мощность бегущей волны в линии
питания при единичной амплитуде этой волны, ![]() Ом,
Ом, ![]() -
коэффициент направленного действия (КНД) антенны
в направлении максимума излучения.
-
коэффициент направленного действия (КНД) антенны
в направлении максимума излучения.
Очевидно, полное поле в фидере (с учетом
отражения от нагрузки) в приемном режиме в
сечении ![]()
(8) ![]()
(9) 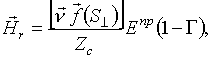
где
(10) ![]()
С учетом (9) и (10) для первого интеграла в правой части (6) получим
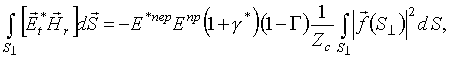
или, поскольку, согласно определению
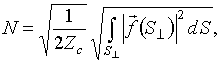
(11) 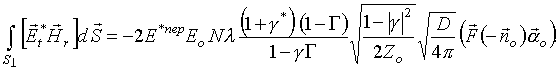
Вычислим теперь интеграл по поверхности
(12) 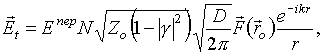
(13) 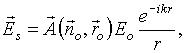
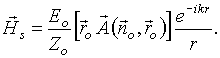
Поэтому
(15) 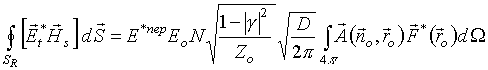
или, с учетом антенной теоремы (1)
(16) 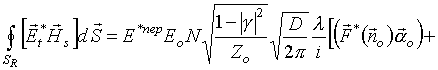
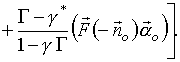
Подставляя (16) и (6) в (4), получим, с учетом (15), искомое выражение
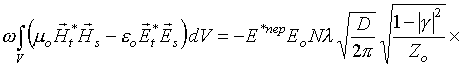
(17) 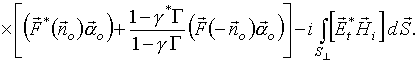
Соотношение (17), по аналогии с (1), назовем второй антенной теоремой. Обратим внимание, что разность средних значений взаимных энергий рассеянного и излученного полей, как и их взаимная мощность (1), целиком определяется свойствами антенны в передающем режиме и характеристиками облучающей волны.
Отметим, что иногда направленные свойства
антенны удобнее характеризовать через диаграмму
направленности ![]() с фазовой характеристикой,
определяемой через фазу входного тока
с фазовой характеристикой,
определяемой через фазу входного тока ![]() (а не фазу
падающей волны, как это было выше). Очевидно, что
функции
(а не фазу
падающей волны, как это было выше). Очевидно, что
функции ![]() и
и ![]() отличаются лишь постоянным фазовым
множителем:
отличаются лишь постоянным фазовым
множителем:
(18) ![]()
В частном случае, когда рассеянное поле порождается антенной с разомкнутым входом, т.е. при
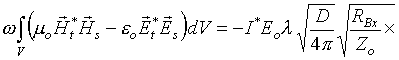
(19) 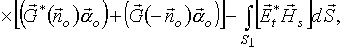
где
Полученные соотношения оказываются полезными, например, в теории взаимодействия антенн. В частности, вторая антенная теорема может быть использована при расчете реактивной составляющей взаимного импеданса
1 .СПИСОК ЛИТЕРАТУРЫ
1. Кинбер Б.Е., Попов М.П. // Докл. АН СССР. 1989. Т.308. N3. C. 615.
2. Ерохин Г.А., Кочержевский В.Г.// Радиотехника и электроника. 1997. Т.
42. N 1. C.86.3. Фельд Я.Н., Бененсон Л.С. Антенно-фидерные устройства. Ч.2. M. : ВВИА им. Н.Е. Жуковского, 1959.
4. Ерохин Г.А., Кочержевский В.Г. // Сб. Антенны / Под ред. Л.Д. Бахраха.- M.: ИПРЖР, 1998. Вып. 1 (40). C.9.
Авторы:
Ерохин Густав Арсентьевич
Кочержевский Вадим Георгиевич