| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9 , 2000 |
О ВОЗМОЖНОСТИ ЛАЗЕРНОГО УСКОРЕНИЯ ПЛОСКОГО СЛОЯ ЭЛЕКТРОНОВ
А.С.Ильин1, В.В.Кулагин2, В.А.Черепенин1
1Институт Радиотехники и Электроники РАН
2Государственный Астрономический институт им. П. К. Штернберга МГУ им. М. В. Ломоносова
Получена 31 августа 2000 г.
Рассмотрен процесс ускорения плотных электронных сгустков, получаемых, например, путем ионизации тонких пленок, мощными электромагнитными импульсами. Показано, что в этом случае определяющую роль играет сила реакции излучения сгустка. Релятивистский фактор в поле плоской волны растет пропорционально корню кубическому из времени взаимодействия. Для гауссовых пучков эффективное ускорение происходит на длинах порядка френелевской и ограничено мощностью импульса. Предложен метод ускорения электронного сгустка последовательностью гауссовых импульсов, не имеющий ограничений на максимальное значение энергии.
1. ВведениеВ последнее время большой интерес представляет проблема ускорения электронов в вакууме с помощью сверхмощных лазерных импульсов [1-8]. Обычно в задачах такого рода исследуется динамика движения одиночного электрона в поле мощной электромагнитной волны, при этом собственное излучение электрона в уравнениях движения не учитывается. В этом приближении оказывается справедливой теорема Лоусона-Вудворта [2], согласно которой в плоской волне электрон в среднем не ускоряется, именно, области ускорения сменяются областями замедления, и в среднем энергия электрона не растет. Аналогичный вывод можно сделать как в случае ограниченных пучков в пространстве (например, гауссовы пучки), так и во времени (мощные сверхкороткие импульсы): в среднем энергия электрона не увеличивается при взаимодействии с такими полями. Так, например, при взаимодействии со сверхкороткими импульсами электрон ускоряется передним фронтом импульса (происходит "выталкивание" электрона в область более слабого поля [1,2,4]), но затем энергия опять отбирается от электрона задним фронтом импульса, так что в итоге среднее вложение энергии оказывается близким к нулю. Такая же ситуация наблюдается и при взаимодействии с пространственно ограниченными пучками, имеющими конечный градиент поля. Существуют методы, позволяющие извлекать электрон из области взаимодействия при достижении им значительной энергии, основанные на боковом рассеянии электронов в пространственно неоднородном поле [1-6]. Однако, эти методы требуют значительной начальной энергии и, следовательно, предварительного ускорения электронов, кроме того, они не позволяют получать интенсивный поток ускоренных электронов с малым поперечным разбросом скоростей.
В последние годы появились методы получения плотных электронных сгустков путем ионизации твердых мишеней сверхкороткими лазерными импульсами [9]. Концентрация электронов в них практически равна концентрации в твердом теле, что требует использования новых подходов при описании процесса ускорения таких сгустков мощным лазерным полем в вакууме. Действительно, сила самодействия за счет собственного излучения сгустка может быть уже не малой, и должна учитываться при определении характера его движения. С учетом этой силы теорема Лоусона-Вудворта оказывается уже несправедливой [7], и электрон может ускоряться в среднем при взаимодействии с плоской волной.
В настоящем сообщении рассматривается один из вариантов ускорения плотного электронного сгустка, получаемого с помощью ионизации сверхмощным лазерным импульсом тонкопленочной мишени (толщиной значительно меньше длины волны) [9].
Рассмотрим вначале некоторые качественные соображения, относящиеся к учету коллективного радиационного взаимодействия электронов. Пусть на сгусток электронов объемом
Оценим величину этой силы по сравнению с обычной силой первого порядка по
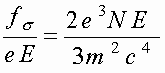 Оценка этого отношения для одного электрона в системе
Оценка этого отношения для одного электрона в системе Аналогичный вывод можно сделать и при сравнении средней силы обратной реакции излучения с градиентной пондеромоторной силой, рассматриваемой обычно в качестве основной при ускорении электронов электромагнитными импульсами в вакууме
[1-8]. Для этой силы имеем [4]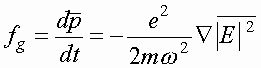 Здесь уже отношение сил не зависит от напряженности поля и составляет (в расчете на один электрон)
Здесь уже отношение сил не зависит от напряженности поля и составляет (в расчете на один электрон) 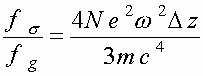 , где
, где Отметим, что задачи такого рода (включающие учет средней силы реакции собственного излучения системы) важны именно для сгустков электронов высокой плотности. Для традиционных электронных пучков с концентрацией электронов порядка
Приведенные выше качественные соображения показывают необходимость учета коллективных эффектов при ускорении плотных электронных сгустков. В общем случае точный учет силы реакции излучения в системе со многими релятивистскими электронами наталкивается на трудности принципиального характера
[10]. Численное моделирование требует одновременного решения уравнений Максвелла и релятивистских уравнений движения для многих электронов, что с одной стороны достаточно сложно, с другой, существенно затрудняет физическую интерпретацию получающихся результатов. Можно, однако, предложить модель, позволяющую в некоторых случаях аналитически получить выражения для силы обратной реакции излучения в случае многих электронов. Это так называемая 1D3V модель, когда движение электронов может быть описано одной пространственной координатой и тремя компонентами скорости. Оказывается, что для тонких пленок, ионизируемых мощными лазерными импульсами, именно эта модель наиболее адекватно описывает процессы в системе. 2. Модель и основные уравненияПусть среда однородна в направлениях,
перпендикулярных оси Oz , т. е. плотности заряда ![]() и тока
и тока ![]() зависят только от координаты z
и времени и , кроме того, положим:
зависят только от координаты z
и времени и , кроме того, положим: ![]() , где
, где ![]() - поверхностная плотность заряда, что физически соответствует тонкой заряженной плоскости, образованной бесконечно протяженным в x и y-направлениях слоем электронов, толщина которого значительно меньше длины волны падающего излучения. Формальные решения уравнений Максвелла в этом случае могут быть получены методом функции Грина и имеют вид [12]:
- поверхностная плотность заряда, что физически соответствует тонкой заряженной плоскости, образованной бесконечно протяженным в x и y-направлениях слоем электронов, толщина которого значительно меньше длины волны падающего излучения. Формальные решения уравнений Максвелла в этом случае могут быть получены методом функции Грина и имеют вид [12]:
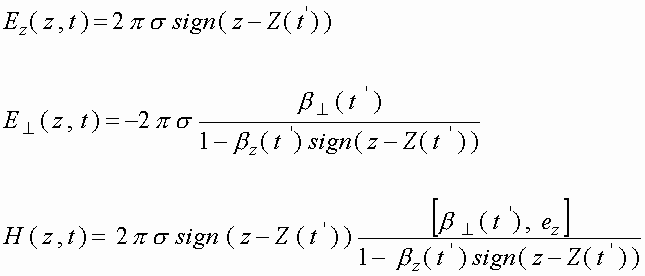 (1)
(1)
где
Заметим, что выражения (1) являются одномерными (или, точнее, 3+1- мерными) аналогами классических решений Лиенара – Вихерта
[10] и дают точное выражение для поля, создаваемого бесконечной плоскостью, при этом компонентуВзаимодействие электронов с самосогласованным полем излучения (1) приводит к появлению эффективной “вязкой”
силы, действующей на каждый электрон слоя [12,13]: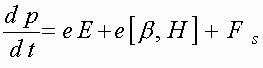 (2)
(2)
где
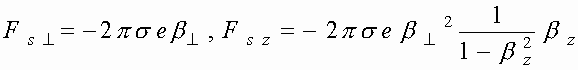 , а
, а Пусть теперь на электронный слой, расположенный в точке ![]() , падает плоская электромагнитная волна с волновым вектором
, падает плоская электромагнитная волна с волновым вектором ![]() , направленным вдоль оси Oz. Если не учитывать радиационных потерь (собственного излучения слоя), то движение зарядов происходит по замкнутой траектории, представляющей собой суперпозицию поперечных колебаний на частоте падающей волны и продольных колебаний на двойной частоте [10], т. е. средняя по периоду сила давления волны на слой оказывается равной нулю. Поэтому для корректного вычисления силы давления принципиально необходимо решать самосогласованную задачу.
, направленным вдоль оси Oz. Если не учитывать радиационных потерь (собственного излучения слоя), то движение зарядов происходит по замкнутой траектории, представляющей собой суперпозицию поперечных колебаний на частоте падающей волны и продольных колебаний на двойной частоте [10], т. е. средняя по периоду сила давления волны на слой оказывается равной нулю. Поэтому для корректного вычисления силы давления принципиально необходимо решать самосогласованную задачу.
Рассмотрим сначала нерелятивистские приближение ![]() . Из выражения
(2) для комплексной амплитуды скорости
. Из выражения
(2) для комплексной амплитуды скорости ![]() найдем:
найдем:
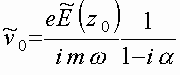 ,
где
,
где 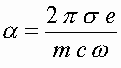 . Тогда для средней по периоду
. Тогда для средней по периоду ![]() силы Лоренца
силы Лоренца ![]() , действующей на один электрон, получим
, действующей на один электрон, получим
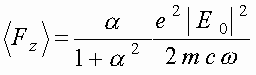 (3)
(3)
Выражение (3) имеет максимум при
Сила давления на единицу площади электронного слоя связана с силой давления на один электрон (3) соотношением
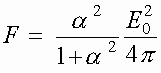 . Таким образом, сила давления на единицу площади максимальна при
. Таким образом, сила давления на единицу площади максимальна при Перейдем теперь к анализу релятивистских уравнений движения (2). Пусть плоская линейно поляризованная волна имеет компоненты
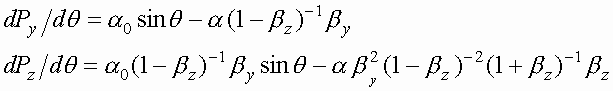 (4)
(4)
где ускорительный параметр
Исследуем асимптотическое поведение решения системы (4) для достаточно большого времени, когда продольная скорость
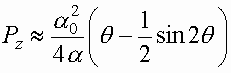 (5)
(5)
Таким образом, на больших временах релятивистский фактор
 (6)
(6)
Для релятивистского фактора
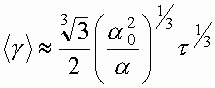 (7)
(7)
На рис. 1 показаны зависимости от фазы
полученного из численного решения уравнений
(4) с нулевыми начальными значениями координаты и скорости слоя для ![]() , т.е. при пренебрежении коллективными радиационными эффектами, и
, т.е. при пренебрежении коллективными радиационными эффектами, и ![]() . В последнем случае хорошее совпадение результатов с асимптотическим решением
(7) начинается уже при
. В последнем случае хорошее совпадение результатов с асимптотическим решением
(7) начинается уже при ![]() . Причем, в отличие от случая
. Причем, в отличие от случая ![]() , когда направление вектора скорости постоянно осциллирует, при
, когда направление вектора скорости постоянно осциллирует, при ![]() характер движения электронов качественно меняется: поперечная скорость электронов становится пренебрежимо малой, и вся их энергия определяется только продольным движением.
характер движения электронов качественно меняется: поперечная скорость электронов становится пренебрежимо малой, и вся их энергия определяется только продольным движением.
Как и следовало ожидать, корректный учет собственного излучения слоя привел к тому, что при ускорении плоской волной релятивистский фактор ![]() не ограничен и растет пропорционально фазе
не ограничен и растет пропорционально фазе ![]() . В лабораторной системе рост оказывается значительно более медленным и пропорционален только корню кубическому из времени. Существенным моментом здесь является также то, что сила обратной реакции излучения всегда приводит к ускорению слоя в отличие от градиентной силы
. В лабораторной системе рост оказывается значительно более медленным и пропорционален только корню кубическому из времени. Существенным моментом здесь является также то, что сила обратной реакции излучения всегда приводит к ускорению слоя в отличие от градиентной силы ![]() , которая может как ускорять электроны, так и замедлять их.
, которая может как ускорять электроны, так и замедлять их.
Большой интерес представляет анализ ускорения электронных сгустков не плоской волной, а реальными лазерными полями, получаемыми в экспериментах. Поле лазера обычно хорошо описывается низшей гауссовой модой, т. е. спадает при удалении от оси пучка и от фокуса [1,4]. Поэтому существует некая эффективная область взаимодействия, при выходе из которой электроны перестают ускоряться. Пусть поперечные размеры электронного слоя много меньше радиуса перетяжки гауссова пучка ![]() (в единицах
(в единицах![]() ). В этом случае можно пренебречь зависимостью амплитуды и фазы пучка от поперечных координат и считать их одинаковыми на протяжении электронного слоя. Пусть опять начальный продольный импульс слоя достаточно велик (энергия
). В этом случае можно пренебречь зависимостью амплитуды и фазы пучка от поперечных координат и считать их одинаковыми на протяжении электронного слоя. Пусть опять начальный продольный импульс слоя достаточно велик (энергия ![]() ). Тогда из уравнений
(4), учитывая, что теперь ускорительный параметр
). Тогда из уравнений
(4), учитывая, что теперь ускорительный параметр ![]() и фаза волны зависят от координаты слоя
и фаза волны зависят от координаты слоя ![]() , для релятивистского фактора найдем:
, для релятивистского фактора найдем:
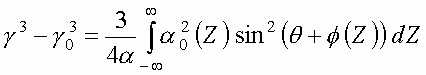 (8)
(8)
где
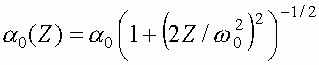 и
и 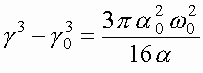 (9)
(9)
Изменение релятивистского фактора зависит только от мощности лазерного пучка
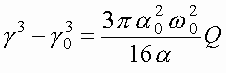 (10)
(10)
Таким образом, благодаря коллективным радиационным эффектам, в принципе возможен сколь угодно сильный разгон электронного слоя при взаимодействии не только с плоской электромагнитной волной (которая является в определенном смысле идеализацией), но также и с последовательностью мощных лазерных импульсов.
Подстановка характерных значений параметров
В заключение отметим, что рассмотренный механизм ускорения имеет особенно большое значение для сгустков электронов большой плотности и позволяет достигать больших значений энергии с малым разбросом поперечных скоростей.
Литература:1. F. V. Hartemann et. al. Phys. Rev. E, 51, N 5, 4833 (1995).
2. E. Esarey, P. Sprangle, J. Krall. Phys. Rev. E, 52, N 5, 5443 (1995).
3. G. Malka, E. Lefebvre, J. L. Miquel. Phys. Rev. Lett., 78, N 17, 3314 (1997).
4. B. Quesnel, P. Mora. Phys. Rev. E, 58, N 3, 3719 (1998).
5. L. J. Zhu et. al. Phys. Lett. A, 248, N 5, 319 (1998).
6. J. X. Wang et. al. Phys. Rev. E, 58, N 5, 6575 (1998).
7. A. L. Troha et. al. Phys. Rev. E, 60, N 1, 926 (1999).
8. Wei Yu et. al. Phys. Rev. E, 61, N 3, R2220 (2000).
. Р. В. Волков и др. Квантовая электроника, 24, N 12, 1114 (1997).10. Л. Д. Ландау, Е. М. Лифшиц. Теория поля. М.: Наука, 1988.
11. G. A. Mourou, C. P. J. Barty, and M. D. Perry, Phys. Today 51(1), 22 (1998).
13. V.L. Bratman, C.V. Samsonov, Phys. Lett. A, 206, 377 (1995).
Авторы: Ильин Антон Сергеевич,
e-mail: asi@mail.cplire.ru
Кулагин Виктор Владимирович, e-mail: kul@sai.msu.ru
Черепенин Владимир Алексеевич

