| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9 , 2000 |
ПОЛЕ ПОПЕРЕЧНОГО ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ, РАСПОЛОЖЕННОГО ВБЛИЗИ ИМПЕДАНСНОГО КРУГОВОГО ЦИЛИНДРА
М.Ю.
Звездина
Ростовский
военный институт ракетных войск
Получена 7 сентября 2000 г.
Приводятся соотношения для вычисления поля поперечного электрического диполя, расположенного вблизи импедансного кругового цилиндра. Анализируются закономерности распределения поля в ближней и дальней зонах для случаев поверхности кругового цилиндра с изотропным и анизотропным импедансом.
Как известно, на характеристики излучения электрических и магнитных диполей, расположенных вблизи импедансных круговых поверхностей, большое влияние оказывают поля в ближней зоне, поскольку они определяют распределение токов в излучающих элементах. Импедансные круговые поверхности с достаточной для практики точностью аппроксимируют широкий круг несущих конструкций реальных антенн, поэтому решение задачи о нахождении поля поперечного электрического диполя, расположенного вблизи импедансного кругового цилиндра, является интересным как в научном, так и в практическом плане [1].
Практической реализацией импедансных круговых структур могут служить [2-7] металлические цилиндры с конечной проводимостью, металлические цилиндры, покрытые тонким слоем диэлектрика, металлические цилиндры, окруженные тонким слоем плазмы, металлические цилиндры с гребенчатой структурой. Величина поверхностного импеданса, как показано в [3-7], определяется свойствами поверхности цилиндра и может либо зависеть, либо не зависеть от направления распространения электромагнитной волны (соответственно анизотропный и изотропный импеданс). Возбуждение импедансных поверхностей для ряда случаев рассмотрено в работах [2-4, 8-14]. Однако вопросы, связанные с влиянием поверхности кругового цилиндра с анизотропными импедансными свойствами на характеристики излучения поперечного электрического диполя, не нашли своего должного отражения.
В связи с вышесказанным целью работы является решение задачи о нахождении поля поперечного электрического диполя, расположенного вблизи импедансной поверхности кругового цилиндра.
Рассмотрим
однородный и безграничный вдоль оси ![]() круговой цилиндр радиуса
круговой цилиндр радиуса ![]() с тензором поверхностного импеданса
с тензором поверхностного импеданса ![]() ,
возбуждаемый поперечным электрическим
диполем (рис.1). Тензор
поверхностного импеданса
,
возбуждаемый поперечным электрическим
диполем (рис.1). Тензор
поверхностного импеданса ![]() ,
элементы которого зависят от параметров
поверхности цилиндра [3, 4],
может быть описан
соотношением
,
элементы которого зависят от параметров
поверхности цилиндра [3, 4],
может быть описан
соотношением 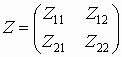 .
Ток в диполе с длиной плеча
.
Ток в диполе с длиной плеча ![]() и амплитудой
и амплитудой ![]() определяется выражением
определяется выражением
где ![]() - точка расположения центра диполя в
цилиндрической системе координат.
- точка расположения центра диполя в
цилиндрической системе координат.
Падающее
поле представим, как и в [3],
в виде бесконечного спектра цилиндрических
волн, распространяющихся в радиальном
направлении и модулированных по оси 0z.
Поскольку сторонний источник тока имеет
поперечную составляющую электрического
поля (диполь ориентирован вдоль орта ![]() ),
то в падающем поле присутствуют как
продольные, так и поперечные компоненты
электрического и магнитного полей
),
то в падающем поле присутствуют как
продольные, так и поперечные компоненты
электрического и магнитного полей
где ![]() ;
;
![]() ;
; ![]() - радиус-вектор произвольной точки P;
i – мнимая единица.
Множитель
- радиус-вектор произвольной точки P;
i – мнимая единица.
Множитель ![]() ,
описывающий зависимость всех величин от
времени, здесь и далее
опущен.
,
описывающий зависимость всех величин от
времени, здесь и далее
опущен.
Поскольку
выражения, описывающие продольные
компоненты в падающей электромагнитной
волне для случаев ![]() '
(поле в ближней зоне) и
'
(поле в ближней зоне) и ![]() (поле в дальней зоне), имеют различный вид [3],
приведем их позже. Поперечные компоненты
электромагнитного поля могут быть выражены
через продольные компоненты с
использованием соотношений [3]:
(поле в дальней зоне), имеют различный вид [3],
приведем их позже. Поперечные компоненты
электромагнитного поля могут быть выражены
через продольные компоненты с
использованием соотношений [3]:
В
соотношениях (3) ![]() - волновое число;
- волновое число; ![]() - длина волны;
- длина волны; ![]() Ом – волновое сопротивление свободного
пространства;
Ом – волновое сопротивление свободного
пространства; ![]() .
.
Поскольку
электродинамические и геометрические
параметры цилиндра не зависят от
координаты ![]() ,
решение задачи будем искать в
предположении, что рассеянное поле имеет
такую же зависимость от данной координаты,
как и в падающем поле:
,
решение задачи будем искать в
предположении, что рассеянное поле имеет
такую же зависимость от данной координаты,
как и в падающем поле:
где 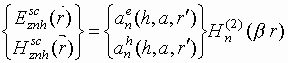 .
.
Поперечные
компоненты рассеянного поля могут быть
найдены с использованием соотношений (3)
при замене ![]() на
на ![]() и
и ![]() на
на ![]() .
.
Коэффициенты
![]() ,
описывающие дифракцию волны на импедансном
круговом цилиндре, определяются из
граничных условий
,
описывающие дифракцию волны на импедансном
круговом цилиндре, определяются из
граничных условий ![]() [3, 8]:
[3, 8]:
При
условиях, приведенных в [3, 8],
в соотношениях (5) можно положить ![]() и записать граничные условия в виде
и записать граничные условия в виде
где ![]() .
.
Используя соотношения (2)-(4), (6) несложно получить выражения для коэффициентов дифракции:
 ,
,
где
![]() ,
,
![]() - нормированный поверхностный импеданс для E-
и H-волн [3].
- нормированный поверхностный импеданс для E-
и H-волн [3].
Конкретизируем
выражения для коэффициентов дифракции ![]() для различных случаев удалений поперечного
диполя от поверхности кругового цилиндра.
для различных случаев удалений поперечного
диполя от поверхности кругового цилиндра.
При расположении поперечного электрического диполя вблизи импедансного кругового цилиндра продольные компоненты в падающем электромагнитном поле описываются выражениями [3]:
в которых
![]() - функция Бесселя n-го
порядка;
- функция Бесселя n-го
порядка; ![]() функция Ганкеля 2-го рода n-го
порядка.
функция Ганкеля 2-го рода n-го
порядка.
Коэффициенты дифракции – соотношения (7)-(12) - при этом принимают вид:
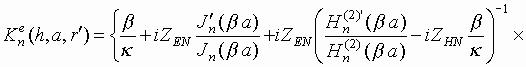 (16)
(16)
 ,
,
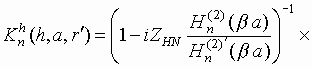 (17)
(17)
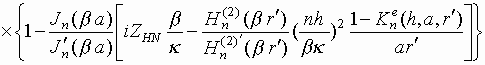 .
.
При
удалении поперечного электрического
диполя на бесконечность (![]() )
коэффициенты дифракции будут
соответствовать случаю падения плоской H-поляризованной
волны, поскольку, как показывает анализ
выражения (13), при
)
коэффициенты дифракции будут
соответствовать случаю падения плоской H-поляризованной
волны, поскольку, как показывает анализ
выражения (13), при ![]()
![]() .
Используя асимптотику функции Ганкеля для
больших значений аргумента
.
Используя асимптотику функции Ганкеля для
больших значений аргумента
запишем выражения для коэффициентов дифракции в виде, зависящем только от продольной компоненты магнитного поля:
 .
.
Полученные выражения совпадают с соотношениями, приведенными в [15] для случая падения плоской H-поляризованной волны на круговой импедансный цилиндр.
Запишем
компоненты электромагнитного поля,
возбуждаемого в точке P
поперечным электрическим диполем,
расположенным вблизи бесконечного
импедансного кругового цилиндра (в точке Q),
в случае ![]() (поле в ближней зоне):
(поле в ближней зоне):
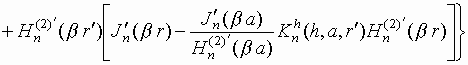 ,
(24)
,
(24)
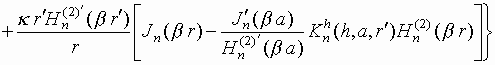 ,
,
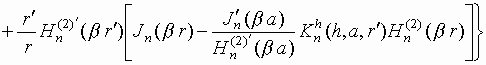 ,
(27)
,
(27)
Рассмотрим
случай ![]() (поле в дальней зоне). При этом продольные
компоненты в падающем поле описываются
выражениями [3]:
(поле в дальней зоне). При этом продольные
компоненты в падающем поле описываются
выражениями [3]:
Полное поле для
каждой компоненты, как было показано в [2,
3], получается при
устремлении ![]() .
При этом в подынтегральных выражениях (2),
(4) вместо функции Ганкеля берется
первый член ее асимптотического разложения
– соотношение (18). К получившимся
интегралам применим метод перевала,
подробно описанный в [3].
Переходя по формуле
.
При этом в подынтегральных выражениях (2),
(4) вместо функции Ганкеля берется
первый член ее асимптотического разложения
– соотношение (18). К получившимся
интегралам применим метод перевала,
подробно описанный в [3].
Переходя по формуле ![]() к новой переменной интегрирования
к новой переменной интегрирования ![]() ,
которую можно рассматривать как угол,
образуемый направлением.
,
которую можно рассматривать как угол,
образуемый направлением.
распространения
плоской волны с осью ![]() ,
и заменяя первоначальный путь
интегрирования в путь «наискорейшего
спуска», определяемый уравнением
,
и заменяя первоначальный путь
интегрирования в путь «наискорейшего
спуска», определяемый уравнением ![]() (x изменяется от
(x изменяется от ![]() до
до ![]() ;
; ![]() - первоначальная точка интеграла, в которой
фаза подынтегрального выражения
стационарна), несложно записать выражения
для компонент электромагнитного поля в
дальней зоне:
- первоначальная точка интеграла, в которой
фаза подынтегрального выражения
стационарна), несложно записать выражения
для компонент электромагнитного поля в
дальней зоне:
 ,
,
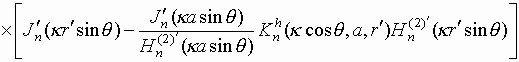 ,
,
 ,
,
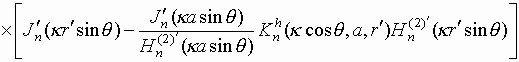 ,
,
 ,
,
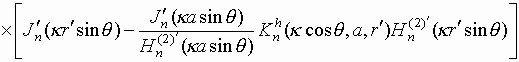 .
.
В
соотношениях (30)-(35)  - числа Неймана.
- числа Неймана.
В частном
случае идеально проводящего цилиндра (![]() )
множители
)
множители ![]() и
и ![]() ,
входящие в коэффициенты дифракции, равны
единице, а выражения (30)-(35)
полностью совпадают с соотношениями,
приведенными в [2, 3].
,
входящие в коэффициенты дифракции, равны
единице, а выражения (30)-(35)
полностью совпадают с соотношениями,
приведенными в [2, 3].
Представляет
интерес анализ влияния параметров
поверхностного импеданса на распределение
компонент электромагнитного поля. Так, в
случае продольной ребристой структуры ![]() [3]. При данном
значении импеданса коэффициенты
[3]. При данном
значении импеданса коэффициенты ![]() и
и ![]() определяются зависимостями
определяются зависимостями
т.е. для
продольной компоненты электрического поля
поверхность является идеально проводящей,
а ее импедансные свойства, связанные с
элементом тензора ![]() ,
проявляются только по отношению к
продольной компоненте магнитного поля. Для
поперечной ребристой структуры
,
проявляются только по отношению к
продольной компоненте магнитного поля. Для
поперечной ребристой структуры ![]() [16]. При этом ни
один из коэффициентов
[16]. При этом ни
один из коэффициентов ![]() и
и ![]() не обращается в единицу и импедансные
свойства поверхности проявляются для
продольных компонент как электрического,
так и магнитного полей.
не обращается в единицу и импедансные
свойства поверхности проявляются для
продольных компонент как электрического,
так и магнитного полей.
Таким образом, приведенные в статье соотношения являются формальным решением задачи о нахождении поля поперечного диполя, расположенного вблизи импедансного кругового цилиндра. Выражения, описывающие коэффициенты дифракции, позволяют исследовать случаи как изотропного, так и анизотропного поверхностного импеданса.
Литература
Автор:
Звездина
Марина Юрьевна – к.т.н., РВИ РВ, e-mail: zvezd@jeo.ru