|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2002 |
|
ВЫЧИСЛЕНИЕ ВЗАИМНОЙ СВЯЗИ КРЕСТООБРАЗНЫХ ВИБРАТОРОВ
В ПРИСУТСТВИИ ИМПЕДАНСНОГО КРУГОВОГО ЦИЛИНДРА
Звездина М.Ю. , e-mail: zvezd@jeo.ru
Ростовский военный институт ракетных войск
Получена 17 января 2002 г.
Широкое применение в малоэлементных антенных решетках крестообразных электрических вибраторов, а также нанесение импедансных покрытий на несущую конструкцию антенны делает актуальной задачу исследования влияния импедансных свойств покрытия на характеристики антенны, в том числе и на взаимную связь излучателей в составе излучающего раскрыва [1, 2]. При моделировании данного физического явления одним из важных вопросов является выбор способа аппроксимации распределения токов в вибраторах, поскольку от этого зависят как точность получаемых результатов, так и объем вычислений. Предполагая, что вибратор является тонким, при описании закона распределения тока вдоль него используются различные способы аппроксимации [3-6]: синусоидальное, полиномиальное, тригонометрическими гармониками Кинга, набором кусочно-постоянных функций и др. Однако в случае применения несущей конструкции в виде кругового цилиндра часто используются многомодовые антенны [6], распределение тока в которых может быть описано выражением:
где N
– число элементов антенной решетки; i
– мнимая единица;
![]() ‑
номер моды тока;
‑
номер моды тока;
![]() ‑
угловое положение n-го
излучателя (
‑
угловое положение n-го
излучателя (![]() ).
).
Несмотря на то, что вопросу исследования собственных и взаимных сопротивлений различным образом ориентированных вибраторов, размещенных вблизи кругового цилиндра, посвящено достаточно большое число работ (например, [2,7-9]), случай многомодового возбуждения крестообразных излучателей в присутствии несущей конструкции с импедансными свойствами изучен недостаточно полно. Таким образом, исследование собственных и взаимных сопротивлений крестообразных вибраторов в присутствии импедансного кругового цилиндра представляет несомненный научный и практический интерес.
Пусть вблизи импедансного кругового цилиндра радиуса
![]() с
тензором поверхностного импеданса
с
тензором поверхностного импеданса
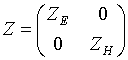 расположена
решетка
расположена
решетка
![]() идентичных
крестообразных излучателей, образованных продольными и поперечными
электрическими вибраторами с длиной плеча
идентичных
крестообразных излучателей, образованных продольными и поперечными
электрическими вибраторами с длиной плеча
![]() .
Центр n-го
излучателя (
.
Центр n-го
излучателя (![]() )
в цилиндрической системе координат
)
в цилиндрической системе координат
![]() определяется
координатами
определяется
координатами
![]() .
.
Для вычисления
коэффициентов взаимной связи n-го
и m-го
излучателей решетки (![]() )
воспользуемся методом наведенных эдс [7]:
)
воспользуемся методом наведенных эдс [7]:
в котором
![]() ‑
вектор распределения линейного тока в
n-м излучателе;
‑
вектор распределения линейного тока в
n-м излучателе;
![]() ‑
напряженность электрического поля, создаваемого
m-м излучателем на
n-м излучателе
в точке с радиус-вектором
‑
напряженность электрического поля, создаваемого
m-м излучателем на
n-м излучателе
в точке с радиус-вектором
![]() ;
;
![]() ‑
амплитуда тока в точке питания. Распределения токов (1) для
z- и
‑
амплитуда тока в точке питания. Распределения токов (1) для
z- и
![]() ориентированных
вибраторов n-го
крестообразного излучателя в предположении, что он является тонким, могут быть
записаны в виде:
ориентированных
вибраторов n-го
крестообразного излучателя в предположении, что он является тонким, могут быть
записаны в виде:
![]()
![]()
В соотношениях (3), (4)
приняты следующие обозначения:
![]() ‑
номер моды тока в плече вибратора с соответствующей ориентацией;
‑
номер моды тока в плече вибратора с соответствующей ориентацией;
![]() ‑
дельта-функция Дирака;
‑
дельта-функция Дирака;
![]() ;
;
![]() ‑
неизвестные комплексные амплитуды токов, определяемые из условия равенства
нулю тангенциальных составляющих электрического поля на поверхности
электрического вибратора. В предлагаемой постановке задачи электрическое поле
у поверхности вибраторов, образующих
n-й крестообразный излучатель, складывается из
поля подключенной к
‑
неизвестные комплексные амплитуды токов, определяемые из условия равенства
нулю тангенциальных составляющих электрического поля на поверхности
электрического вибратора. В предлагаемой постановке задачи электрическое поле
у поверхности вибраторов, образующих
n-й крестообразный излучатель, складывается из
поля подключенной к
![]() ориентированному
вибратору сторонней эдс
ориентированному
вибратору сторонней эдс
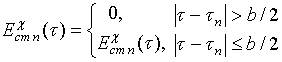 (где
(где
![]() ;
b –
ширина зазора между плечами вибраторов), поля, создаваемого в самом вибраторе,
и полей, порождаемых токами m-го
(
;
b –
ширина зазора между плечами вибраторов), поля, создаваемого в самом вибраторе,
и полей, порождаемых токами m-го
(![]() )
вибратора
)
вибратора
![]() .
.
Тангенциальные
компоненты электрического поля, создаваемого всеми составляющими токов у
поверхности z-
и
![]() ориентированных
вибраторов крестообразного излучателя, описываются соотношениями:
ориентированных
вибраторов крестообразного излучателя, описываются соотношениями:
В формулах (5) и (6)
электрические поля, порождаемые в точке с радиус-вектором
![]() на
n-м
вибраторе элементом тока m-го
вибратора, соответствующим точке с радиус-вектором
на
n-м
вибраторе элементом тока m-го
вибратора, соответствующим точке с радиус-вектором
![]() ,
обозначены для случая одинаковой ориентации излучателей как
,
обозначены для случая одинаковой ориентации излучателей как
![]() ,
в для ортогональной ориентации ‑
,
в для ортогональной ориентации ‑
![]() .
Выражения для
.
Выражения для
![]() -
компоненты поля крестообразного излучателя (
-
компоненты поля крестообразного излучателя (![]() )
с учетом результатов, приведенных в [8,10-14],
могут быть представлены в виде суперпозиции непрерывного и дискретного
спектров цилиндрических волн и для рассматриваемого случая импедансной
поверхности цилиндра имеют вид:
)
с учетом результатов, приведенных в [8,10-14],
могут быть представлены в виде суперпозиции непрерывного и дискретного
спектров цилиндрических волн и для рассматриваемого случая импедансной
поверхности цилиндра имеют вид:
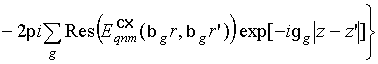 ,
,
где
![]() ‑
продольное волновое число; L
– контур интегрирования;
‑
продольное волновое число; L
– контур интегрирования;
![]() ‑
вычеты подынтегрального выражения, взятые в полюсах. Выбор контура
интегрирования, его деформации, а также нахождение полюсов подробно описано в
[14]. Спектральные компоненты электрического поля
z- и
‑
вычеты подынтегрального выражения, взятые в полюсах. Выбор контура
интегрирования, его деформации, а также нахождение полюсов подробно описано в
[14]. Спектральные компоненты электрического поля
z- и
![]() ориентированных
вибраторов определяются выражениями [10-14]:
ориентированных
вибраторов определяются выражениями [10-14]:
В соотношениях (8)-(10)
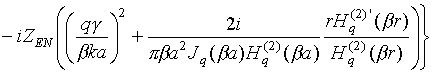 ,
,
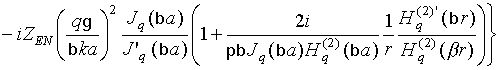 ,
,
где
![]() ‑
волновое число свободного пространства;
‑
волновое число свободного пространства;
![]() ‑
длина волны;
‑
длина волны;
![]() Ом;
Ом;
![]() ‑
соответственно функция Бесселя q-го
порядка и ее производная;
‑
соответственно функция Бесселя q-го
порядка и ее производная;
![]() ‑
функция Ганкеля q-го
порядка 2-го рода и ее производная соответственно;
‑
функция Ганкеля q-го
порядка 2-го рода и ее производная соответственно;![]() ‑ поперечное волновое число, связанное в предположении о малых потерях в
импедансной среде с продольным волновым числом
‑ поперечное волновое число, связанное в предположении о малых потерях в
импедансной среде с продольным волновым числом
![]() и
волновым числом свободного пространства
k соотношением
и
волновым числом свободного пространства
k соотношением
![]() ;
;
![]() ;
;
![]() .
.
Анализ соотношений (8)-(16)
показывает, что особые точки в представлении функции
![]() могут
возникнуть только в случае, когда знаменатель
D – выражение (16)
– обращается в нуль, поскольку, как показано в [15], в рассматриваемой
полуплоскости функция Ганкеля нулей не имеет.
могут
возникнуть только в случае, когда знаменатель
D – выражение (16)
– обращается в нуль, поскольку, как показано в [15], в рассматриваемой
полуплоскости функция Ганкеля нулей не имеет.
Комплексные амплитуды токов
![]() найдем
из решения интегрального уравнения относительно напряженности электрического
поля методом Галеркина. В качестве весовых используем тригонометрические
функции из представления распределения тока в вибраторах – соотношения (3)
и (4). Структура получаемой системы линейных алгебраических
уравнений вида
найдем
из решения интегрального уравнения относительно напряженности электрического
поля методом Галеркина. В качестве весовых используем тригонометрические
функции из представления распределения тока в вибраторах – соотношения (3)
и (4). Структура получаемой системы линейных алгебраических
уравнений вида
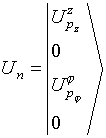
![]() является
блочной. При этом n-е
блоки вектора-столбца X
и вектора-столбца U
представляют собой соответственно искомые комплексные амплитуды мод
обобщенного тока в излучателях антенны и обобщенную стороннюю эдс
соответствующих мод тока в z-
и
является
блочной. При этом n-е
блоки вектора-столбца X
и вектора-столбца U
представляют собой соответственно искомые комплексные амплитуды мод
обобщенного тока в излучателях антенны и обобщенную стороннюю эдс
соответствующих мод тока в z-
и
![]() ориентированных
вибраторах
ориентированных
вибраторах
Коэффициенты матрицы Z
описывают коэффициенты взаимной связи мод обобщенного тока в излучающих
элементах антенны. Матрица является блочной, квадратной и имеет размер
![]() ,
где
,
где
![]() ‑
число учитываемых мод тока возбуждения в соответствующих вибраторах
крестообразного излучателя.
‑
число учитываемых мод тока возбуждения в соответствующих вибраторах
крестообразного излучателя.
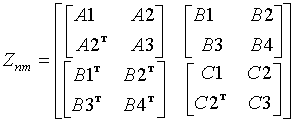
Рассмотрим более подробно структуру nm-го блока матрицы Z, описывающего связь n-го и m-го крестообразных излучателей на соответствующих модах тока. С учетом свойств симметрии и после выполнения преобразований, связанных с изменением порядка интегрирования, элементы данного блока могут быть представлены в виде
При этом блоки типа A
и C,
имеющие размеры
![]() и
и
![]() ,
описывают связь параллельных вибраторов (соответственно
z- и
,
описывают связь параллельных вибраторов (соответственно
z- и
![]() ориентированных),
а блоки типа B
(размер блока
ориентированных),
а блоки типа B
(размер блока
![]() )
– взаимно ортогональных вибраторов крестообразных излучателей; символ «т»
обозначает операцию транспонирования. Используя соотношения (2)-(17),
элементы данных блоков могут быть записаны в виде:
)
– взаимно ортогональных вибраторов крестообразных излучателей; символ «т»
обозначает операцию транспонирования. Используя соотношения (2)-(17),
элементы данных блоков могут быть записаны в виде:
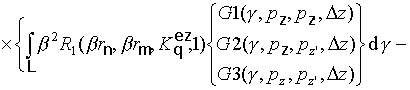
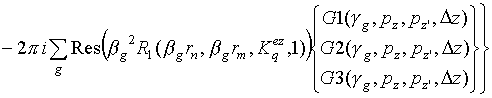 ,
,
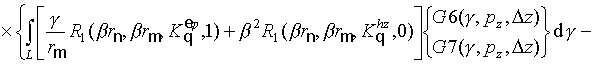
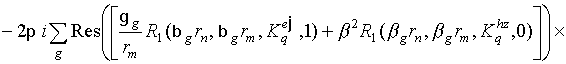
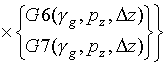 ,
,
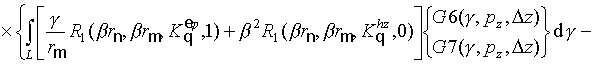
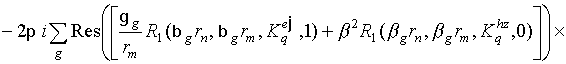
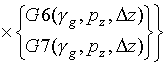 ,
,
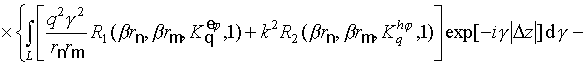
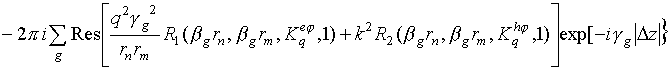 .
.
В соотношениях (20)-(23)
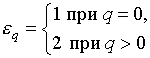 ‑
числа Неймана;
‑
числа Неймана;
![]() ;
;
![]() .
Интегралы
.
Интегралы
![]() могут
быть записаны в свернутой форме
[16]:
могут
быть записаны в свернутой форме
[16]:
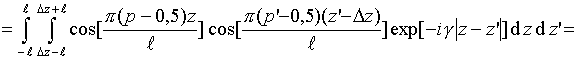
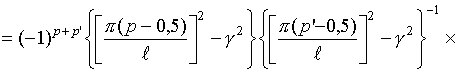
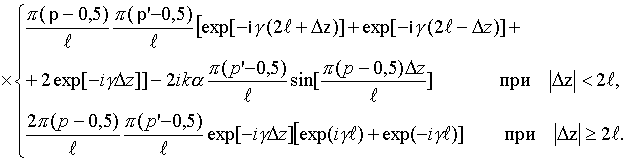
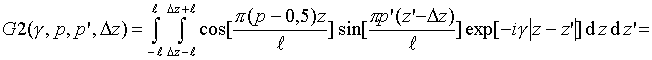
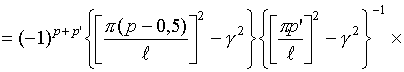
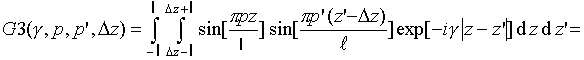
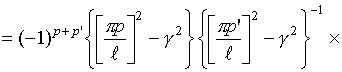
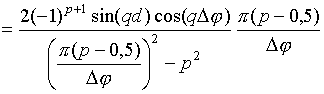 ;
;
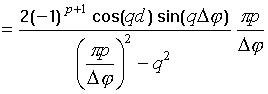 ;
;
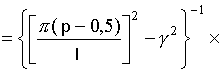
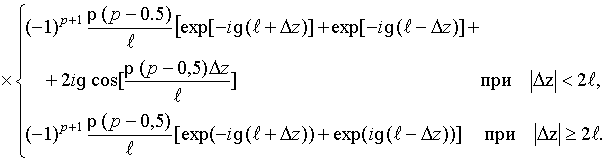
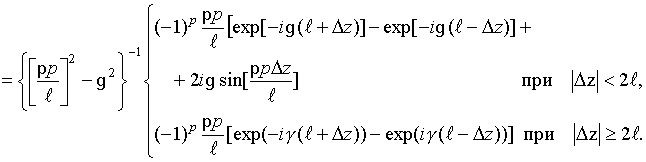
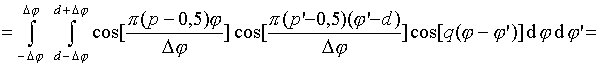
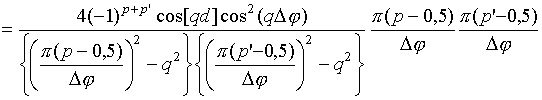 ;
;
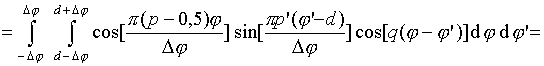
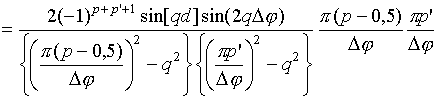 ;
;
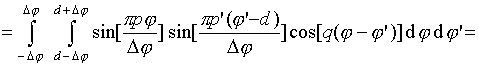
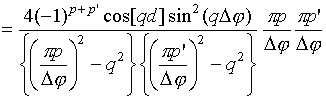 .
.
При построении вычислительного алгоритма интегралы
G1-G10целесообразно
использовать в приведенном выше виде, без дальнейших преобразований на основе
формул Эйлера. Данное обстоятельство обусловлено тем, что вычисляемый по
контуру L
интеграл, как показано в [9, 10,13-15],
после некоторых преобразований может быть представлен в виде суммы двух
интегралов – на отрезке [0,1] и на интервале
![]() .
На первом участке контура используются приведенные выше соотношения. Для
второго контура выражения легко получаются из исходных путем замены переменной
интегрирования
.
На первом участке контура используются приведенные выше соотношения. Для
второго контура выражения легко получаются из исходных путем замены переменной
интегрирования
![]() на
на
![]() .
.
Таким образом, приведенные соотношения позволяют вычислять коэффициенты взаимной связи электрических вибраторов, образующих крестообразные излучатели, расположенные вблизи импедансного кругового цилиндра, при описании распределения тока в вибраторах с использованием мод тока.
СПИСОК ЛИТЕРАТУРЫ
1. Проблемы антенной техники /Под ред. Л.Д. Бахраха, Д.И. Воскресенского. – М.: Радио и связь, 1989. – 368 с.
2. Евдокименко Ю.А., Зимин Д.Б., Косолапов И.И., Лосев В.С. О взаимосвязи крестообразных вибраторов в сканирующей антенне // Антенны. Вып.19. – М.: Связь, 1974. С.68-74.
3. Чаплин А.Ф., Бучацкий М.Д., Михайлов М.Ю. Синтез решеток пассивных вибраторов // Антенны. Вып.32. – М.: Связь, 1985. С.123-136.
4. Popovic B.D. Polynomial approximation of current along thin symmetrical cylindrical dipoles // Proc. IEE. 1970. V.117. №5. P.873-879.
5. King R.W.P., Mac R.B., Sander S.S. Arrays of cylindrical dipoles. – London: Cambridge University Press, 1966.
6. Носов Ю.Н. Минимизация числа излучателей слабонаправленных антенн // «Тр. ГосНИИрадио». 1991. №3. С.6-11.
7. Айзенберг Г.З., Ямпольский В.Г., Терешин О.Н. Антенны УКВ. Т.1. / Под ред. Г.З. Айзенберга. – М.: Радио и связь, 1989. – 384 с.
8. Gabriel’yan D.D., Zvezdina M.Yu. The calculation of mutual coupling between dipoles in presence of impedance circular cylinder // Proc. Of 3rd Int. Conf. Antenna Theory and Techniq., Sevastopil, Ukraine, 8-11 Sept. 1999, P.111-112.
9. Габриэльян Д.Д., Звездина М.Ю. Взаимные сопротивления продольных вибраторов вблизи импедансного кругового цилиндра // Радиотехника. 2000. №5. С.67-69.
10. Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Возбуждение кругового цилиндра с анизотропным импедансом продольным электрическим диполем // Радиотехника и электроника. 2001. Т.46. №8. С.875-879.
11. Звездина М.Ю. Поле поперечного электрического диполя, расположенного вблизи импедансного кругового цилиндра // Журнал радиоэлектроники. 2000. №9. http://jre.cplire.ru/win/sep00/2/text.html.
12. Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на поле поперечного диполя // Радиотехника и электроника. 2001. Т.46. №10. С.1126-1131.
13. Габриэльян Д.Д., Звездина М.Ю., Звездина Ю.А. и др. Возбуждение импедансной поверхности цилиндра поперечным электрическим диполем // Журнал радиоэлектроники. 2000. №10. http://jre.cplire.ru/win/oct00/6/text.html.
14. Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на поле произвольно ориентированного диполя // Журнал радиоэлектроники. 2001. №6. http://jre.cplire.ru/win/jun01/5/text.html.
15. Кравцов В.Г. Поле радиального электрического вибратора, расположенного вблизи идеально проводящего кругового цилиндра // Радиотехника. 1973. №8. С.43-50.
16. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. – М.: Наука, 1981. – 788 с.
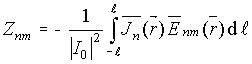 ,
(2)
,
(2)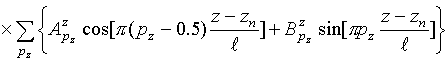 ,
(3)
,
(3)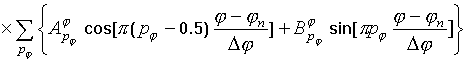 .
(4)
.
(4)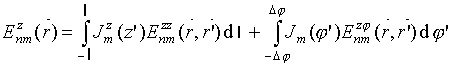 ,
(5)
,
(5)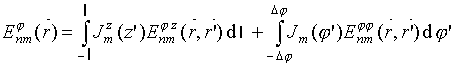 ,
(6)
,
(6)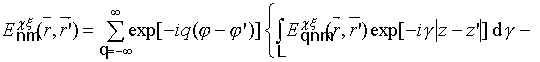 (7)
(7)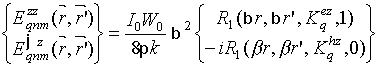 ,
(8)
,
(8)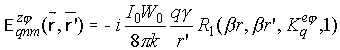 ,
(9)
,
(9)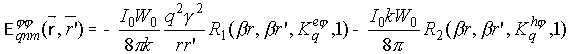 .
(10)
.
(10)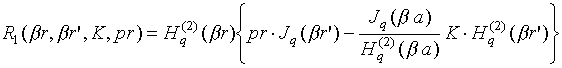 ,
(11)
,
(11)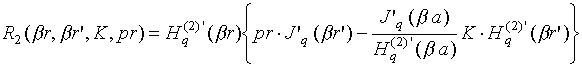 ,(12)
,(12) ,(13)
,(13)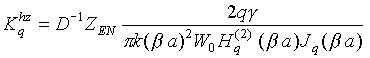 ,
(14)
,
(14)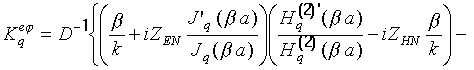 (15)
(15)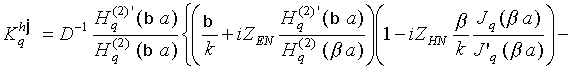 (16)
(16)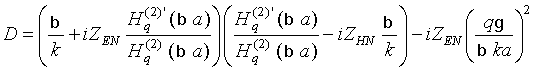 ,
(17)
,
(17)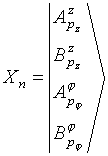 ,
,
 .
(18)
.
(18) .
(19)
.
(19)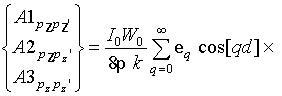 (20)
(20) (21)
(21)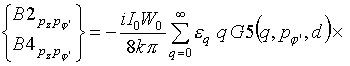 (22)
(22)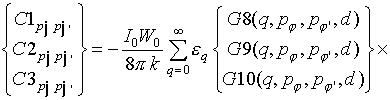 (23)
(23) (25)
(25)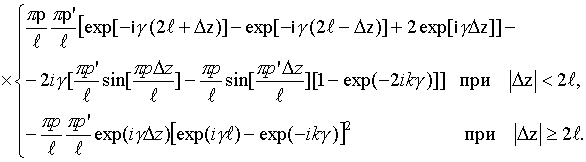 (26)
(26)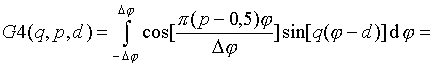 (27)
(27)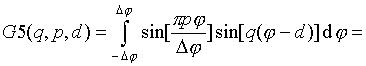 (28)
(28)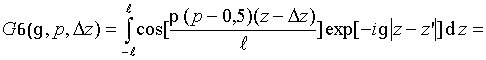 (29)
(29)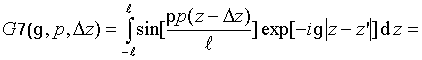 (30)
(30)