УДК: 621.372
Процесс нестационарного отражения коротких электромагнитных импульсов от многослойных фильтров с максимально плоской амплитудно-частотной характеристикой
А. В. Козарь, А. В. Трофимов, А. А. Потапов
Физический факультет МГУ имени М.В.Ломоносова
Статья поступила в редакцию 26 марта 2016 г.
Аннотация. В статье проводится исследование процесса нестационарного отражения короткого электромагнитного импульса от многослойного фильтра на основе двух полуволновых резонаторов с критической связью. Аналитически и численно было показано расщепление отраженного сигнала на четыре импульса вследствие нестационарного отражения; проведен анализ и сравнение полученных экспериментальных, аналитических и численных результатов. Показано, что определяющим фактором, влияющим на характер процесса нестационарного отражения короткого электромагнитного импульса от многослойной структуры, является функциональная зависимость коэффициента отражения многослойной структуры от частоты в окрестности несущей частоты падающего импульса. Теоретически продемонстрировано, что при отражении амплитудно-модулированного сигнала от фильтра с максимально плоской амплитудно-частотной характеристикой всегда существует момент времени, когда амплитуда отраженного сигнала стремится к нулю.
Ключевые слова: интерференция, многослойные интерференционные фильтры, нестационарное отражение, электромагнитный импульс.
Abstract: The process of the nonstationary reflection of a short electromagnetic pulse from the multilayer filter based on the two half-wave resonators with the critical coupling is investigated. Splitting of the signal to four pulses due to nonstationary reflection is shown analytically and numerically; experimental, analytical and numerical simulation results are analyzed and compared. It is shown that characteristics of the process of the nonstationary reflection of a short electromagnetic pulse are mostly determined by the multilayer structure’s reflection coefficient versus frequency dependency in the neighborhood of the carrier frequency. It is theoretically shown that in case of the reflection of an amplitude-modulated signal from the filter with the maximally flat frequency response, a moment of time when the amplitude of the reflected signal approaches zero does always exist.
Keywords: interference, multilayer interference filter, nonstationary reflection, electromagnetic impulse.
Введение
Электромагнитные импульсы малой длительности все чаще применяются как для научных исследований, так и в промышленности. Вопросы генерации, управления и детектирования таких импульсов в последнее десятилетие активно поднимаются в литературе [1-6]. Данная тенденция наблюдается как в микроволновом диапазоне, так и в оптическом. В первую очередь этому способствует появление источников коротких и сверхкоротких импульсов, создание сверхширокополосных приемников, а также интенсивное развитие оптического и микроволнового оборудования в целом. Под коротким электромагнитным импульсом, как правило, понимается импульс, длительность которого не превышает 100 периодов колебаний электромагнитного поля [5].
Для управления электромагнитными сигналами большой длительности широко применяются многослойные структуры, методы анализа и синтеза которых в настоящее время достаточно хорошо отработаны. Но практика применения многослойных структур для управления короткими импульсами выявила наличие целого ряда новых эффектов [1-6], что делает задачу исследования взаимодействия коротких и сверхкоротких электромагнитных импульсов с многослойными структурами весьма актуальной.
При взаимодействии электромагнитного сигнала с многослойной структурой в результате интерференции волн, отражённых от ее слоев, формируются прошедший и отраженный сигналы. При большой длительности падающего сигнала время установления стационарного процесса в многослойной структуре пренебрежимо мало по сравнению с длительностью сигнала и поэтому влияние нестационарного процесса на формирование отраженного и прошедшего сигналов не рассматривается.
В случае коротких импульсов длительность переходного процесса может стать сравнимой с длительностью сигнала. В таких случаях учет влияния нестационарного процесса в структуре на формирование отраженного и прошедшего сигналов становится необходимым.
Теоретические и экспериментальные исследования процесса нестационарного отражения, проведенные в [1-3], показали, что данное явление может эффективно использоваться при решении целого ряда прикладных задач: для генерации и диагностики коротких и сверхкоротких импульсов, при исследовании свойств материалов, для управления фазой сигнала; также были изучены особенности формирования отраженного сигнала, возникающие за счет дисперсии среды и потерь в ней.
Настоящая статья является продолжением начатых ранее исследований и посвящена анализу процесса нестационарного отражения импульсного сигнала от интерференционных многослойных фильтров.
2. Материалы и методы решения задачи и принятые допущения
Теоретический анализ. Рассмотрим процесс нестационарного отражения от однослойной интерференционной структуры фильтрующего класса, уединённого полуволнового слоя. Пусть на структуру подается электромагнитный импульс вида:
![]() ,
,
где ![]() – огибающая
импульса,
– огибающая
импульса, ![]() – частота
в герцах,
– частота
в герцах, ![]() – мнимая
единица. Как было
показано в работах [1-2], амплитуда огибающей отраженного сигнала в этом случае
может быть записана как:
– мнимая
единица. Как было
показано в работах [1-2], амплитуда огибающей отраженного сигнала в этом случае
может быть записана как:
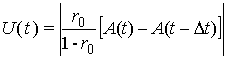 , (1)
, (1)
где ![]() – удвоенное время прохождения волны через слой. Предполагая,
что длительность падающего импульса T намного больше
– удвоенное время прохождения волны через слой. Предполагая,
что длительность падающего импульса T намного больше ![]() , несложно увидеть, что данное выражение с точностью
до коэффициента эквивалентно записи выражения для дифференциала функции
, несложно увидеть, что данное выражение с точностью
до коэффициента эквивалентно записи выражения для дифференциала функции ![]() . Разность
. Разность ![]() , входящая в (1), может принимать как положительное, так и
отрицательное значение. Разные знаки огибающей в области переднего и заднего
фронтов показывают, что импульсы отраженного сигнала находятся в противофазе.
, входящая в (1), может принимать как положительное, так и
отрицательное значение. Разные знаки огибающей в области переднего и заднего
фронтов показывают, что импульсы отраженного сигнала находятся в противофазе.
Падение короткого электромагнитного импульса без модуляции
фазы на структуру такого рода приведет к формированию сигнала с огибающей,
пропорциональной первой производной огибающей падающего импульса [1-3]. Из
выражения для модуля огибающей (1) видно, что отраженный сигнал будет состоять
из двух импульсов. Длительность отраженных импульсов будет соответствовать
длительности фронтов падающего сигнала, так как именно на фронтах ![]() .
.
Представляется интересным исследовать с практической и с фундаментальной точки зрения вопрос существования такой многослойной структуры, чтобы в процессе нестационарного отражения формировался сигнал с огибающей, пропорциональной второй производной огибающей падающего сигнала.
С этой целью рассмотрим следующую задачу: пусть на
многослойную структуру неотражающего типа падает короткий электромагнитный
импульс; необходимо определить, при какой функциональной зависимости
коэффициента отражения структуры ![]() от частоты, огибающая отраженного
сигнала будет пропорциональна второй производной от огибающей падающего сигнала.
от частоты, огибающая отраженного
сигнала будет пропорциональна второй производной от огибающей падающего сигнала.
Будем считать, что многослойная структура относится к
неотражающему типу, то есть ![]() . Также пусть спектр падающего импульса узкополосный
. Также пусть спектр падающего импульса узкополосный ![]() , где
, где ![]() – ширина спектра по уровню минус 3 дБ.
– ширина спектра по уровню минус 3 дБ.
Выразим амплитуду огибающей отраженного сигнала через спектр
падающего импульса ![]() и коэффициент отражения структуры
и коэффициент отражения структуры ![]() , применяя обратное преобразование Фурье. Для этого запишем в явном виде
выражение для спектра падающего сигнала:
, применяя обратное преобразование Фурье. Для этого запишем в явном виде
выражение для спектра падающего сигнала:
![]() .
.
Обозначим Фурье образ огибающей как:
![]() .
.
Тогда после несложных преобразований получаем что
![]() .
.
Исходя из постановки задачи, огибающая отраженного сигнала
пропорциональна второму дифференциалу от огибающей падающего сигнала. Тогда
получим уравнение для функции ![]()
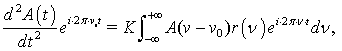
где ![]() – постоянная величина, не зависящая от частоты. Для удобства
дальнейших вычислений сделаем замену переменной
– постоянная величина, не зависящая от частоты. Для удобства
дальнейших вычислений сделаем замену переменной ![]() . Выполнив преобразования
окончательно получим уравнение:
. Выполнив преобразования
окончательно получим уравнение:
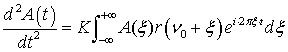
Так как падающий сигнал узкополосный и его спектр локализован
вблизи частоты ![]() , то точное значение коэффициента отражения
, то точное значение коэффициента отражения ![]() может быть заменено приближенным разложением в ряд по малому параметру
может быть заменено приближенным разложением в ряд по малому параметру ![]() , сходящемуся вблизи частоты
, сходящемуся вблизи частоты ![]() :
:
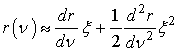 .
.
С учетом этого разложения окончательно получим:
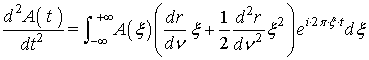 .
.
Данное уравнение имеет решение вида:
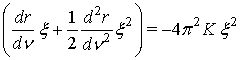 .
.
Условие, что огибающая отраженного сигнала есть производная от огибающей падающего сигнала, запишется в виде:
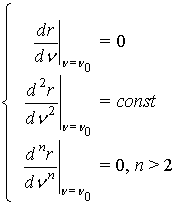 (2)
(2)
Другими словами, коэффициент отражения должен
иметь ноль второго порядка на частоте ![]() . Многослойные структуры
такого типа хорошо известны в литературе, посвященной вопросам синтеза фильтров
и просветляющих покрытий [7-9], и
являются полосовым фильтром второго порядка с максимально плоской амплитудно-частотной
характеристикой (АЧХ). Они встречаются как в оптике [9], так и в микроволновой
технике [8]. Особенность данного рода фильтров в том, что они оказывают
минимальное влияние на сигнал в полосе пропускания.
. Многослойные структуры
такого типа хорошо известны в литературе, посвященной вопросам синтеза фильтров
и просветляющих покрытий [7-9], и
являются полосовым фильтром второго порядка с максимально плоской амплитудно-частотной
характеристикой (АЧХ). Они встречаются как в оптике [9], так и в микроволновой
технике [8]. Особенность данного рода фильтров в том, что они оказывают
минимальное влияние на сигнал в полосе пропускания.
Теоретически могут быть синтезированы структуры с максимально плоской АЧХ и более высокого порядка. Повторяя аналогичные рассуждения, мы видим, что для того, чтобы огибающая отраженного сигнала была пропорциональна N-производной огибающей падающего сигнала, необходимо выполнение следующего условия: многослойная структура должна иметь на несущей частоте падающего импульса ноль коэффициента N-ого порядка.
Синтезировать структуру со строго нулевым коэффициентом отражения невозможно, поэтому огибающая отраженного сигнала будет приближенно соответствовать N-производной от огибающей падающего сигнала. Порядок нуля, который можно получить при практической реализации, ограничен доступной точностью изготовления структуры и величиной потерь в слоях структуры, поэтому в технике сверхвысоких частот структуры выше седьмого порядка встречаются крайне редко [8].
Простейшей реализацией многослойной структуры с максимально
плоской АЧХ является фильтр, состоящий из двух резонаторов, между которыми реализована
критическая связь [8,
10]. В оптическом диапазоне такого рода резонаторы
могут быть выполнены из диэлектрических пленок толщиной, кратной ![]() , окруженных брэгговскими зеркалами [11].
, окруженных брэгговскими зеркалами [11].
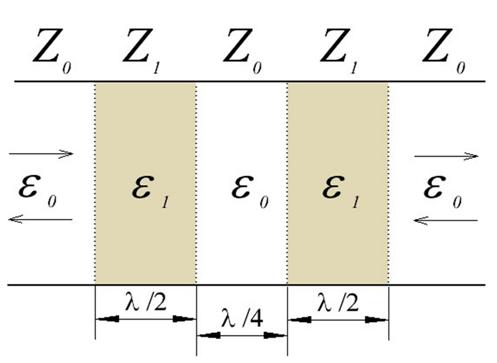
Рис. 1. Структура рассматриваемого трехслойного фильтра.
Рассмотрим структуру, состоящую из двух полуволновых слоев
с относительной
диэлектрической проницаемостью ![]() , которые расположены в свободном
пространстве друг за другом на расстоянии четверть длины волны (рис. 1). Будем считать, что
полуволновые слои изготовлены из диэлектрика без потерь. Предположим, что слои
имеют большие поперечные размеры относительно длины волны падающего сигнала и
дифракционными явлениями на их краях можно пренебречь. Пусть на структуру
падает плоская монохроматическая электромагнитная волна. Для анализа описанной трехслойной
структуры воспользуемся методом импедансных характеристик [12].
, которые расположены в свободном
пространстве друг за другом на расстоянии четверть длины волны (рис. 1). Будем считать, что
полуволновые слои изготовлены из диэлектрика без потерь. Предположим, что слои
имеют большие поперечные размеры относительно длины волны падающего сигнала и
дифракционными явлениями на их краях можно пренебречь. Пусть на структуру
падает плоская монохроматическая электромагнитная волна. Для анализа описанной трехслойной
структуры воспользуемся методом импедансных характеристик [12].
Для импедансов слоев можно записать: 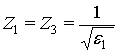 и
и
![]() . Поскольку потери в слоях
отсутствуют, импедансы слоев будут чисто действительными величинами.
. Поскольку потери в слоях
отсутствуют, импедансы слоев будут чисто действительными величинами.
Коэффициент отражения от исследуемой структуры будет рассчитываться из соотношения:
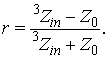
Величина ![]() может быть рассчитана с помощью рекуррентного
соотношения:
может быть рассчитана с помощью рекуррентного
соотношения:
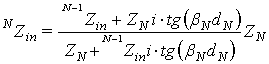 , (3)
, (3)
где индекс
N характеризует номер слоя, на границе
которого происходит расчет входного импеданса. Выражения для постоянной распространения волны ![]() имеют вид:
имеют вид:
![]() ,
,
с – скорость света в вакууме, ![]() – относительная диэлектрическая проницаемость слоя с номером N. Рассмотрим поведение коэффициента отражения вблизи частоты,
на которой слои являются
полуволновыми. Для удобства дальнейших вычислений сделаем замену переменной
– относительная диэлектрическая проницаемость слоя с номером N. Рассмотрим поведение коэффициента отражения вблизи частоты,
на которой слои являются
полуволновыми. Для удобства дальнейших вычислений сделаем замену переменной ![]()
Разложим в ряд входящие в соотношения (3) тангенсы. Для полуволнового слоя в окрестности ν0 будем иметь:
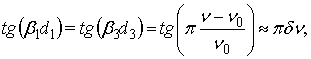
Для четвертьволнового слоя будем иметь:
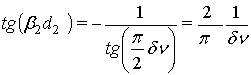 .
.
В результате расчет входного импеданса рассматриваемой системы сводится к решению последовательности рекуррентных соотношений:
Коэффициент отражения от структуры также может быть разложен в ряд по
степеням ![]() . После выполнения всех преобразований получим:
. После выполнения всех преобразований получим:
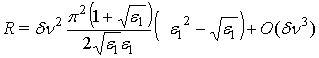 . (4)
. (4)
Из соотношения (4) видно, что член, пропорциональный ![]() отсутствует, а так как импульс
считаем узкополосным, то
отсутствует, а так как импульс
считаем узкополосным, то ![]() малый параметр и величиной
малый параметр и величиной ![]() можно пренебречь относительно
можно пренебречь относительно
![]() .
.
Таким образом, в окрестности частоты нулевого отражения
данная структура обладает коэффициентом отражения, пропорциональным квадрату
отстройки ![]() . Такое поведение коэффициента
отражения, как было показано выше, (формула (2)) необходимо для того, чтобы
огибающая сигнала, сформированного в результате нестационарного отражения, была
пропорциональна второй производной огибающей падающего импульса.
. Такое поведение коэффициента
отражения, как было показано выше, (формула (2)) необходимо для того, чтобы
огибающая сигнала, сформированного в результате нестационарного отражения, была
пропорциональна второй производной огибающей падающего импульса.
Можно показать, что рассмотренная структура с максимально плоской
амплитудно-частотной характеристикой также может быть синтезирована из слоев
кратных ![]() , разделенных слоем кратным
, разделенных слоем кратным ![]() .
.
Учет дисперсии и потерь. Нами была рассмотрена идеальная структура фильтра. При практической реализации многослойной структуры может возникнуть необходимость учета дополнительных физических явлений. Так, например, в условиях эксперимента в свободном пространстве может оказаться значительным явление дифракции на краях пластинок и отклонение формы фронта падающей волны от плоской. Кроме того, появятся дополнительные требования к точности позиционирования пластин и к их толщине. Не менее важным, как видно из работы [3], является необходимость учета реальных потерь в слоях многослойной структуры.
Схема практической реализации рассмотренного фильтра сильно зависит от частотного диапазона, для которого он применяется. Так в оптическом диапазоне при синтезе многослойных фильтров используют подложку, на которую последовательно напыляют слои. В этом случае при синтезе фильтра необходимо учитывать не только потери в слоях структуры, но и дисперсию материала, как слоев, так и подложки.
В микроволновом диапазоне длин волн подобного рода структуры могут быть реализованы в волноводе. В этом случае дополнительно необходимо учитывать влияние дисперсии волновода на коэффициент отражения. С другой стороны, решается проблема учета дифракции на краях пластинок и формы фронта падающей волны, так как пластинка полностью перекрывает сечение волновода.
В нашем случае изучалась модель волноводного фильтра как наиболее удобная для экспериментального исследования. Рассмотрим данную модель подробнее и проведем ее численный анализ с учетом волноводной дисперсии и потерь в слоях структуры.
Пусть слои установлены в свободном прямоугольном волноводе, в
котором возбуждена основная мода ![]() . Будем считать, что слои изготовлены
из диэлектрика с малыми потерями. Тогда выражение для относительной
диэлектрической проницаемости будет иметь вид
. Будем считать, что слои изготовлены
из диэлектрика с малыми потерями. Тогда выражение для относительной
диэлектрической проницаемости будет иметь вид ![]() [T1] , где
[T1] , где ![]() и
и ![]() – мнимая и действительная части
относительной диэлектрической проницаемости соответственно. Будем считать, что
потери в слоях структуры малы
– мнимая и действительная части
относительной диэлектрической проницаемости соответственно. Будем считать, что
потери в слоях структуры малы ![]() . С учетом волноводной дисперсии выражение для импедансов слоев и
свободного волновода имеет вид [3]:
. С учетом волноводной дисперсии выражение для импедансов слоев и
свободного волновода имеет вид [3]:
![]()
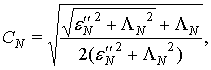
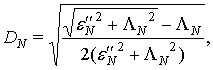
где 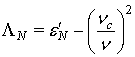 ,
, ![]() – критическая частота в волноводе для моды
– критическая частота в волноводе для моды ![]() ,
, ![]() – частота.
– частота.
Выражения для постоянной распространения волны γ имеют вид:
![]()
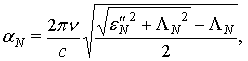
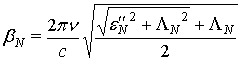 .
.
Рекуррентное соотношение метода импедансных характеристик для входного импеданса N-ого слоя будет иметь вид:
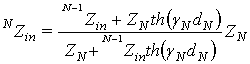 .
.
В работе [3] было показано, что потери в образце не влияют на
его оптическую толщину, в нашем случае – на резонансную частоту полуволнового слоя. Тогда для
расчета толщины слоев можно учитывать только дисперсию волновода. В этом случае
для расчета толщины слоев имеем:![]() , где
, где ![]() – реальная часть
импеданса слоя.
– реальная часть
импеданса слоя.
Анализ процесса нестационарного отражения требует перехода во
временную область. Для этого воспользуемся обратным преобразованием Фурье [13],
в результате чего получим, что огибающая отраженного сигнала ![]() может быть рассчитана из соотношения:
может быть рассчитана из соотношения:
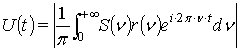
Интегрирование будем вести только по положительной частоте, поскольку нас интересует огибающая отраженного сигнала.
3. Результаты
Как показало численное моделирование методом импедансных характеристик, наличие потерь в слоях структуры приводит к появлению отраженного сигнала в области постоянной амплитуды падающего сигнала. На рис. 2 представлены результаты моделирования процесса нестационарного отражения электромагнитного импульса с трапецеидальной (а) и супергауссовой (б) огибающей от двухслойного фильтра при наличии и при отсутствии потерь в слоях. Дополнительно для наглядности на рисунках 2 и 3 показана огибающая падающего сигнала, уменьшенная уменьшенная по оси U в несколько десятков раз.

Рис. 2.
Численно рассчитанные огибающая отраженного сигнала,
для падающего импульса c
трапецеидальной огибающей (а) и
с супергауссовой огибающей (б) от двухслойного
фильтра
(I – без учета потерь; II – с учетом потерь, III – огибающая падающего
сигнала).
Как и ожидалось, для структуры без потерь отраженный сигнал состоит из серии уединенных импульсов. Четко заметно наличие четырех импульсов в отраженном сигнале, в отличие от двух импульсов в случае однослойной структуры [1-3]. Четыре импульса в отраженном сигнале, как видно из рис. 2, соответствуют четырем точкам максимума второй производной огибающей падающего импульса.
Также можно заметить, что при учете потерь в структуре появляется дополнительный отраженный сигнал, как в области постоянной амплитуды, так и в области линейного нарастания фронтов. В этом случае можно только приближенно считать, что огибающая отраженного сигнала является второй производной от огибающей падающего. Численное моделирование показывает, что при отражении электромагнитного импульса от фильтра с максимально плоской АЧХ с потерями всегда существует момент времени, когда амплитуда отраженного сигнала стремится к нулю. Из рис. 2 видно, что процесс нестационарного отражения от трехслойного фильтра с максимально плоской АЧХ существенно изменяет свой характер относительно однослойной системы [3].
Для экспериментальной проверки описанного явления
использовался полосовой фильтр, состоящий из двух волновых пластинок. В
качестве материала для изготовления пластинок был выбран фторопласт. Фторопласт
имеет малые потери в микроволновом диапазоне частот [14]. Пластинки были
установлены на расстоянии четверть длины волны друг от друга в прямоугольном
волноводе. Волновод имел прямоугольное сечение 23 х 10 мм.
Фильтр был настроен на частоту 8,4 ГГц и имел следующие геометрические
размеры: толщина фторопластовых пластинок - 30,0 мм, толщина воздушного
зазора между пластинками - 14,5 мм. Диэлектрическая проницаемость
фторопласта для данной частоты была предварительно измерена согласно методике,
описанной в работе [3], и составила ![]() .
.
Измерительный стенд состоял из векторного анализатора цепей Rohde&Schwarz ZNB‑20, к которому коаксиальным кабелем через коаксиально-волноводный переход (КВП) подключался отрезок прямоугольного волновода. Многослойный фильтр устанавливался посередине волновода, чтобы максимально снизить влияние щелевых волн на измеряемый коэффициент отражения. С противоположной стороны от КВП волновод нагружался на согласованную волноводную нагрузку. В ходе эксперимента измерялся комплексный коэффициент отражения от структуры. Для получения огибающей отраженного сигнала использовалось обратное преобразование Фурье. Данный процесс подробно описан в [3, 13].
В эксперименте на получаемые результаты оказывали влияние паразитные переотражения в волноведущей системе: отражения от фланцев волноводов, от возбуждающего штыря и т.п. Для исключения воздействия паразитных искажений на полученные результаты был применен метод фильтрации во временной области [13, 15].
4. Обсуждение полученных результатов
На рис. 3 представлен результат теоретического моделирования и экспериментально измеренные огибающие импульса, отраженного от исследуемой структуры. Как видно, результаты теоретического расчета хорошо согласуются с экспериментальными данными. Экспериментальные результаты показали, что в процессе нестационарного отражения электромагнитного импульса от трехслойного фильтра с максимально плоской АЧХ формируется четыре коротких импульса. Положения импульсов совпадают с максимумами производной огибающей падающего сигнала.
Сигнал, сформированный в процессе нестационарного отражения от рассмотренной структуры, принципиально отличается от сигнала, отраженного от однослойного фильтра. Как и в случае полуволнового фильтра, потери в слоях структуры оказывают существенное влияние на процесс нестационарного отражения. Также видно, что существует момент времени, когда амплитуда отраженного сигнала стремится к нулю.
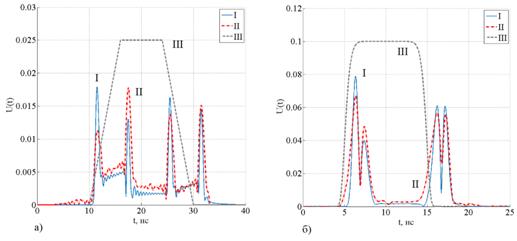
Рис. 3. Огибающая
отраженного сигнала
для падающего импульса c трапецеидальной
огибающей (а) и
с супергауссовой огибающей (б) от трехслойного фильтра
(I –
теория; II – эксперимент; III – огибающая падающего сигнала).
5. Заключение
1. Комплекс проведенных исследований показал наличие более сложного процесса нестационарного отражения в многослойных структурах неотражающего класса с максимально плоской АЧХ по сравнению с однослойными структурами. При малых потерях в слоях структуры огибающая отраженного сигнала может быть приближенно описана Nпроизводной от огибающей падающего сигнала.
2. Было обнаружено, что определяющим фактором, влияющим на характер процесса нестационарного отражения короткого электромагнитного импульса от многослойной структуры, является функциональная зависимость коэффициента отражения многослойной структуры от частоты в окрестности несущей частоты падающего импульса. Заметим, что разные многослойные структуры могут иметь одинаковые коэффициенты отражения в некотором интервале частот. В этом случае короткие электромагнитные импульсы, отраженные от разных структур, будут идентичными с высокой точностью.
3. Установлено, что потери в многослойных интерференционных фильтрах с максимально плоской АЧХ существенно влияют на процесс нестационарного отражения. Теоретически было продемонстрировано, что при отражении амплитудно-модулированного сигнала от фильтров с максимально плоской АЧХ всегда существует момент времени, когда амплитуда отраженного сигнала стремится к нулю.
Литература
1. Бобровников Ю.А., Горохов П.Н., Козарь А.В. Явление нестационарного отражения электромагнитных волн с изменяющейся амплитудой от слоистых структур //Известия Российской академии наук. Серия физическая. – 2002. – Т. 66. – № 12. –С. 1823–1826.
2. Bobrovnikov Y.A., Gorokhov P.N., Kozar' A.V. Transformation of pulses with the help of thin-layer interference structures //Quantum Electronics. – 2003. – V. 33. – № 11. – P. 1019 – 1021.
3. Козарь А.В., Трофимов А.В. Явление нестационарного отражения импульсных сигналов от слоистых структур с потерями //Вестник Московского университета. Серия 3. Физика, астрономия. – 2013. – № 5. – С. 38 – 43.
4. Weiner M.A. Ultrafast optical pulse shaping: A tutorial review //Optics Communications. – 2011. – V. 284. – P. 3669 – 3692.
5. Dunning F.B. Atomic, Molecular, and Optical Physics: Electromagnetic Radiation. London: Academic Press, 1997. – 406 p.
6. Bushuev V.A. Time compression of x-ray free-electron laser pulses under conditions of bragg diffraction //Radioelectronics. Nanosystems. Information Technologies. – 2014. – V. 6. – №. 2. – P. 177 – 186.
7. Macleod H.A. Thin-Film Optical Filters. London: Macmillan, 1986. – 772 p.
8. Фельдштейн А.Л, Явич Л.Р. Синтез четырехполюсников и восьмиполюсников на СВЧ. М.: Связь, 1971. – 352 с.
9. Krepelka J. Maximally flat antireflection coatings //Jemná Mechanika A Optika. – 1992. – V. 37. – P. 53 – 56.
10. Schulz U., Schallenberg U. B., Kaiser N. Symmetrical periods in antireflective coatings for plastic optics //Applied Optics. – 2003. – V. 42. – № 7. – P. 1346 – 1351.
11. Atsuto K., Yasuhiro N., Shinji K. High-precision narrow-band optical filters for global observation. //Proceedings of the International Conference on Space Optical Systems and Applications. – 2012. – P. 12–17.
12. Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973. – 343 с.
13. Proakis J.G., Manolakis D.G. Digital Signal Processing Principles, Algorithms, and Applications (4-th Edition). New Jersey: Prentice Hall, 2006 – 1004 p.
14. Кикоин И.К. Таблица физических величин. М.: Атомиздат, 1976. – 1005 с.
15. Rytting D. Let Time Domain Provide Additional Insight in Network Behavior //Hewlett-Packard RF & Microwave Measurement Symposium and Exhibition. – 1984. – P. 128 – 140.