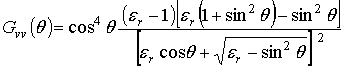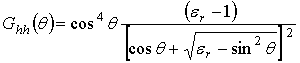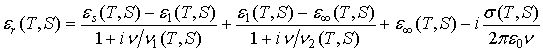Влияние изменчивости физико-химических характеристик морской среды на точность дистанционного определения скорости ветра

УДК 551.46

ВЛИЯНИЕ ИЗМЕНЧИВОСТИ ФИЗИКО-ХИМИЧЕСКИХ ХАРАКТЕРИСТИК МОРСКОЙ СРЕДЫ НА ТОЧНОСТЬ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ СКОРОСТИ ВЕТРА

Ф. В. Кузмин

Севастопольский государственный университет

Статья поступила в редакцию 11 апреля 2016 г.

Аннотация. Анализируются влияние на точность определения скорости приводного ветра изменений температуры и солености приповерхностного слоя океана. Показано, что при изменении температуры проявляются погрешности при дистанционном зондировании морской поверхности в миллиметровом диапазоне длин радиоволн, на больших длинах волн этим эффектом можно пренебречь. Наблюдаемые в натурных условиях типичные изменения солености практически не влияют на точность определения скорости ветра.

Ключевые слова: морская поверхность, дистанционное зондирование, скорость ветра, температура, соленость.

Abstract. The impact of changes in temperature and salinity of the surface layer of the ocean on the accuracy of the definition of near-water wind speed is analyzed. It is shown that errors appear with temperature changes when remote sensing sea surface occurs in millimeter range of radio waves. At longer length of radio waves this effect can be ignored. Typical salinity changes, observed in natural conditions, almost don’t effect on accuracy of the definition of wind speed.

Keywords: sea surface, remote sensing, wind speed, temperature, salinity.

Введение

В настоящее время океанография и метеорология тесно связана с использованием спутниковых методов, средств и технологий. Одним из перспективных направлений спутникового мониторинга является дистанционное определение скорости приводного ветра. Внедрение спутниковых методов в данное направление позволило перейти от эпизодического наблюдения фрагментов процессов на поверхности морей и океанов, к наблюдению и изучению процессов как единого целого в глобальном и региональном масштабах практически в реальном времени [1].

Принцип определения скорости ветра основан на том, что зондирующий радиоимпульс, направленный под углом к морской поверхности, рассеивается из-за её шероховатости, обусловленной короткими ветровыми волнами, энергия которых коррелированна со скоростью ветра [2]. Поэтому уровень рассеянного сигнала зависит от уровня шероховатости морской поверхности [3]. Таким образом, в основе дистанционных измерения скорости приводного ветра лежит связь характеристик коротких поверхностных волн и скорости приводного ветра [4].

Погрешность определения скорости локального ветра, создаваемая неоднозначностью связи уровня шероховатости морской поверхности и скорости воздушного потока над ней, ограничивает предельную точность скаттерометрического и альтиметрического измерения скорости приводного ветра на уровне 1.7 м/с [5, 6]. Изменения температуры и солености влияют на электропроводность и соответственно на уровень рассеянного назад радиосигнала [7, 8]. Влияние изменений температуры и солености на точность определения скорости ветра исследуется в настоящей работе.

2. Радиолокационное определение скорости ветра

Зависимость коэффициента рассеивания радиоволн от скорости ветра различна для разных углов падения, а также для разных направлений падения радиоволн относительно вектора ветра. Эмпирическая модель, описывающая указанные зависимости от скорости ветра и азимутального направления и в определенно степени подтверждаемая теоретическим анализом, имеет вид:

(1)

где pp – вид поляризации, первый индекс соответствует поляризации излучаемого сигнала, второй – принимаемого; u – скорость ветра; – угол по отношению к направлению, противоположному вектору ветра; и – параметры, зависящие от угла падения радиоволн [9].

В табл. 1 представлены констант выражения (1) для различных углов падения .

Таблица 1

Константы регрессионного уравнения (1)

Поляризация

1.85

2.15

2.34

1.76

2.03

2.22

1.95

2.27

2.46

1.62

2.05

2.4

1.54

1.94

2.28

1.7

2.16

2.54

Зависимости от азимутального угла возникает в результате динамического воздействия узконаправленных длинных волн на коротковолновые составляющие волнового поля, которые модулируют их амплитуды [10].

3. Резонансное рассеяние волн морской поверхностью

В случае зондирования морской поверхности в области отсчитываемых от вертикали углов падения θ от 25° до 75° – 80° рассеянный назад сигнал. Рассеяние радиоволн назад создают поверхностные волны, бегущие вдоль направления зондирования в прямом или обратном направлении, волновое число которых связано с волновым числом радиоволн k резонансным соотношением [3].

В нулевом приближении, когда резонансные (брегговские) составляющие поля поверхностных волн распространяются по плоской поверхности, нормированное сечение обратного рассеяния можно представить в форме

, (2)

где – геометрический коэффициент, зависящий от вида поляризации излучаемого и принимаемого радиолокационного сигнала и диэлектрической проницаемости морской воды; – двумерный спектр возвышений морской поверхности, соответствующий волновому вектору брегговской компоненты [11].

При анализе и интерпретации взаимодействия радиоволн с морской поверхностью необходимо учитывать изменения диэлектрической проницаемости морской воды. Эти изменения оказывают влияние на два основных физических механизма, определяющих формирование радиосигнала при однопозиционном зондировании морской поверхности – квазизеркальное отражение и резонансное (брегговское) рассеяние.

Характеристикой, которая определяет зависимость рассеянного назад радиосигнала от физико-химических свойств морской воды, является геометрический коэффициент [12]. Данная зависимость возникает вследствие изменения относительной диэлектрической проницаемости морской воды при изменении ее температуры и солености. Для вертикальной (vv) и горизонтальной (hh) поляризаций функция соответственно имеет вид [3]:

, (3)

. (4)

В свою очередь диалектическая проницаемость морской воды зависит от её температуры и солености. Модель, описывающая данную зависимость, построена на основе двухчастотной аппроксимации Дебая:

, (5)

где T – температура; S – соленость; – частота; – статическая диэлектрическая проницаемость; – промежуточный диэлектрический параметр; – «оптическая» диэлектрическая проницаемость; , – первая и вторая частоты релаксации Дебая; – электропроводность воды; – диэлектрическая постоянная [13].

4. Расчет погрешности определения скорости приводного ветра

Эмпирическая модель [7], описывающая зависимость коэффициента рассеивания радиоволн от скорости ветра (1), была построена на основе большого числа измерений для среднестатистических значений физико-химических параметров морской поверхности. Так как значения параметров морской поверхности (температуры и солености) могут быть различными для каждого конкретного случая, при использовании данной модели возникает погрешность определения скорости ветра. Погрешность является результатом зависимости геометрического коэффициента от диалектической проницаемости морской воды, величина которой, в частности, является функцией температуры и солености [14].

Для определения данной погрешности необходимо определить, в какой мере меняется коэффициент при изменении температуры или солености. Пропорционально этому изменению, как следует из (2), меняется и нормированное сечение обратного рассеяния.

На рис. 1 в качестве примера показаны две зависимости от скорости ветра, рассчитанные согласно (1) и для более высокой температуры. По графику видно, что одному и тому же значению соответствуют два значения скорости ветра. Разность между ними и является ошибкой определения скорости ветра . Для выбранных значений температур она составляет м/с.

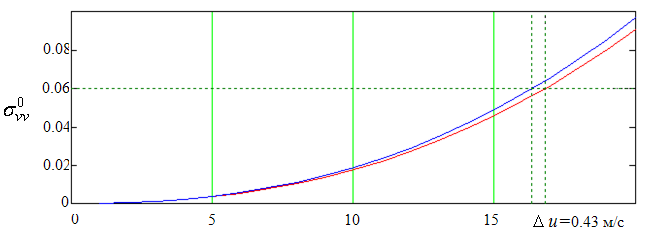
Рис. 1. Зависимости от скорости ветра при разной температуре воды:

18º – красная кривая и 25º – синяя кривая. Расчеты проведены при длине радиоволны, равной 0.4 см.

На рис. 2 представлена зависимость погрешности от скорости приводного ветра при вертикальной поляризации для трех значений угла падения радиоволн , рассчитанные при разности температур 5º.

Из приведенных на рис. 2 графиков видно, что ошибка Δu является мультипликативной, т.е. она пропорциональна скорости ветра. С увеличением длины волны значения Δu быстро убывают, и при зондировании морской поверхности в сантиметровом диапазоне длин волн ими можно пренебречь.

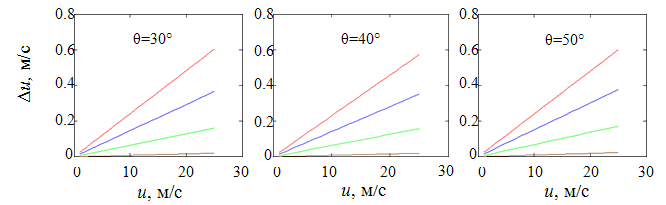
Рис. 2. Зависимости Δu от скорости ветра для вертикальной поляризации радиосигнала, рассчитанные при разности температур 5º.

Длина волны: 0.4 см – красная линия, 0.8 см – синяя линия,

1.5 см – зеленая линия, 3 см – коричневая линия.

Поведение характеристики Δu при зондировании на горизонтальной поляризации в целом подобно ее поведению при зондировании на вертикальной поляризации. Результаты расчетов, выполненные при тех же условиях (углы падения 30°, 40°, 50°, разности температур 5º), для которых рассчитывались значения Δu, представленные на рис. 2., приведены на рис. 3.

Сравнивая представленные на рис. 2 и 3 зависимости Δu от скорости ветра, можно отметить, что влияние разности температур на погрешность определения скорости ветра при зондировании на вертикальной поляризации выше, чем при зондировании на горизонтальной поляризации. В обоих случаях с увеличением длины погрешность, вызванная разностью температур, быстро снижается

На рис. 4 представлена зависимость погрешности определения скорости приводного ветра при вертикальной поляризации для трех значений угла падения радиоволн , рассчитанные при разности солености 5 ‰. Здесь, как и в ситуации, когда погрешность вызвана разностью температур, наблюдается явно выраженная зависимость величины погрешности от длины радиоволны. Из анализа графиков, приведенных на рис. 4 следует, что погрешностью , вызванной изменениями солености можно пренебречь.

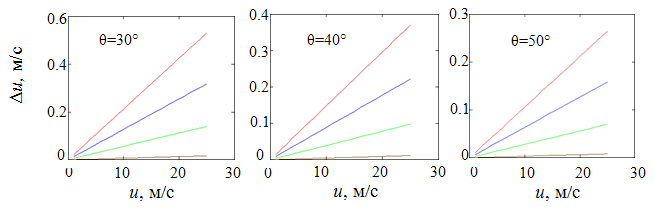
Рис. 3. Зависимости Δu от скорости ветра для горизонтальной поляризации радиосигнала, рассчитанные при разности температур 5º.

Длина волны: 0.4 см – красная линия, 0.8 см – синяя линия,

1.5 см – зеленая линия, 3 см – коричневая линия.

5. Обсуждение результатов

Оценка точности спутниковых измерений скорости ветра осуществляется путем сопоставления данных радиолокационных измерений и прямых измерений ветра, выполненных с океанографических буев, которые установлены в океане. При этом погрешность регрессионных уравнений, связывающих скорость ветра и уровень рассеянного назад радиосигнала, определяется несколькими факторами. К таким факторам относятся: неоднозначностью связи уровня шероховатости морской поверхности и скорости ветра [5], изменения характеристик длинных волн [16], которые косвенно влияют на резонансное рассеяние радиоволн, воздействуя на короткие (резонансные) волны [10], изменениями физико-химических характеристик морской воды [8]. Существуют также ошибки калибровки, вызванные несинхронностью измерений со спутника и с буя, а также отклонением трассы спутника от местоположения буя [17]. Очевидно, что каждая из указанных ошибок должна быть меньше суммарной.

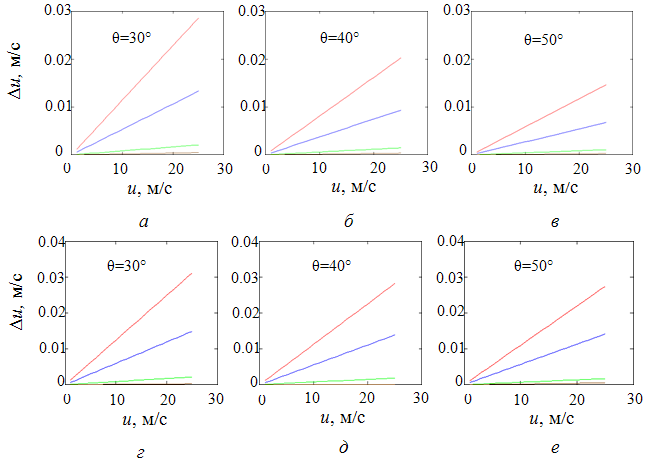
Рис. 4. Зависимость Δu от скорости ветра для вертикальной (а, б, в) и горизонтальной (г, д, е) поляризации радиосигнала, рассчитанные при разности солености 5 ‰. Длина волны: 0.4 см – красная линия, 0.8 см – синяя линия, 1.5 см – зеленая линия, 3 см – коричневая линия.

В настоящее время точность определения скорости приводного ветра составляет примерно 1.7 м/с [18]. Уже в первых экспериментах были получены данные о скорости ветра с точностью, близкой к указанной. То, что с развитием технических средств и методов калибровки радиолокаторов для измерений ветра точность не улучшается, указывает на то, что существуют физические механизмы ее ограничивающие. Одним из таких механизмов является изменение электропроводности морской воды под границей раздела воздух-вода.

Полученные в данной работе величины погрешности при изменении температуры указывают на возможность повышения точности определения скорости ветра по данным радиолокационных измерений при зондировании в миллиметровом диапазоне. Для этого необходимо использовать дополнительную информацию о поле поверхностной температуры. Изменения солености, при зондировании как в миллиметровом, так и в сантиметровом диапазонах, на точность измерения скорости ветра не влияют.

Выводы

Проведен анализ влияния на точность скаттерометрического определения скорости приводного ветра изменений температуры и солености приповерхностного слоя океана. Показано, что изменения температуры сильнее проявляются на вертикальной поляризации, чем на горизонтальной. С увеличением длины зондирующей радиоволны эффект быстро уменьшается. Для радиоволн сантиметрового диапазона и более длинных волн влиянием изменений температуры в пределах 5º можно пренебречь.

Погрешность, создаваемая изменениями солености мала, и ей можно пренебречь при зондировании морской поверхности во всех диапазонах радиоволн.

Литература

1. Пустовойтенко В.В., Запевалов А.С. Оперативная океанография: Спутниковая альтиметрия – Современное состояние, перспективы и проблемы // Серия. Современные проблемы океанологии, Севастополь: НПЦ “ЭКОСИ-Гидрофизика”. 2012. Вып. № 11. 218 с.

2. Moore R. K., Pierson W.J. Measuring sea state and estimating surface winds from a polar orbiting satellite // Proc. Inter. Symp. Electromagnetic Sensing of the Earth from Satellites Miami Beach, FL. - 1966. - Nov. 22-24. - P. R1-R28.

3. Valenzuela G. Theories for the interaction of electromagnetic and ocean waves.- A Review // Boundary Layer Meteorology. 1978. Vol. 13, № 1-4. P. 61-85.

4. Христофоров Г.Н., Запевалов А.С., Смолов В.Е Зависимость амплитудных характеристик высокочастотных компонент спектра ветровых волн от скорости ветра над морем // Морской гидрофизический журнал. 1993. № 3. С. 67-77.

5. Христофоров Г.Н., Запевалов А.С., Смолов В.Е. О предельной точности скаттерометрического определения со спутника скорости ветра над океаном // Исследование Земли из космоса, 1987, № 2, С. 57-65.

6. Запевалов А.С., Показеев К.В., Пустовойтенко В.В. О предельной точности альтиметрического определения скорости приводного ветра // Исследование Земли из космоса, 2006, № 3, С. 49-54.

7. Терехин Ю.В., Пустовойтенко В.В. Влияние температуры и солености морской воды на характеристики радиолокационного сигнала СВЧ-диапазона // Исследование Земли из космоса. 1986. № 2. С. 16-20.

8. Садовский И.Н., Кузьмин А.В., Шарков Е.А., Сазонов Д.С., Пашинов Е.В., Ашеко А.А., Батулин С.А. Анализ моделей диэлектрической проницаемости водной среды, используемых в задачах дистанционного зондирования акваторий // Препринт. М.: ИКИ РАН, 2002, Пр-2172. 60 с.

9. Мур Р., Фэн А. К. Радиолокационное определение параметров ветра над морем // ТИИЭР. 1979. Т. 67. С. 40-63.

10. Запевалов А.С. Моделирование брегговского рассеяния электромагнитного излучения сантиметрового диапазона морской поверхностью. Влияние волн более длинных, чем брегговские составляющие // Известия РАН. Физика атмосферы и океана. 2009. Т. 45, № 2. С. 266-275.

11. Kudryavtsev V.N., Hauser D., Caudal G., Chapron B.A. A semi-empirical model of the normalized radar cross-section of the sea surface. 1 Background model // J. Geophys. Res. 2002. Vol. 107, № 0, XXXX, doi:10.1029/2001JC001003.

12. Запевалов А.С., Пустовойтенко В.В. Влияние физико-химических характеристик морской воды на резонансное рассеяние радиоволн морской поверхностью // Журнал Радиоэлектроники [электронный журнал]. 2014. № 9. URL: http://jre.cplire.ru/iso/sep14/4/text.pdf

13. Meissner T., Wentz F.J. The complex dielectric constant of pure and sea water from microwave satellite observations // IEEE Transactions on Geoscience and Remote Sensing, 2004. Vol. 42, No. 9. P. 1836-1849.

14. Guillou C., Ellison W., Eymard L., Lamkaouchi K., Prigent C., Delbos G., Balana G., Boukabara S.A. Impact of new permittivity measurements on sea surface emissivity modeling in microwaves // Radio Sci. 1998. Vol. 33. P. 649-667.

15. Запевалов А.С. Наблюдения шероховатости морской поверхности в период апвеллинга // Морской гидрофизический журнал. 2001. №2. С. 36-43.

16. Запевалов А.С., Большаков А.Н., Смолов В.Е. Моделирование плотности вероятностей возвышений морской поверхности с помощью рядов Грама-Шарлье // Океанология. 2011. Т. 51, № 3. С. 432–439.

17. Gommenginger C.P., Srokosz M.A., Challenor P.G., Cotton P.D. Development and validation of altimeter wind speed algorithms using an extended collocated buoy/topex dataset // IEEE Transactions on Geoscience and Remote Sensing. 2002. Vol. 40, No. 2. P. 251-260.

18. Караев В.Ю., Каневский М.Б., Баландина Г.Н., Коттон Д. Трехпараметрический алгоритм определения скорости приповерхностного ветра по данным радиоальтиметрических измерений // Исследование Земли из космоса. 1999. № 6. С. 33-41.