Обнаружение ошибок кодом на основе преобразования Крестенсона над полем GF(4)

УДК 621.391

Обнаружение ошибок кодом на основе преобразования Крестенсона над полем GF(4)

В. А. Вершинин

Рыбинский государственный авиационный технический университет

им. П. А. Соловьева

Статья поступила в редакцию 16 июня 2016 г.

Аннотация. В статье рассматривается спектральное кодирование на основе преобразования Крестенсона над полем GF(4). Цель кодирования – обнаружение ошибок. Произведена оценка эффективности кодирования, когда число ошибок в кодовом слове больше числа гарантированно обнаруживаемых ошибок.

Ключевые слова: спектральное кодирование, обнаружение ошибок, преобразование Крестенсона.

Abstract. The article discusses the spectral encoding based conversion of Christenson over the field GF(4). The purpose of the encoding is error detection. The effectiveness of encoding is evaluated in the case when the number of errors in code word larger than the number of guaranteed detectable errors. Simulation of the decoding process showed that the highest value of the probability of undetected error is obtained when the number of errors in the code word equal to the code distance. This probability is used in the article to estimate from above the probability of undetected error. If the number of errors in the code word is greater than or equal to the code distance, the increase of the length of the code words under the condition of constant value of the code distance gives the opportunity to obtain an acceptable value of probability of undetected error.

Key words: spectral encoding, error detection, transformation of Christenson.

1. Введение

Рассмотрим спектральное кодирование на основе преобразования Крестенсона над полем GF(4) [1]. Элементы поля обозначим 0, 1, 2, 3. Сложение и умножение над полем GF(4) определим следующим образом:

+	0	1	2	3	·	1	2	3
0	0	1	2	3	0	0	0	0
1	1	0	3	2	1	1	2	3
2	2	3	0	1	2	2	3	1
3	3	2	1	0	3	3	1	2

Ядро преобразования над полем GF(4) представляется в виде матрицы:

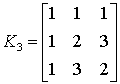Преобразование порядка , где определяется как тензорная степень ядра: . Обратное преобразование задается матрицей обратной по отношению к . Например,

, .

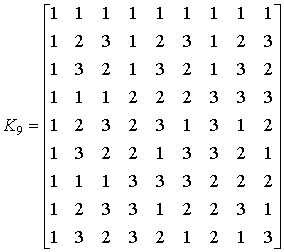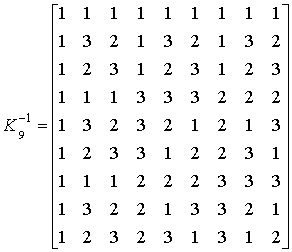В составе матрицы Крестенсона [2] (как прямой, так и обратной) имеется m особых строк (столбцов) с номерами , поэлементным произведением которых можно получить любую другую строку (столбец). Для получения строки с заданным номером (за исключением нулевой) необходимо в качестве сомножителей взять особые строки, сумма номеров которых равна заданному (каждая особая строка входит в произведение не более двух раз). Здесь и далее предполагается, что нумерация элементов начинается с нуля. Условимся для удобства последующего изложения называть элементы некоторого вектора с номерами особых строк элементами типа 1, элементы с номерами, получающимися сложением номеров двух особых строк, – элементами типа 2, элементы с номерами, которые можно получить сложением номеров трёх особых строк, – элементами типа 3 и так далее. Элемент с нулевым номером будем считать элементом типа 0.

2. Кодирование

Пусть блоку элементов сообщения длиной k соответствует вектор , элементы которого могут принимать значения 0, 1, 2, 3. Образуем вектор , k элементов которого равны элементам вектора a и называются информационными, а остальные являются нулевыми и называются проверочными. Какие элементы являются проверочными, определяется параметром s, который называется порядком кода и может принимать значения . В кодах на основе преобразования Крестенсона

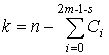где – количество элементов типа i.

В качестве проверочных в векторе b для выбирается нулевой элемент, для выбирается нулевой элемент и элементы типа 1, для к указанным выше проверочным элементам добавляются элементы типа 2 и т.д.

Поставим в соответствие кодовому слову длиной n кодовый вектор . Формирование этого вектора осуществляется с помощью обратного преобразования Крестенсона:

. (1)

Код, определенный таким образом имеет кодовое расстояние

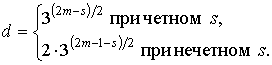
В таблице 1 приведены основные характеристики рассматриваемых кодов при определенных значениях n.

Таблица 1

n	k при
n	d=2	d=3	d=6	d=9	d=18	d=27	d=54	d=81	d=162	d=243
27	26	23	17	10	4	1	-	-	-	-
81	80	76	66	53	28	15	5	1	-	-
243	242	237	222	192	147	96	51	21	6	1

3. Декодирование с обнаружением ошибок

Пусть кодовому слову на входе декодера соответствует вектор

, (2)

где e – вектор ошибок. Этот вектор связан с наличием помех в канале связи. Если в результате действия помех искажаются элементы кодового слова, то соответствующие элементы вектора ошибок принимают значение 1, 2 или 3. Неискаженным элементам кодового слова соответствуют нулевые элементы вектора ошибок. В декодере осуществляется прямое преобразование Крестенсона вектора c', в результате получается вектор . Учитывая (1) и (2),

. (3)

Очевидно, что при отсутствии ошибок и . Обнаружение ошибок в кодовом слове осуществляется путем контроля значений проверочных элементов вектора b'. Если хотя бы один из проверочных элементов не равен нулю, то это соответствует обнаружению ошибок. Гарантировано обнаруживаются ошибки, если их количество в кодовом слове не превышает . Если число ошибок больше , то ошибки могут быть не обнаружены с определенной вероятностью. Оценка этой вероятности является целью данной статьи.

4. Вероятность необнаруженной ошибки

Будем оценивать вероятность необнаруженной ошибки при фиксированном числе r ненулевых элементов вектора ошибок. При этом предполагаем, что все возможные варианты размещения ненулевых элементов равновероятны и каждый из этих элементов с равной вероятностью принимает значение 1, 2, 3. Очевидно, что вероятность необнаруженной ошибки равна нулю при .

Моделирование процесса декодирования показало, что наибольшее значение вероятности необнаруженной ошибки получается при . Именно эту вероятность P будем использовать для оценки сверху вероятности необнаруженной ошибки при фиксированном значении r.

Образуем матрицу g, состоящую из столбцов матрицы с номерами проверочных элементов. Таким образом, матрица g имеет n строк и столбцов. Любые строки матрицы g, соответствующие ненулевым элементам вектора e, являются линейно независимыми. Тогда при произведение и такие ошибки всегда обнаруживаются. При , для определенных размещений ненулевых элементов вектора e и определенных значений этих элементов возможно , что соответствует необнаруженным ошибкам.

Пусть u – число линейно независимых строк матрицы g, соответствующих ненулевым элементам вектора e, значение u может быть , либо d. Очевидно, что вероятность размещения , при котором возможно равна вероятности значения . Вероятность ненулевых значений элементов вектора e при условии , для которых равна . Выражение для получено из следующих соображений. Число возможных комбинаций ненулевых значений элементов вектора e равно , из них 3 (при условии ) приводят к . Тогда

. (4)

Вероятность определяется путем проведения N испытаний при различных размещениях d ненулевых элементов в векторе ошибок с использованием пакета Matlab. При каждом испытании определяется ранг матрицы, которая получается из матрицы g путем исключения из нее строк, соответствующих нулевым элементам вектора e. При этом определяется число испытаний с рангом, равным . Число всех возможных размещений d ненулевых элементов в векторе ошибок размерностью n равно . Здесь – биномиальный коэффициент. При проведении испытаний для всех возможных размещений () получается точное значение . При случайно формируемых размещениях с помощью функции binofit(N1,N) пакета Matlab получаем точечную оценку значения, нижнюю и верхнюю границу оценки с доверительной вероятностью 0.95.

Далее на основании (4) можно определить P, , , , причем при определении точечной оценки значения P, нижней и верхней границы оценки в (4) вместо используется , и соответственно.

Результаты, полученные указанным путем, для кодов (27,17), (81,66), (243,222) на основе преобразования Крестенсона помещены в таблице 2. Все эти коды имеют .

Таблица 2

Код (n,k)	(27,17)	(81,66)	(243,222)
Характер испытаний	Все возможные размещения,	Случайные размещения,	Случайные размещения,
	198	195	6
		^–	–
	–
,	–	,	,
P		–	–
	–
,	–	,	,

5. Выводы

Если число ошибок в кодовом слове больше , то с ростом длины кодового слова n и постоянном значении d вероятность необнаруженной ошибки уменьшается и при достаточно большом n можно получить приемлемое значение этой вероятности.

С увеличением n при постоянном значении d увеличивается скорость кода , что также является положительным фактом.

Литература

1. Муттер В.М. Основы помехоустойчивой телепередачи информации.– Л.: Энергоатомиздат, 1990.– 288 с.

2. Передача дискретных сообщений/ Вершинин В.А. Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева. Рыбинск, 2002.– 82 с.– Деп. в ВИНИТИ 17.12.2002 г., № 2196-В2002.