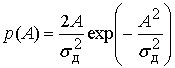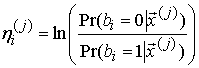УДК 621.391.01

ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ НЕКОГЕРЕНТНОГО ПРИЕМА ПОСЛЕДОВАТЕЛЬНЫХ ТУРБО-КОДОВ НА ОСНОВЕ СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ ПРИ ПЕРЕДАЧЕ ПО НЕСТАЦИОНАРНЫМ КАНАЛАМ

 

Л. Е. Назаров ¹, П. В. Шишкин ²

¹ Институт радиотехники и электроники им. В.А.Котельникова РАН, Фрязинский филиал, г. Фрязино

² АО «Информационные спутниковые системы» им. академика  М.Ф.Решетнева,
г. Железногорск

 

Статья поступила в редакцию 24 мая 2016 г.

 

Аннотация. Приведено описание сигнальных конструкций на основе последовательного турбо-кода с использованием сигналов с относительной фазовой манипуляцией. Эти сигнальные конструкции перспективны для использования в системах передачи информации по нестационарным каналам с межсимвольным программным переключением частот. Даны описания алгоритмов некогерентного приема этих сигнальных конструкций и результаты моделирования с целью оценки вероятностных характеристик при их приеме.

Ключевые слова: турбо-коды, сигналы, относительная фазовая манипуляция, каналы передачи, некогерентный прием, вероятностные характеристики, нестационарность.

Abstract. The description of signal constructions based on sequential turbo-code and differential phase keying is described in the article. These signal constructions are perspective for using in communication systems under non-stationary channels and with frequency hopping. The non-coherent iterative decoding algorithms for these signals and error-performances of that are presented in the article.

Key words: turbo-codes, signals, differential phase-keying, channel, non-coherent decoding, error-performance, non-stationary channels.

 

 

Введение

Выбор эффективных сигнальных конструкций в сочетании с помехоустойчивым кодированием и методов их обработки при приеме определяются характеристиками физических каналов передачи [1].

При анализе вероятностных характеристик систем связи различного назначения базовая модель для каналов передачи основана на использовании стационарного аддитивного белого гауссовского шума (АБГШ) [2]. Реальные каналы передачи для широкого ряда систем связи (например, для спутниковых и наземных подвижных систем связи) имеют ряд отличительных свойств по отношению к АБГШ, учёт которых необходим при организации надёжной передачи информации [1,2]. Важными факторами снижения надёжности передачи для данных систем связи являются нестационарность каналов, обусловленная многолучевостью распространения сигналов в мобильных системах связи [3] (наземная подвижная система связи сотового формата GSM [3], спутниковые подвижные системы связи), а также изменение характеристик физической среды распространения сигналов (например, изменение электрических свойств ионосферных линий передачи спутниковых систем связи, ионосферных линий передачи систем связи коротковолнового диапазона, тропосферных линий передачи систем дальней тропосферной связи [4]).

Результаты экспериментальных и модельных исследований в части оценивания времени стационарности для ряда каналов  приведены в ряде работ, например в [3-7]. Для каналов дальней тропосферной связи значение  достигает 200 мсек [5]. Для линий ионосферных систем связи коротковолнового диапазона средней дальности в обычных условиях значения  не превышают 100…150 мсек [6]. Время стационарности ионосферных каналов передачи спутниковых систем связи зависит от частотного диапазона, времени суток (день, ночь), географического размещения приемных станций: для Р-частотного диапазона и низких широт () оценочные значения  с, для средних широт () оценочные значения  с, для высоких широт  оценочные значения  с [7].

Многолучевость и влияние среды распространения определяют наличие межсимвольной и межканальной интерференции в цифровых системах связи и, как следствие, в дополнение к АБГШ возникновение мультипликативных помех. Для снижения влияния этого типа помех разработан ряд методов, основанных на использовании эффективных сигнальных конструкций и на применении соответствующей обработки при их приёме. Например, в современных цифровых системах связи (IEEE802.11(WiFi), IEEE802.16(WiMax), DVB-SH (цифровое спутниковое телевещание), 3GPP LTE (мобильная связь 4G)) используются широкополосные сигналы с ортогональным частотным мультиплексированием OFDM (orthogonal frequency-division multiplexing) [3]. В подвижной системе связи сотового формата GSM осуществляется периодическое оценивание изменяющейся во времени импульсной характеристики линии передачи и с её использованием выполняется обработка сигналов при приёме, реализующая правило максимального правдоподобия [3].

Эффективный метод организации надежной передачи информации по рассматриваемым нестационарным каналам основан на переключении рабочих частот (ПРЧ). При этом сигнальные конструкции представляются в виде последовательности парциальных сигналов, передаваемых на различных частотных позициях. Время передачи парциальных сигналов сравнимо со временем стационарности канала. В этом случае возможна когерентная обработка парциальных сигналов, однако при приеме нужно учитывать априорную неопределенность относительно начальных фаз парциальных сигналов в составе сигнальной конструкции. Это определяет необходимость оценивания этих фаз, например, с использованием пилот-сигналов [3], либо применять сигнальные конструкции, прием которых осуществляется без оценки начальных фаз (некогерентный приём) [1, 8].

В работе развивается направление ПРЧ с использованием сигнальных конструкций с некогерентным приёмом парциальных сигналов. Рассматриваемые сигнальные конструкции основаны на использовании сигналов с относительной фазовой модуляцией (ОФМ) [1] в сочетании с последовательными турбо-кодами [9,10].

1. Постановка задачи

Рассматривается система связи, реализующая метод ПРЧ: длительность парциальных сигналов на частотной позиции равна , информационная скорость  (бит/с), длительность информационных символов . В канале присутствует АБГШ с односторонней спектральной плотностью . Полагается выполнение тактовой синхронизации сигналов на входе сигнального демодулятора и выполнение кадровой синхронизации.

Для нестационарных многолучевых каналов начальные фазы  парциальных сигналов при использовании метода ПРЧ полагаются случайными величинами с равномерным законом распределения . При наличии сигнала прямой видимости с амплитудой  плотность распределения  огибающей  общего сигнала с учетом многолучевых компонент с мощностью  на входе приемной антенны может задаваться законом Релея-Райса, характеризуемое коэффициентом Райса 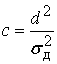 [1,3]

 

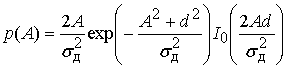.                                    (1)

Здесь  - модифицированная функция Бесселя первого рода 0-го порядка.

При отсутствии сигнала прямой видимости плотность распределения  огибающей  входного сигнала определяется законом Релея [1]

.                                                          (2)

В зависимости от отношений между  и  методы ПРЧ классифицируются на внутрисимвольные и межсимвольные [11].

Для метода внутрисимвольного ПРЧ выполняется условие , когда лишь часть информационного бита передается на времени частотной позиции. Реализация этого метода с использованием сигнальных конструкций на основе последовательных турбо-кодов с каскадированием совокупности кодов-повторений приведена в [12]. В качестве парциальных сигналов использовались ортогональные сигналы Уолша. Для этих сигнальных конструкций разработаны алгоритмы некогерентного приема.

Ниже рассматривается метод межсимвольной ПРЧ, при котором выполняется условие  и несколько информационных битов передается на частотной позиции. В работах [13-16] приведены результаты по развитию этого направления, исследуемые сигнальные конструкции формируются на основе блоковых турбо-кодов с высокой кодовой скоростью в сочетании с парциальными ортогональными сигналами Уолша. Для этих сигнальных конструкций также разработаны алгоритмы некогерентного приема.

Суть задачи - привести описание сигнальных конструкций и алгоритмов их некогерентного итеративного приема на основе помехоустойчивых последовательных турбо-кодов с низкой кодовой скоростью в сочетании с сигналами ОФМ, перспективных для реализации направления межсимвольной ПРЧ для нестационарных каналов передачи.

2. Описание последовательных турбо-кодов на основе сигналов ОФМ для ПРЧ

Рассматриваемая помехоустойчивая кодовая конструкция входит в класс последовательных турбо-кодов с пониженной сложностью алгоритмов приема [9,10]. Общая блок-схема формирования этих кодов приведена на рис.1, она содержит внешний помехоустойчивый код , перемежитель  и внутренний помехоустойчивый код .

 

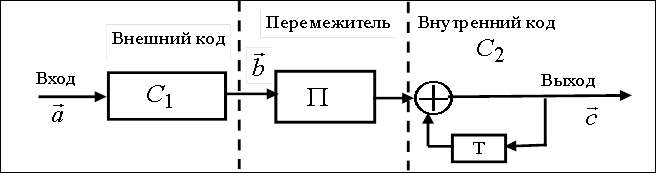
Рис.1. Общая блок-схема формирования помехоустойчивые последовательных турбо-кодов
( - регистр задержки на такт,  - сложение по mod2).

 

Результаты исследований свойств и вероятностных характеристик этих кодов приведены в ряде работ, например в [12,17,18]. В работе [18] в качестве внешнего кода  рассмотрен нерекурсивный сверточный код с кодовой скоростью 1/2 и с числом состояний в кодовой решетки, равным 4. В работе [17] в качестве кода  использована совокупность кодов с обобщенной проверкой на четность. В работе [12] исследовались вероятностные характеристики рассматриваемой кодовой конструкции с использованием кодов повторений. Для данных кодов разработаны эффективные алгоритмы итеративного приема, реализующие правило посимвольного приема. Путем теоретического анализа и компьютерного моделирования работы этих алгоритмов показано достижение практически предельных вероятностных характеристик при приеме рассматриваемых кодов, определяемых пропускной способностью каналов передачи АБГШ.

В настоящей работе в качестве внешнего кода  используется совокупность  блоковых систематических кодов с параметрами () на основе ортогональных базисных функций Уолша-Адамара [1,19]. Здесь  - длительность кодовых слов кода ;  - размерность базиса функций Уолша-Адамара. Внутренний код  является рекурсивным сверточным кодом с минимальным возможным числом состояний в кодовой решетке  и . Начальное состояние кодера . Фрагмент кодовой решетки данного кода приведен на рис.2.

 

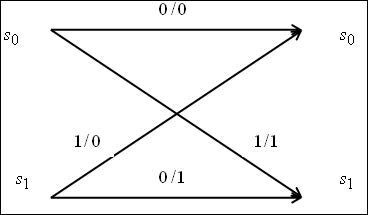
Рис.2. Фрагмент решетчатой структуры рекурсивного сверточного кода  с двумя состояниями
(обозначение  соответствует проверочному символу  для информационного символа ).

Кодирование осуществляется следующим образом - входная информационная последовательность  длительностью  разбивается на  групп одинаковой длительности , каждая из которых поступает на вход соответствующего кодера кода () в составе . Для последовательности  длительность кодовых слов  на выходе кодера  равна . Последовательность символов  с выхода кода  поступает на устройство перемежения П и далее на вход кодера внутреннего кода .

Модификация внутреннего кода  для согласования с ПРЧ заключается в формировании 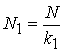 подпоследовательностей ,  для каждой последовательности  из  символов с выхода перемежителя . При этом кодовые решетки подпоследовательностей  начинаются и заканчиваются состоянием , что определяется включением дополнительного символа  для каждой последовательности  по правилу: , если после обработки  состояние кодера  и  в противном случае. 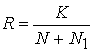Длительность кодовых слов кода равна , кодовая скорость , на частотных позициях находится  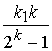информационных битов. Результирующая последовательность кодовых символов  с выхода  является манипуляционной при формировании сигналов ОФМ.

 

3. Алгоритм некогерентного приема последовательных турбо-кодов

Пусть на частотной позиции передается сигнал ОФМ, соответствующий  последовательности ;  и  - прямая и квадратурная реализации с выхода демодулятора с отчетами [1]

,                                            (3)

.                                            (4)

Здесь  - амплитуда сигналов;  - помеховые составляющие, статистически независимые, с гауссовским законом распределения с нулевыми средними и с дисперсиями ;  - длительность символов сигналов ОФМ.

 

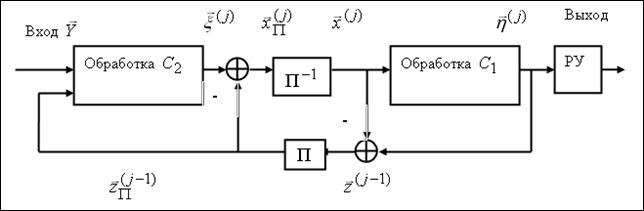
Рис.3. Блок-схема алгоритма итеративного приема последовательного турбо-кода (РУ - решающее устройство).

 

На рис.3 приведена блок-схема алгоритма итеративного приема рассматриваемой кодовой конструкции, которая является общей для последовательных турбо-кодов [10,20]. Итерация итеративного приема включает два этапа.

На первом этапе -ой итерации в блоке “обработка ” вычисляются отношения апостериорных вероятностей для символов внутреннего кода

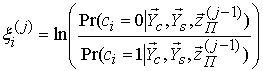.                                           (5)

и далее вычисляется функционал . Здесь  - апостериорные вероятности символов кода ;  - вектор априорной информация символов кода  на  итерации, на первой итерации его отсчеты полагаются равными 0.

На втором этапе -ой итерации алгоритма итеративного приема в блоке “обработка ” вычисляются отношения апостериорных вероятностей  для символов внешнего кода

                                                         (6)

и далее вычисляется функционал , где  - отсчеты деперемеженной последовательности . Последовательность  с выхода блока перемежения  отсчетов  принимается в качестве априорной информации  для последующей -ой итерации.

После реализации задаваемого числа итераций решающим устройством вычисляются оценки информационных символов : если , то  и  в противном случае.

Приведем описания процедур вычисления отношений символьных апостериорных вероятностей  для составляющих кодов , .

4. Алгоритмы вычисления символьных апостериорных вероятностей для составляющего сверточного кода

При вычислении на первом этапе отношений вероятностей  (5) используется алгоритм MAP (maximum a’posteriori probability), реализующий правило посимвольного приема и основанный на представлении сверточного кода в виде решетчатой структуры [9].

Суть алгоритма MAP - вычисление двух рекуррентных соотношений, которые для рассматриваемого сверточного кода имеют вид [9]

, , ,            (7)

,                                                     (8)

, , ,     (9)

.                                                     (10)

Здесь  - длительность подпоследовательностей  с дополнительным символом ; ; - состояния кодовой решетки (рис.2);  - метрика перехода между состояниями решетки  ( и ), задаваемая соотношением

.    (11)

Если между состояниями  и  решетки существует переход, то в (11) , в противном случае .

Вероятности  в (11) задаются соотношениями 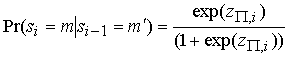, если  и 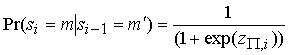, если . Здесь  - символьная априорная информация, вычисляемая для каждой итерации.

Для АБГШ канала справедливо выражение относительно множителя в (11) , здесь  - постоянная.

Результирующее выражение для отношения апостериорных символьных вероятностей  имеет вид

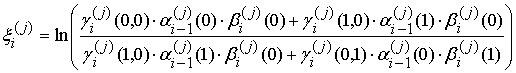.                 (12)

При реализации процедуры MAP требуется оценка параметра , необходимо также вычисление нелинейных функций , , что усложняет ее реализацию. Модификация данной процедуры log_max_МАР является более простой относительно реализации, так как не требует оценки энергетического параметра и требуются лишь операции “сложение-вычитание-сравнение”. Соответствующие выражения имеют вид [9]

, , ,     (13)

,                                               (14)

, , , (15)

.                                        (16)

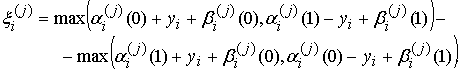                            (17)

Процедура log_max_МАР, используемая для согласования с ПРЧ, заключается в вычислении значений ,  для последовательностей , соответствующих парциальным подпоследовательностям , . Отсчеты последовательностей  при вычислении (13)-(17) для  задаются в виде

.                                                            (18)

Таким образом, вычисление совокупности последовательностей  выполняется для значений начальных фаз . Здесь  - множество используемых дискретных начальных фаз. Выбор соответствующего значения  и последовательностей ,  при вычислении величин  (15) для второго этапа итерации определяется условием выбора максимума

.                                                                         (19)

 

5. Алгоритм вычисления символьных апостериорных вероятностей для составляющих блоковых кодов в составе

Вычисление отношений апостериорных вероятностей  (6) для символов внешнего кода  основано на использовании соотношения [9]

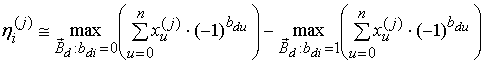.                     (20)

При вычислении (20) применяется модифицированный алгоритм быстрого спектрального преобразования в базисе Уолша-Адамара размерностью  с операциями “сравнение-пересылки” [9].

 

6. Результаты вычислений

На рисунке 4 приведены вероятности ошибки на бит  для рассматриваемого метода ПРЧ в зависимости от количества используемых дискретных начальных фаз  (кривая 1),  (кривая 2),  (кривая 3). По оси абсцисс отложены значения сигнал/помеха ,  - энергия сигналов на информационный бит. В качестве внешнего кода  сигнальной конструкции используется совокупность  блоковых систематических кодов с параметрами (15,4), на частотных позициях располагаются 20 информационных битов. Информационный объем сигнальной конструкции равен 1024 битов, кодовая скорость . Моделирование алгоритма некогерентного приема сигнальной конструкции (20 итераций) произведено для АБГШ канала, что соответствует наличию сигнала прямой видимости и выполнению условия для коэффициента Райса . Видно, что вероятностные кривые 1 () и 2 () практически совпадают, различия энергетических параметров для одинаковых значений  не превышают 0.05 дБ. Вместе с тем, различия значений сигнал/помеха для вероятностных кривых 1 () и 3 () достигают 0.2 дБ.

 

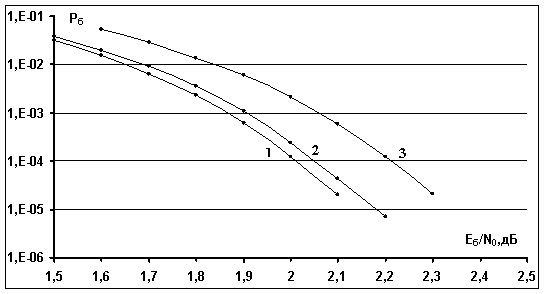
Рис.4. Вероятностные кривые некогерентного приема сигнальной конструкции с использованием в качестве внешнего кода совокупности  блоковых кодов (15,4) в зависимости от количества используемых дискретных начальных фаз  (кривая 1),  (кривая 2),  (кривая 3) (20 итераций, информационный объем 1024 битов, на частотных позициях ≈20 битов, АБГШ канал).

 

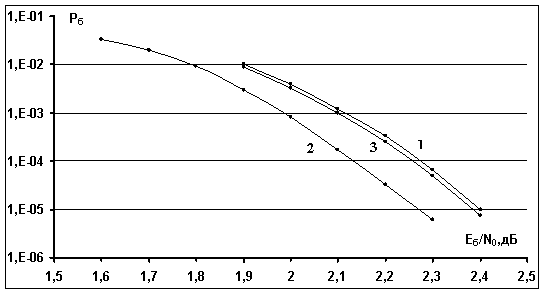
Рис. 5. Вероятностные кривые некогерентного приема сигнальных конструкций (20 итераций, АБГШ канал): 1 - использование в качестве внешнего кода совокупности  блоковых кодов с параметрами (31,5); 2 - использованию в качестве внешнего кода совокупности  блоковых кодов с параметрами (15,4); 3 - использование в качестве внешнего кода сверточного нерекурсивного кода с кодовой скоростью 1/2.

На рисунке 5 приведены вероятности ошибки  для рассматриваемых сигнальных конструкций (кривые 1, 2). Кривая 1 соответствует использованию в качестве внешнего кода при формировании сигнальной конструкции совокупности  блоковых кодов с параметрами (31,5) (на частотных позициях ≈15.5 битов, кодовая скорость ), кривая 2 соответствует использованию в качестве внешнего кода совокупности  блоковых кодов с параметрами (15,4) (на частотных позициях 20 битов). В качестве сравнения приведена также кривая 3, соответствующая использованию описанного в работе [18] последовательному турбо-коду на основе внешнего кода  в виде сверточного нерекурсивного кода с кодовой скоростью 1/2 и с числом состояний в кодовой решетке, равным 4 (на частотных позициях 19 битов, кодовая скорость ). Информационный объем рассматриваемых сигнальных конструкций ≈1000 битов. Моделирование алгоритмов некогерентного приема рассматриваемых сигнальных конструкций при получении вероятностных кривых на рисунке 5 произведено для АБГШ канала и для множества дискретных начальных фаз объемом . Видно, что вероятностные кривые 1 и 3 практически совпадают - различия энергетических параметров для одинаковых значений  в рассматриваемом диапазоне вероятностей ошибок приема не превышают 0.025 дБ. Видно также, что сигнальная конструкция с использованием совокупности блоковых кодов с параметрами (15,4) характеризуется большей помехоустойчивостью - энергетический выигрыш соответствующей кривой 2 для  по отношению к кривым 1 и 3 превышает 0.1 дБ.

 

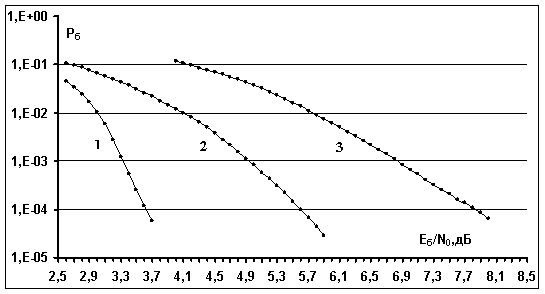
Рис. 6. Вероятностные кривые некогерентного приема сигнальных конструкций (20 итераций, Релеевское распределение амплитуды сигналов при наличии АБГШ): 1 - использование в качестве внешнего кода совокупности  блоковых кодов с параметрами (31,5); 2 - использованию в качестве внешнего кода совокупности  блоковых кодов с параметрами (15,4); 3 - использование в качестве внешнего кода сверточного нерекурсивного кода с кодовой скоростью 1/2.

На рисунке 6 приведены вероятности ошибки  для рассматриваемых сигнальных конструкций, вероятностные характеристики некогерентного приема которых приведены на рисунке 5. Моделирование алгоритмов некогерентного приема этих сигнальных конструкций при получении вероятностных кривых произведено для многолучевого канала при отсутствии сигнала прямой видимости с плотностью распределения  амплитуды  сигнала, определяемой законом Релея (2), при наличии АБГШ и для множества дискретных начальных фаз объемом . В этом случае энергетический параметр  эквивалентен средней энергии сигналов на информационный бит. Видно, что сигнальная конструкция с использованием сверточного нерекурсивного кода с кодовой скоростью 1/2 в качестве внешнего кода [18] характеризуется наименьшей помехоустойчивостью - вероятность ошибки  достигается при 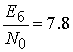 дБ. При уменьшении кодовой скорости рассматриваемых сигнальных конструкций помехоустойчивость некогерентного приема увеличивается - вероятность ошибки  достигается при 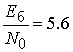  дБ и при 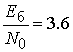 дБ для сигнальных конструкций с кодовой скоростью  (кривая 2) и  (кривая 1) соответственно.

 

Заключение

Приведено описание сигнальных конструкций на основе последовательных турбо-кодов с использованием сигналов с относительной фазовой манипуляцией и совокупности блоковых кодов, соответствующих базисным функциям Уолша-Адамара. Эти сигнальные конструкции перспективны для использования в системах передачи информации по нестационарным каналам с межсимвольным программным переключением частоты. Приведены алгоритмы их итеративного некогерентного приема и результаты компьютерного моделирования для сигнальных конструкций с информационным объемом ≈1000 битов и с различными информационными скоростями.

Показано, что рассматриваемые сигнальные конструкция характеризуются большей помехоустойчивостью для АБГШ канала по отношению к известной сигнальной конструкции [18], формируемой на основе сверточного кода - энергетический выигрыш при вероятности ошибки на бит для  превышает 0.1 дБ. Показано также, что рассматриваемые сигнальные конструкции обеспечивают большую помехоустойчивость при некогерентном приеме по отношению к сравниваемой известной сигнальной конструкции для АБГШ многолучевого канала с Релеевским распределением амплитуды сигналов - энергетический выигрыш для  достигает 4.2 дБ.

 

Работа выполнена при поддержке РФФИ (№16-07-00746).

 

Литература

1. Финк Л.М. Теория передачи дискретных сообщений. М.:Сов.радио. 1970.

2. Коржик В.И., Финк Л.М., Щелкунов Н.Н. Расчет помехоустойчивости систем передачи дискретных сообщений. М.: Радио и связь, 1981.

3. Сакалема Д.Ж. Подвижная радиосвязь. М.: Горячая линия-Телеком. 2012.

4. Яковлев О.И., Якубов В.П., Урядов В.П., Павельев А.Г. Распространение радиоволн. М.: ЛЕНАНД. 2009.

5. Немировский А.С. Борьба с замираниями при передаче аналоговых сигналов. М.:Радио и связь. 1984.

6. Сорочинский М.В., Кузнецов О.О., Назаров Л.Е. Некоторые модели каналов передачи сигналов и экспериментальное определение их параметров.// Электронная техника. Выпуск 2(482). 2003. С.119-124.

7. Keskinen M. J., Kullstam A. Updated UHF Scintillation and Channel Parameters for MUOS. NRL/PAIRCOM Memorandum Report for SPAWAR PMW-146. 2000. 30 March.

8. Назаров Л.Е. Некогерентный посимвольный прием сигналов, соответствующих двоичным блоковым кодам.// Радиотехника и электроника. 2003. Т.48. N7. С.818-823.

9. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема.// Радиотехника и электроника. 2010. Т. 55. №10. стр. 1193-1199.

10. Johnson S.J. Iterative Error Correction: Turbo, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge: Univ. Press, 2010.

11. Борисов В.И., Зинчук В.М. Помехозащищенность систем радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки радиочастоты. М.: Радио и связь. 2000.

12. Назаров Л.Е., Шишкин П.В., Батанов В.В. Алгоритмы итеративного некогерентного приема сигналов на основе последовательных турбо-кодов и сигналов Уолша при передаче по нестационарным каналам. // Радиотехника и электроника. 2016. Т.61. №4. Стр. 366-372

13. Назаров Л.Е., Шишкин П.В. Алгоритмы некогерентного приема сигнально-кодовых конструкций на основе блоковых турбо-кодов.// Журнал радиоэлектроники, http://jre.cplire.ru/jul12/2/text.pdf. 2012. №7.

14. Valenti M.C. Iterative demodulation and decoding of turbo-coded M-ary noncoherent orthogonal modulation.// IEEE Journal on Selected Areas in Communications. 2005. Vol. 23, N9. P.1739-1747.

15. Назаров Л.Е Итеративный некогерентный прием турбо-кодов на основе двоичных блоковых кодов.// Радиотехника и электроника. 2005. Т.50. №3 Стр.315-320.

16. Назаров Л.Е. Некогерентный посимвольный прием сигналов, соответствующих двоичным блоковым кодам.// Радиотехника и электроника. 2003. Т.48. N7. С.818-823.

17. Jing Li., Narayanan K.R., Georghiades .N. Product accumulate codes: a class of codes with near-capacity performance and low decoding complexity.// IEEE Transactions on Information Theory. 2004. V.50. N1. P.31-46.

18. Phoel W.G. Iterative demodulation and decoding for protected satellite communications.// Lincoln Laboratory Journal. 2005. V.15. N1. P.79-96.

19. Ахмед Н., Рао К.Р. Ортогональные преобразования при цифровой обработке сигналов. М.:Связь. 1980. 248 с.

20. Benedetto S., Divsalar D., Montorsi G., Pollara F. Serial concatenation of interleaved codes: performance analysis, design, and iterative decoding.// IEEE Transactions on Information Theory. 1998. V.44. N3. P.909-926.

 

References

1. Fink L.M. Teoriya peredachi discretnykh soobschenii. [The theory of discrete message transmission]. Moscow, Sov. Radio Publ. 1970. (In Russian)

2. Korzhik V.I., Fink L.M., Schelkunov N.N. Raschet pomekhoustoichivosti system peredachi diskretnykh soobschenii. [Noise immunity calculation for the systems of discrete message transmission]. Moscow, Radio I Svyaz Publ. 1981. (In Russian)

3. Sakalema D.Zh. Podvizhnaya radiosvyaz.[Mobile radio telecommunicstions]. Moscow, Goryachaya Linia-Telecom Publ. 2012. (In Russian)

4. Yakovlev O.I., Yakubov V.P., Uryadov V.P., Pavelyev A.G. Rasprostranenie radiovoln. [Propagation of radio waves]. Moscow, LENAND Publ. 2009. (In Russian)

5. Nemirovskii A.S. Borba s zamiraniyami pri peredache analogovykh signalov. [The mitigation of fading for analog signal transmission]. Moscow, Radio I Svyaz Publ. 1984. (In Russian)

6. Sorochinskii M.V., Kuznetsov О.O., Nazarov L.E. Some models of signal transmission channels and experimental determination of its parameters. Elektronnaya tekhnika – Electronics engineering. 2003, 2(482), pp. 119-124. (In Russian)

7. Keskinen M. J., Kullstam A. Updated UHF Scintillation and Channel Parameters for MUOS. NRL/PAIRCOM Memorandum Report for SPAWAR PMW-146. 2000. 30 March.

8. Nazarov L.E. Incoherent Symbol-by-Symbol Reception of Signals Corresponding to Binary Block Codes. Journal of Communications Technology and Electronics, 2003, Vol. 48, No. 7, pp.744-750.

9. Nazarov L.E., Golovkin I.V. Serial Turbo Codes with a Low Complexity of Reception Algorithms. Journal of Communications Technology and Electronics, 2010, Vol. 55, No.10, pp. 1115-1122. DOI: 10.1134/S1064226910100049

10. Johnson S.J. Iterative Error Correction: Turbo, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge: Univ. Press, 2010.

11. Borisov V.I., Zichuk V.M. Pomekhozaschischennost system radiosvyazi s rasshireniem spectra signalov metodom psevdosluchainoi perestroiki radiochastoty. [Noise immunity of radio communication systems with frequency-hopping spread]. Moscow, Radio I Svyaz Publ. 2000. (In Russian)

12. Nazarov L.E., Shishkin P.V, Batanov V.V. Algorithms for Noncoherent Iterative Reception of Signals Based on Serial Turbo Codes and Walsh Signals during Transmission over Nonstationary Channels. Journal of Communications Technology and Electronics, 2016, Vol. 61, No.4, pp. 414-423. DOI: 10.1134/S1064226916040082

13. Nazarov L.E., Shishkin P.V. Noncoherent decoding of block turbo codes. Zhurnal radioelectroniki - Journal of Radio Electronics, 2012, No. 7 (In Russian)  Available at http://jre.cplire.ru/jul12/2/text.pdf.

14. Valenti M.C. Iterative demodulation and decoding of turbo-coded M-ary noncoherent orthogonal modulation. IEEE Journal on Selected Areas in Communications. 2005. Vol. 23, No. 9. pp.1739-1747. DOI: 10.1109/JSAC.2005.853794

15. Nazarov L.E. Iterative Incoherent Reception of Turbo Codes Based on Binary Block Codes. Journal of Communications Technology and Electronics, 2005, Vol. 50, No.3, pp. 292-298.

16. Nazarov L.E. Incoherent Symbol-by-Symbol Reception of Signals Corresponding to Binary Block Codes. Journal of Communications Technology and Electronics, 2003, Vol. 48, No.7, pp. 744-750.

17. Jing Li., Narayanan K.R., Georghiades N. Product accumulate codes: a class of codes with near-capacity performance and low decoding complexity. IEEE Transactions on Information Theory. 2004. Vol. 50. No. 1. pp. 31-46. DOI: 10.1109/TIT.2003.821995

18. Phoel W.G. Iterative demodulation and decoding for protected satellite communications. Lincoln Laboratory Journal. 2005. Vol. 15. No. 1. pp. 79-96.

19. Akhmed N., Rao K.R. Ortogonalnye preobrazovaniya pri tsifrovoy obrabotke signalov. [Orthogonal transformations in digital signal processing]. Moscow: Svyaz Publ. 1980. 248 p. (In Russian)

20. Benedetto S., Divsalar D., Montorsi G., Pollara F. Serial concatenation of interleaved codes: performance analysis, design, and iterative decoding. IEEE Transactions on Information Theory. 1998. Vol. 44. No. 3. pp. 909-926. DOI: 10.1109/18.669119