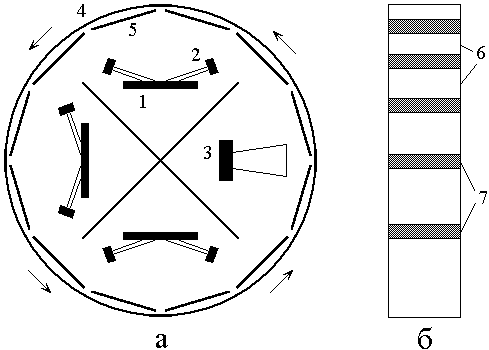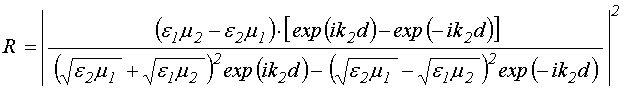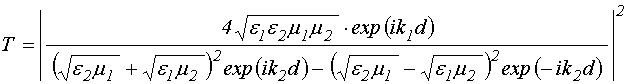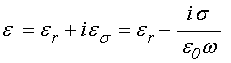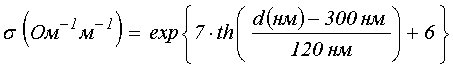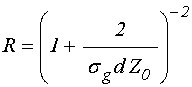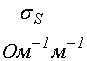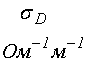УДК 537.874; 537.624
СТАТИЧЕСКАЯ И ДИНАМИЧЕСКАЯ ПРОВОДИМОСТЬ НАНОГРАНУЛИРОВАННЫХ ПЛЕНОК «МЕТАЛЛ-ДИЭЛЕКТРИК»
И. В. Антонец1, В. С. Власов1, Л. Н. Котов1, О. А. Кирпичёва1, Е. А. Голубев2, Ю. Е. Калинин3, А. В. Ситников3, В. Г. Шавров4, В. И. Щеглов4
1 Сыктывкарский государственный университет
2Институт геологии Коми НЦ Уро РАН
3Воронежский государственный технический университет
4Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья поступила в редакцию 15 мая 2016 г.
Аннотация. Методом ионно-лучевого напыления на
лавсановой подложке большой площади (до ![]() )
выращены аморфные наногранулированные пленки типа «металл-диэлектрик» следующих
составов:
)
выращены аморфные наногранулированные пленки типа «металл-диэлектрик» следующих
составов: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . По
площади пленок исследовано распределение толщины, концентрации и относительного
объема металлической фазы, а также статической и динамической проводимости.
Отмечено сильное (до двух порядков и более) превышение динамической
проводимости над статической, имеющее место на пленках с диэлектрической
матрицей
. По
площади пленок исследовано распределение толщины, концентрации и относительного
объема металлической фазы, а также статической и динамической проводимости.
Отмечено сильное (до двух порядков и более) превышение динамической
проводимости над статической, имеющее место на пленках с диэлектрической
матрицей ![]() , обусловленное крайне низкой статической
проводимостью диэлектрической фазы (порядка
, обусловленное крайне низкой статической
проводимостью диэлектрической фазы (порядка ![]() ).
Полученные результаты интерпретированы на основе модели внутригранулярных
токов.
).
Полученные результаты интерпретированы на основе модели внутригранулярных
токов.
Ключевые слова: тонкие пленки, нанокомпозит металл-диэлектрик, отражение электромагнитных волн.
Abstract. By means of ion-beams
raising onto lavsan foundation of great area (up to ![]() ) the nano-granulated films
by type of “metal-dielectric” having composition:
) the nano-granulated films
by type of “metal-dielectric” having composition: ![]() ,
, ![]() ,
, ![]() ,
, ![]() are grown. Onto the
films area it is investigated the distribution of thickness, concentration and
relative value of metal-phase and also static and dynamic conductivity. It is
found the great (on two order and more) exceeding of dynamic conductivity over
static conductivity taking place on films with dielectric matrix
are grown. Onto the
films area it is investigated the distribution of thickness, concentration and
relative value of metal-phase and also static and dynamic conductivity. It is
found the great (on two order and more) exceeding of dynamic conductivity over
static conductivity taking place on films with dielectric matrix ![]() , caused by low static
conductivity of dielectric phase (about
, caused by low static
conductivity of dielectric phase (about ![]() ). The received results are explained
by the model of intergranular currents.
). The received results are explained
by the model of intergranular currents.
Key words: thin films, nanocomposit metal-dielectric, electromagnetic wave reflection.
Введение
Внимание исследователей к наногранулированным композитам «металл-диэлектрик» в последнее время нарастает быстрыми темпами [1-4]. Значительный интерес представляют композиты, содержащие магнитные наночастицы железа и кобальта, что придает им уникальные анизотропные и структурные свойства [5-7].
Для создания новых классов устройств обработки информации в диапазоне СВЧ весьма перспективными являются метаматериалы – композиты, состоящие из множества отдельных элементов, собранных в определенном порядке. Важное место здесь занимают фотонные и магнонные кристаллы, проявляющие «левые» волноведущие свойства [8-13].
Особым классом таких материалов являются наноструктурные гранулированные металл-диэлектрические пленки, распределение гранул внутри которых, в отличие от упорядоченного в кристаллах, носит хаотический характер [14]. Включение ферромагнитного металла в состав таких пленок обеспечивает гигантское магнитосопротивление [15] в сочетании с высоким уровнем поглощения СВЧ сигнала [16].
Высокое разнообразие прикладных возможностей таких пленок стимулирует изучение их физических свойств, к которым относятся как процессы намагничивания, так и механизмы электропроводности [5-7, 17, 18].
Для интерпретации электрических свойств гранулированных нанокомпозитов предложены модели прыжковой проводимости [19], активированного [20-22] и резонансного туннелирования [23, 24]. В области СВЧ наблюдается аномальное уширение линии ФМР [25] и особенности электронного транспорта, выявляемые методами спин-волновой спектроскопии [26-28].
Значительный интерес представляет существенное отличие электрической проводимости таких пленок, измеряемой по отражению сигнала СВЧ, от проводимости статической, измеряемой на постоянном токе.
На различие динамической и статической проводимостей нанопленок, по-видимому, впервые было указано в работах [29, 30], где исследовались аморфные пленки железа, толщиной до 800 нм, имеющие кластерный характер. Было отмечено, что в диапазоне 8-12 ГГц динамическая проводимость в таких пленках может превышать статическую до полутора-двух раз.
В работах [31,
32],
посвященных наногранулированным пленкам составов ![]() и
и ![]() , имеющих толщину
, имеющих толщину ![]() ,
было отмечено превышение динамической проводимости над статической до четырех
раз. Для интерпретации наблюдаемой зависимости удельного сопротивления от
концентрации проводящей фазы предложен топологический механизм формирования
статической проводимости, учитывающий кластерную структуру пленок. Для
объяснения превышения динамической проводимости над статической предложены
механизмы емкостного шунтирования, эффективной диэлектрической проницаемости и
внутрикластерных токов.
,
было отмечено превышение динамической проводимости над статической до четырех
раз. Для интерпретации наблюдаемой зависимости удельного сопротивления от
концентрации проводящей фазы предложен топологический механизм формирования
статической проводимости, учитывающий кластерную структуру пленок. Для
объяснения превышения динамической проводимости над статической предложены
механизмы емкостного шунтирования, эффективной диэлектрической проницаемости и
внутрикластерных токов.
Впервые механизм емкостного шунтирования кластеров в диапазоне СВЧ рассматривался в работе [33] с целью интерпретации некоторой частотной зависимости сигнала отражения в диапазоне частот 10-25 ГГц (увеличения коэффициента отражения до полутора раз), однако последующие эксперименты, выполненные в диапазоне 4-40 ГГц [34, 35] заметной частотной зависимости не выявили.
В работах [35,
36] при
исследовании пленок состава ![]() наблюдалось
гигантское различие динамической и статической проводимостей, достигающее
четырех порядков.
наблюдалось
гигантское различие динамической и статической проводимостей, достигающее
четырех порядков.
Для интерпретации столь высокого превышения динамической проводимости над статической предложены механизмы емкостного шунтирования, эффективной диэлектрической проницаемости, внутригранулярных токов, дипольного излучения.
Путем сравнительного качественного анализа перечисленных механизмов сделан вывод о преобладающей роли механизма внутригранулярных токов. В качестве возможной причины огромной величины превышения выдвинута гипотеза о роли плохо проводящего циркония, использование окисла которого в качестве матрицы приводит к резкому падению ее статической проводимости при сохранении динамической проводимости за счет металлических кластеров на прежнем уровне. То есть значительное различие проводимостей обусловлено наличием циркония одновременно как в металлической, так и в диэлектрической фазах.
Наиболее подробно механизм внутригранулярных токов рассмотрен в работе [34]. Предложена модель планарного распределения гранул внутри пленки, на основе которой показано, что поля вторичных волн, создаваемых волной, падающей на слой гранул, приближаются по величине к полю падающей волны.
На основе предложенной модели рассчитан коэффициент отражения волны от одного слоя гранул. В формировании вторичных волн выявлена определяющая роль поверхностных слоев, обусловленная взаимной компенсацией полей соседствующих гранул.
Модель обобщена на случай пленки, содержащей значительное количество слоев. Рассмотрены особенности формирования отраженной и проходящей волн в предельных случаях тонкой и толстой пленки.
Результаты расчета по предложенной модели сопоставлены с экспериментами по отражению волн от пленок. Выявлено хорошее соответствие как по порядку величины коэффициента отражения, так и по связи его с толщиной пленок. Результаты эксперимента интерпретированы с учетом механизма компенсации вторичных волн. Предсказано и выявлено в эксперименте существование критического значения толщины пленки, определяющего порог резкого роста коэффициента отражения, обусловленного механизмом раскомпенсации.
В работе [37] полученные результаты использованы для рассмотрения отражения и прохождения волны СВЧ через пленку с помощью механизма переотражений [38-40]. На основе модели внутригранулярных токов получены амплитудные коэффициенты отражения и прохождения волны, выраженные через удельную проводимость материала гранул. Полученные численные значения коэффициентов объясняют наблюдаемое в эксперименте значительное превышение динамической проводимости пленок над статической.
В работе [41] исследованы
пленки того же состава, что и в [34, 35,
37], но имеющие сравнительно большую толщину
– до ![]() . Показано, что в этих условиях
динамическая проводимость превышает статическую не более чем на один-два порядка,
в отличие от четырех порядков в работах [34,
35, 37]. В качестве механизма,
ответственного за уменьшение соотношения проводимостей в этом случае, отмечено влияние
большой толщины пленок, приводящей к смыканию металлических гранул в большие
кластеры, что увеличивает статическую проводимость за счет перколяции.
. Показано, что в этих условиях
динамическая проводимость превышает статическую не более чем на один-два порядка,
в отличие от четырех порядков в работах [34,
35, 37]. В качестве механизма,
ответственного за уменьшение соотношения проводимостей в этом случае, отмечено влияние
большой толщины пленок, приводящей к смыканию металлических гранул в большие
кластеры, что увеличивает статическую проводимость за счет перколяции.
Таким образом, можно полагать, что исследование соотношения между статической и динамической проводимостями в гранулированных пленках выполнено со значительной полнотой и разнообразием.
Однако следует отметить,
что оно не является исчерпывающим. Так более или менее подробно в широком
диапазоне толщин и проводимостей исследованы пленки лишь одного состава ![]() , тогда как пленки других составов
рассмотрены только при больших толщинах. При этом установлено, что уменьшение
толщины приводит к увеличению соотношения проводимостей, так что можно ожидать,
что и другие составы при малых толщинах проявят аналогичные свойства.
, тогда как пленки других составов
рассмотрены только при больших толщинах. При этом установлено, что уменьшение
толщины приводит к увеличению соотношения проводимостей, так что можно ожидать,
что и другие составы при малых толщинах проявят аналогичные свойства.
Из заключения о решающей роли плохой проводимости циркония можно предположить, что замена циркония лучше проводящим ингредиентом, например кальцием, должна привести к уменьшению превышения динамической проводимости над статической, что и следует выяснить.
Таким образом, в качестве целей ближайшего исследования можно наметить исследование пленок других составов в случае малых толщин, а также использование в качестве матрицы других диэлектриков, проводимость которых отлична от проводимости окисла циркония. Таким исследованиям и посвящена настоящая работа.
1. Технология выращивания пленок
В работе исследовались
пленки составов ![]() , где
, где ![]() –
металлическая (проводящая) фаза
–
металлическая (проводящая) фаза ![]() , образующая гранулы, а
, образующая гранулы, а
![]() – диэлектрическая фаза
– диэлектрическая фаза ![]() ,
, ![]() ,
, ![]() ,
, ![]() , формирующая
матрицу.
, формирующая
матрицу.
Пленки были выращены в ВГТУ (Воронеж, Россия) Ю.Е.Калининым и А.В.Ситниковым методом ионно-лучевого напыления на установке, собранной на основе вакуумного напылительного поста УВН-2М [5, 7].
Схема установки показана
на рис.1 [7]. Ее основу составляла цилиндрическая вакуумная камера (рис.1а),
разделенная на четыре симметричных сектора, в трех из которых располагались
мишени 1 с источниками ионно-лучевого распыления 2, а в четвертом – источник
ионного травления 3. Вдоль цилиндрической образующей камеры с помощью
подложкодержателя 4 закреплялись до 12 подложек 5 размерами до ![]() .
.
Рис.1. Схема установки напыления (а) и составной мишени (б).
1 – мишень, 2 – источник
ионно-лучевого распыления, 3 – источник ионного травления,
4 –
подложкодержатель, 5 – подложка, 6 – материал мишени, 7 – диэлектрические
пластины.
Структура мишеней
показана на рис.1б. В общем случае мишени представляли собой металлические
пластины 6 состава ![]() размерами
размерами ![]() , частично перекрытые пластинами из
диэлектрика 7 требуемого состава, расстояние между которыми по длине мишени
плавно возрастало.
, частично перекрытые пластинами из
диэлектрика 7 требуемого состава, расстояние между которыми по длине мишени
плавно возрастало.
В процессе напыления подложкодержатель совершал вращение вокруг оси цилиндрической камеры в направлении, показанном стрелками со скоростью от 1 до 0.001 об/мин.
Неравномерное расположение диэлектрических пластин по длине мишени позволяло получить пленки, содержание металлической фазы в которых по координате менялось.
Большая протяженность
подложки по длине относительно источника распыления позволяла в одном цикле
получать пленки, толщина которых на протяжении подложки менялась непрерывным
образом, в частности, к краям подложки была меньше, чем на ее середине.
Дополнительно толщина пленок регулировалась с помощью V-образного экрана, устанавливаемого между одной из мишеней и
подложкой [7]. Такая методика позволяла в одном технологическом цикле на
протяженной подложке формировать слой композита с непрерывно меняющейся
толщиной от ![]() до
до![]() . Для
последующих измерений из общей подложки вырезались образцы размером до
. Для
последующих измерений из общей подложки вырезались образцы размером до ![]() , что обеспечивало полнее перекрытие окна
волновода панорамного спектрометра, используемого при СВЧ измерениях (описан
далее).
, что обеспечивало полнее перекрытие окна
волновода панорамного спектрометра, используемого при СВЧ измерениях (описан
далее).
В качестве подложки
использовалась полимерная пленка из лавсана (![]() ) толщиной
) толщиной
![]() , площадью
, площадью ![]() . С
целью стабилизации аморфной структуры металлической фазы пленок к атомам железа
и кобальта было добавлено
. С
целью стабилизации аморфной структуры металлической фазы пленок к атомам железа
и кобальта было добавлено ![]() аморфизатора –
циркония. Выбор материалов матрицы
аморфизатора –
циркония. Выбор материалов матрицы ![]() ,
, ![]() ,
, ![]() и
и ![]() был обусловлен требованием термической
стабильности в широком диапазоне температур.
был обусловлен требованием термической
стабильности в широком диапазоне температур.
Применение многолучевой методики в сочетании с экранированием позволило получить пленки большой площади с контролируемой толщиной в широком диапазоне концентрации металлической фазы.
2. Технологические параметры пленок
В работе исследовались восемь серий пленок наногранулированных композитов следующих составов:
![]() (серии
№1 и №2),
(серии
№1 и №2),
![]() (серия
№3),
(серия
№3),
![]() (серии
№4 и №5),
(серии
№4 и №5),
![]() (серии
№6, №7, №8).
(серии
№6, №7, №8).
В морфологическом
отношении пленки представляли собой металлические гранулы ![]() , вкрапленные в диэлектрическую матрицу
окисла
, вкрапленные в диэлектрическую матрицу
окисла ![]() ,
, ![]() ,
, ![]() или фторида
или фторида ![]() ,
причем концентрация металлической фазы
,
причем концентрация металлической фазы ![]() составляла
от
составляла
от ![]() до
до ![]() .
.
Порогу перколяции
соответствовала концентрация ![]() , ниже которой пленки
имели преимущественно диэлектрический характер, а выше – преимущественно
металлический.
, ниже которой пленки
имели преимущественно диэлектрический характер, а выше – преимущественно
металлический.
Основные технологические параметры исследованных пленок приведены в таблице №1.
Таблица №1. Технологические параметры пленок.
|
Номер Серии |
Состав матрицы |
Металлическая фаза |
Толщина (нм) |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
Точный состав композитов определялся электронно-зондовым рентгеновским микроанализом с помощью микроскопа JSM-6400, снабженного детектором вторичных электронов R-BSE [5, 31].
Толщина пленок измерялась
по изображениям поверхности торца пленок, полученных с помощью сканирующего
электронного микроскопа (VEGA 3
LMH, катод – ТЕСКАН). Вдоль торца
отмечались 15 рассредоточенных точек, полученные значения толщины в которых
затем усреднялись. Измеренная толщина составляла![]() с
отклонением порядка
с
отклонением порядка ![]() .
.
Гранулированный характер
пленок контролировался методом просвечивающей электронной микроскопии (путем
как непосредственного наблюдения, так и дифракции электронов [42-44]) на
контрольных образцах, выполненных на подложках из ![]() в виде
пленок толщиной до
в виде
пленок толщиной до ![]() (для обеспечения возможности
просвечивания). Напыление контрольных пленок проводилось в тех же условиях, что
и основных, но за более короткое время. Типичная скорость напыления была около
(для обеспечения возможности
просвечивания). Напыление контрольных пленок проводилось в тех же условиях, что
и основных, но за более короткое время. Типичная скорость напыления была около ![]() . При этом время напыления основных пленок
составляло от 2 до 24 мин, а контрольных – не более 4 мин.
. При этом время напыления основных пленок
составляло от 2 до 24 мин, а контрольных – не более 4 мин.
Аморфный характер металлических гранул определялся по высокой степени размытия кольцевых дифракционных гало на электронных микрофотографиях [7, 45].
Топография поверхности
пленок исследовалась с помощью атомно-силового микроскопа по методике,
описанной в [29, 30, 46]. Использовался микроскоп ARIS-3500 с максимальным
полем сканирования ![]() (Burleigh Instrument Co., США).
В качестве зондов использовались стандартные кремниевые кантилеверы (Burleigh)
пирамидальной формы с радиусом закругления кончика
(Burleigh Instrument Co., США).
В качестве зондов использовались стандартные кремниевые кантилеверы (Burleigh)
пирамидальной формы с радиусом закругления кончика ![]() и
жесткостью
и
жесткостью![]() . В большинстве случаев пленки имели
зернистый характер, образованный кластерами, содержащими множество гранул,
размер которых составлял
. В большинстве случаев пленки имели
зернистый характер, образованный кластерами, содержащими множество гранул,
размер которых составлял ![]() . На всех пленках наблюдался
четко выраженный зернистый характер поверхности, подобный описанному в [29,
30, 46], размер зерен составлял от
. На всех пленках наблюдался
четко выраженный зернистый характер поверхности, подобный описанному в [29,
30, 46], размер зерен составлял от ![]() до
до ![]() и увеличивался с увеличением толщины
пленки.
и увеличивался с увеличением толщины
пленки.
3. Измерение статической проводимости
Главной задачей настоящей работы является сравнение статической проводимости пленок, измеряемой на постоянном токе, с проводимостью динамической, измеряемой в диапазоне СВЧ. Статическая проводимость определялась как величина, обратная удельному сопротивлению пленок. Измерение такого сопротивления проводилось на постоянном токе двухзондовым потенциометрическим методом с помощью тераомметра (ЕФ-13А), подобным описанному в работах [33, 35, 46]. Контакты представляли собой два прямолинейных параллельных друг другу проводника длиной около 20 мм, перекрывавшие всю ширину пленки. Расстояние между контактами могло регулироваться от 5 до 20 мм. В эксперименте определялось абсолютное сопротивление участка пленки между контактами, после чего по измеренной заранее толщине пленки с учетом площади участка между контактами определялось удельное сопротивление материала пленки, из которого затем в качестве обратной величины получалась удельная проводимость.
4. Измерение коэффициента отражения
Динамическая проводимость определялась путем измерения коэффициента отражения волны СВЧ сигнала на установке, схема которой показана на рис.2.
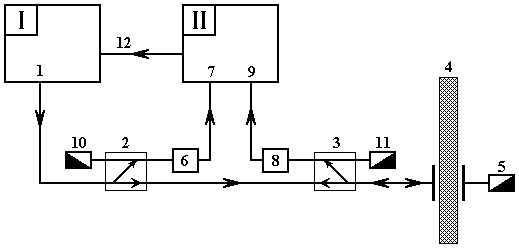
Рис.2. Схема экспериментальной установки для измерения отражения сигнала СВЧ от пленок.
I – генератор II – индикатор
1 – выход генератора; 2, 3 – направленные
ответвители; 4 – исследуемый образец;
5, 10, 11 – согласованные нагрузки; 6,
8 – детекторы; 7, 9 – входы индикатора; 12 – цепь обратной связи.
Сигнал с выхода 1 генератора качающейся частоты I, распространяясь в направлении, показанном стрелками, минуя два направленных ответвителя 2 и 3, поступает на исследуемый образец 4, отражаясь от которого распространяется в обратном направлении. Проходящий через образец сигнал поглощается согласованной нагрузкой 5. Сигнал, ответвляемый первым ответвителем 2, детектируется детектором 6, после чего поступает на первый вход 7 индикатора II. Сигнал, ответвляемый вторым ответвителем 3, после детектирования детектором 8 поступает на второй вход 9 индикатора II. Сигналы, отраженные от детекторов 6 и 8, поглощаются согласованными нагрузками 10 и 11. Сигнал, распространяющийся в обратном направлении после ответвителя 3, поступая на выход генератора I, поглощается там встроенным вентилем. Цепь 12 осуществляет обратную связь между индикатором и генератором и предназначена для выравнивания амплитуды генерируемого сигнала по диапазону частот.
Отражение электромагнитных волн от пленок исследовалось в диапазоне 8-70 ГГц с помощью комплекта волноводных СВЧ спектрометров, включавших в себя генератор качающейся частоты (ГКЧ-61, 65, 68) в сочетании с индикатором КСВН и ослабления (Я2Р-67). Измерение коэффициента отражения пленок проводилось по методике, аналогичной описанной в работах [29, 30] для металлических пленок. В отличие от работы [33], где коэффициент отражения измерялся по напряжению, в настоящей работе, подобно [29, 30], коэффициент отражения измерялся по мощности. Отражение волн СВЧ от материала подложки не превышало 5%.
Подробные измерения показали, что описываемые далее характеристики динамической проводимости в исследуемом диапазоне 8-70 ГГц от частоты практически не зависят, что согласуется с данными работы [37], а также приведенных там ссылок. Поэтому описываемые далее результаты, если частота точно не указана, можно относить к низшей частоте диапазона – 8 ГГц.
5. Методика сравнения статической и динамической проводимостей
Рассмотрим теперь
методику сравнения статической и динамической проводимостей на примере пленок
серии №4 (состав ![]() ). Более подробно формирование
образцов будет рассмотрено в следующем разделе, здесь же опишем общую схему
сравнения проводимостей, подобную применявшейся в работах [34-36]. В качестве
переменного параметра на данном этапе выберем толщину пленок. Сравнение проводимостей
при изменении концентрации металлической фазы проводится аналогично.
). Более подробно формирование
образцов будет рассмотрено в следующем разделе, здесь же опишем общую схему
сравнения проводимостей, подобную применявшейся в работах [34-36]. В качестве
переменного параметра на данном этапе выберем толщину пленок. Сравнение проводимостей
при изменении концентрации металлической фазы проводится аналогично.
Как отмечено в предыдущем разделе, промежуточным инструментом для получения динамической проводимости является измерение коэффициента отражения сигнала СВЧ от пленок. В качестве вспомогательных данных можно рассматривать также измерение коэффициента прохождения.
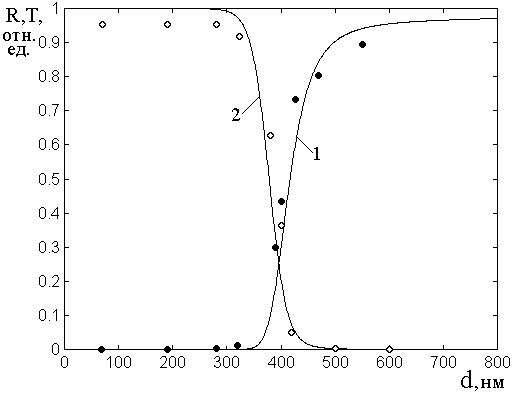
На рис.3 показаны
зависимости энергетических коэффициентов отражения ![]() и
прохождения
и
прохождения ![]() от толщины пленки
от толщины пленки ![]() .
Точки – результаты эксперимента, кривые 1-4 построены по формулам [37,
47-49]:
.
Точки – результаты эксперимента, кривые 1-4 построены по формулам [37,
47-49]:
где ![]() ,
, ![]() ,
, ![]() –
проницаемости и волновое число в свободном пространстве,
–
проницаемости и волновое число в свободном пространстве, ![]() ,
, ![]() ,
, ![]() – проницаемости и волновое число в
пленке,
– проницаемости и волновое число в
пленке, ![]() – толщина пленки.
– толщина пленки.
Волновое число определялось по формуле:
Проводимость пленки ![]() учитывалась в виде мнимой добавки к
диэлектрической проницаемости с помощью формулы:
учитывалась в виде мнимой добавки к
диэлектрической проницаемости с помощью формулы:
где ![]() –
диэлектрическая проницаемость пленки в отсутствие проводимости,
–
диэлектрическая проницаемость пленки в отсутствие проводимости, ![]() – частота,
– частота, ![]() -
диэлектрическая постоянная. В расчетах полагалось: в свободном пространстве:
-
диэлектрическая постоянная. В расчетах полагалось: в свободном пространстве: ![]() ,
, ![]() ,
, ![]() , в материале пленок в отсутствие
проводимости:
, в материале пленок в отсутствие
проводимости: ![]() ,
, ![]() ,
, ![]() .
.
Рис.3. Зависимости коэффициента отражения (1) и прохождения (2) от толщины пленок.
При построении кривых 1 и
2, приведенных на рис.3, входящая в формулу (4) проводимость ![]() рассчитывалась по эмпирической формуле,
впервые полученной в работе [37]:
рассчитывалась по эмпирической формуле,
впервые полученной в работе [37]:
Для получения
динамической проводимости из данных, приведенных на рис.3, надо формулу (1)
«обернуть», то есть не по (5) получить зависимость (1), а исходя из (1) найти
зависимость типа ![]() . Аналитически такое выражении
проводимости
. Аналитически такое выражении
проводимости ![]() через коэффициент отражения
через коэффициент отражения ![]() в общем случае вряд ли возможно, что и
обусловило использование эмпирической формулы (5), полученной из условия
максимального совпадения кривой 1 с данными эксперимента.
в общем случае вряд ли возможно, что и
обусловило использование эмпирической формулы (5), полученной из условия
максимального совпадения кривой 1 с данными эксперимента.
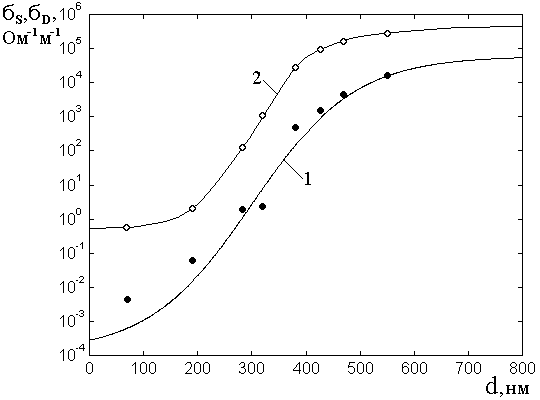
Рис.4. Зависимости статической (1) и динамической (2) проводимостей от толщины пленки (серия №4).
Полученные в результате зависимости статической и динамической проводимости от толщины пленки приведены на рис.4. Кривая 1, соответствующая статической проводимости, построена по эмпирической формуле, в основе которой под знаком экспоненты лежит гиперболический тангенс:
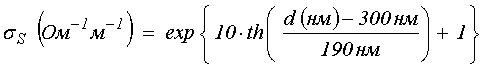 . (6)
. (6)
В этой формуле числовые параметры подобраны из условия максимального соответствия экспериментальным точкам.
Кривая 2, соответствующая динамической проводимости, построена по сходной формуле, имеющей однако несколько другие числовые параметры, близкие к таковым в формуле (5):
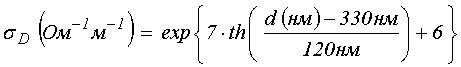 .
(7)
.
(7)
Можно
видеть, что так определенная динамическая проводимость ![]() превышает
статическую
превышает
статическую ![]() тем сильнее, чем толщина пленки меньше.
Так при толщинах
тем сильнее, чем толщина пленки меньше.
Так при толщинах ![]() такое превышение составляет
несколько больше одного порядка величины, тогда как при толщинах
такое превышение составляет
несколько больше одного порядка величины, тогда как при толщинах ![]() возрастает до двух порядков и более.
Причина и механизм такого превышения разбирались в работах [34-36], поэтому на
данном этапе настоящего изложения подробно не обсуждаются.
возрастает до двух порядков и более.
Причина и механизм такого превышения разбирались в работах [34-36], поэтому на
данном этапе настоящего изложения подробно не обсуждаются.
6. Общая геометрия совокупности образцов
Рассмотрим теперь общие
свойства исследованных в настоящей работе образцов, для чего начнем с их геометрии.
В исходном состоянии пленки выращивались на подложке в виде одного большого
листа на лавсане размером ![]() . Этот лист разрезался
сначала вдоль размера в
. Этот лист разрезался
сначала вдоль размера в ![]() на
на ![]() полосок, каждая шириной по
полосок, каждая шириной по ![]() , после чего каждая полоска разрезалась
поперек еще на
, после чего каждая полоска разрезалась
поперек еще на ![]() частей, длиной каждая по
частей, длиной каждая по ![]() . Таким образом, каждый образец (ячейка)
имел размер
. Таким образом, каждый образец (ячейка)
имел размер ![]() . Общая геометрия разрезания первоначального
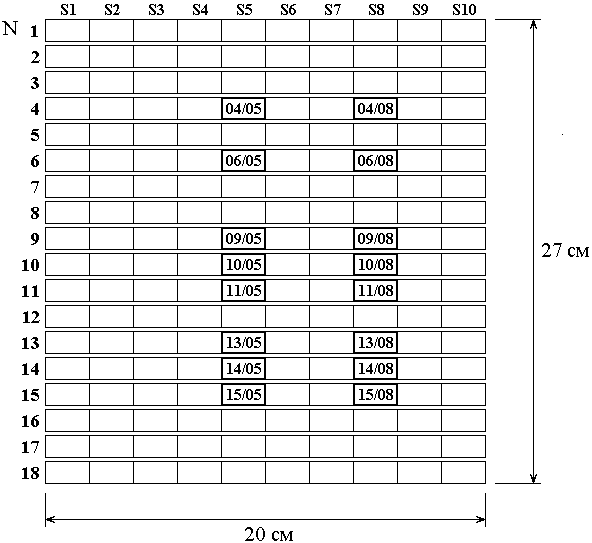
листа иллюстрируется рис.5.
. Общая геометрия разрезания первоначального
листа иллюстрируется рис.5.
Рис.5. Геометрия разрезания исходной подложки. Утолщенными рамками обведены ячейки, исследуемые далее в разделе №8 (серия №7).
Полоски были
пронумерованы номерами ![]() от 1 до 18, ячейки – номерами
от 1 до 18, ячейки – номерами ![]() от 1 до 10. При обращении к образцам
сначала записывался номер полоски, затем – номер ячейки в виде: «образец или
ячейка № N/S».
от 1 до 10. При обращении к образцам
сначала записывался номер полоски, затем – номер ячейки в виде: «образец или
ячейка № N/S».
Благодаря технологии
экранирования (раздел №1), толщина пленки по краям исходного листа подложки получалась
относительно малой – до ![]() , а в середине –
большой – до
, а в середине –
большой – до ![]() . При этом концентрация проводящей фазы
. При этом концентрация проводящей фазы ![]() с увеличением номера полоски
с увеличением номера полоски ![]() возрастала от
возрастала от ![]() до
до ![]() .
.
В направлении поперек
полоски, то есть при сохранении номера ячейки ![]() содержание
металла (как составной части проводящей фазы) менялось весьма значительно.
Например в случае серии №7 для полоски №3 содержание железа в ячейке №2
составляло
содержание
металла (как составной части проводящей фазы) менялось весьма значительно.
Например в случае серии №7 для полоски №3 содержание железа в ячейке №2
составляло ![]() , в ячейке №5 –
, в ячейке №5 – ![]() ,
а в ячейке №9 –
,
а в ячейке №9 – ![]() . Подобное соотношение
содержания металла – на середине до
. Подобное соотношение
содержания металла – на середине до ![]() раз больше, чем на
краях, сохранялось и для остальных металлов (
раз больше, чем на
краях, сохранялось и для остальных металлов (![]() ,
, ![]() ) и других номеров ячеек. То есть в любом
случае концентрация проводящей фазы
) и других номеров ячеек. То есть в любом
случае концентрация проводящей фазы ![]() к краям исходной
подложки, то есть по мере изменения
к краям исходной
подложки, то есть по мере изменения ![]() уменьшалась, что однако
это не мешало общему увеличению концентрации
уменьшалась, что однако
это не мешало общему увеличению концентрации ![]() по
мере увеличения
по
мере увеличения ![]() . Так для полоски №2 в той же
серии №7 содержание железа при
. Так для полоски №2 в той же
серии №7 содержание железа при ![]() равнялось
равнялось ![]() , а для полоски №17 при том же значении
, а для полоски №17 при том же значении ![]() составляло
составляло ![]() .
.
7. Соотношение проводимостей на пленках серий №1 и №3
Обратимся теперь к
главной цели настоящей работы – выяснению соотношения динамической и
статической проводимостей, для чего в качестве первого примера обратимся к
пленкам серий №1 и №3, имеющих составы ![]() и
и ![]() соответственно, где превышение
динамической проводимости над статической было отмечено, по-видимому, впервые [31,
32].
соответственно, где превышение
динамической проводимости над статической было отмечено, по-видимому, впервые [31,
32].
Заметим, что серия №2 отличается от серии №1 повышенным содержанием кислорода, несколько ухудшившего как статические, так и динамические свойства пленок (снизившего ту и другую проводимости примерно в полтора раза), по-видимому, из-за снижения проводимости металлической фазы. При этом соотношение проводимостей осталось близким к таковому для серии №1, поэтому подробно на этой серии останавливаться не будем.
Для измерений по сериям
№1 и №3 были выбраны ячейки, лежащие вблизи центра исходной пленки. Толщина
образцов составляла ![]() . В предварительных работах [31,
32], относящихся к подобным составам, было показано, что наиболее объективной
характеристикой соотношения проводимостей является концентрация (процентное
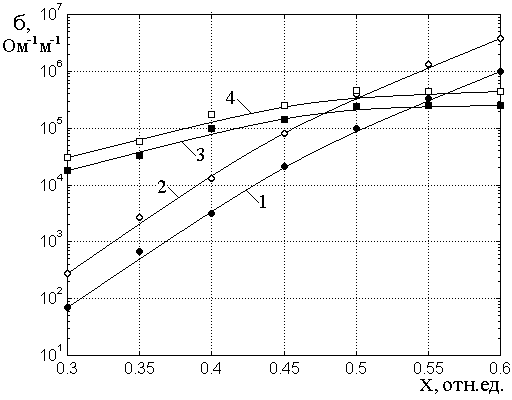
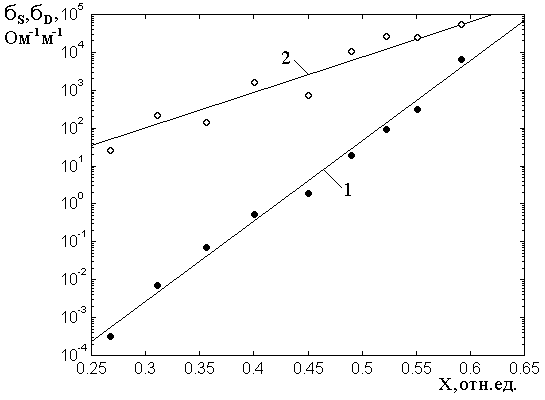
соотношение) проводящей фазы. Обратимся к рис.6, где показаны зависимости
статической (1,3) и динамической (2,4) проводимостей от такой концентрации.
. В предварительных работах [31,
32], относящихся к подобным составам, было показано, что наиболее объективной
характеристикой соотношения проводимостей является концентрация (процентное
соотношение) проводящей фазы. Обратимся к рис.6, где показаны зависимости
статической (1,3) и динамической (2,4) проводимостей от такой концентрации.
Рис.6. Зависимость проводимости от концентрации металлической фазы.
1, 2 – серия №1 (матрица – ![]() ); 3,4 – серия №3 (матрица –
); 3,4 – серия №3 (матрица – ![]() ).
).
Сплошные точки – статическая проводимость, кривые 1, 3.
Открытые точки – динамическая проводимость, кривые 2, 4.
На рис.6 точки – результаты эксперимента, линии построены по эмпирическим формулам, аналогичным приведенным в работах [31, 32].
Кривая 1 построена по формуле:
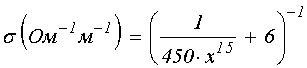 . (8)
. (8)
Кривая 2 построена по формуле:
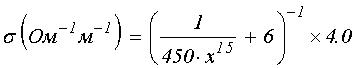 . (9)
. (9)
Кривая 3 построена по формуле:
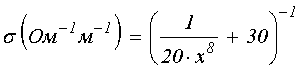 . (10)
. (10)
Кривая 4 построена по формуле:
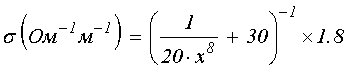 . (11)
. (11)
В этих формулах
переменная ![]() исчисляется в относительных единицах, то
есть в том виде, как она входит в формулу для состава пленки.
исчисляется в относительных единицах, то
есть в том виде, как она входит в формулу для состава пленки.
Из рис.6 можно видеть,
что для пленок обеих серий динамическая проводимость превышает статическую,
причем для серии №1 такое превышение составляет ![]() , а
для серии №3 –
, а
для серии №3 – ![]()
8. Соотношение проводимостей на пленках серии №7
После более или менее уверенного установления превышения динамической проводимости над статической на пленках серий №1 и №3, обратимся к исследованию того же вопроса на пленках других составов.
В качестве
предварительного примера рассмотрим типичные результаты измерения статической и
динамической проводимостей на примере серии №7 (состав ![]() ).
Поскольку разброс значений толщины и проводимости к краям исходной пленки
увеличивался, для измерений были выбраны 16 ячеек, более или менее
рассредоточенные вблизи центральной области исходной пленки, где разброс был
наименьшим. Выбранные для измерений ячейки обведены на рис.5 утолщенными
рамками.
).
Поскольку разброс значений толщины и проводимости к краям исходной пленки
увеличивался, для измерений были выбраны 16 ячеек, более или менее
рассредоточенные вблизи центральной области исходной пленки, где разброс был
наименьшим. Выбранные для измерений ячейки обведены на рис.5 утолщенными
рамками.
Основные результаты сведены в две следующие таблицы.
Таблица №2. Проводимости ячейки S5 для различных полосок ![]() пленок серии №7.
пленок серии №7.
|
N |
d (нм) |
Me (%) |
|
|
|
|
4 |
0.94 |
31.62 |
338 |
56 |
6.04 |
|
6 |
0.94 |
32.44 |
367 |
97 |
3.78 |
|
9 |
1.08 |
36.98 |
712 |
686 |
1.04 |
|
10 |
1.00 |
38.12 |
1061 |
1667 |
0.64 |
|
11 |
0.94 |
39.38 |
2257 |
2800 |
0.81 |
|
13 |
0.94 |
42.43 |
5664 |
3040 |
1.86 |
|
14 |
0.94 |
44.49 |
16870 |
10640 |
1.58 |
|
15 |
0.86 |
45.11 |
24680 |
19380 |
1.27 |
Среднее
арифметическое ![]() :
: ![]()
Среднее квадратичное отклонение: ![]()
Таблица №3. Проводимости ячейки S8 для различных полосок ![]() пленок серии №7.
пленок серии №7.
|
N |
d (нм) |
Me (%) |
|
|
|
|
4 |
0.94 |
31.62 |
338 |
48 |
7.04 |
|
6 |
0.94 |
32.44 |
367 |
24 |
15.3 |
|
9 |
1.08 |
36.98 |
712 |
154 |
4.62 |
|
10 |
1.00 |
38.12 |
1061 |
1000 |
1.06 |
|
11 |
0.94 |
39.38 |
2257 |
3040 |
0.74 |
|
13 |
0.94 |
42.43 |
5664 |
4255 |
1.33 |
|
14 |
0.94 |
44.49 |
16870 |
10640 |
1.58 |
|
15 |
0.86 |
45.11 |
24680 |
16610 |
1.48 |
Среднее
арифметическое ![]() :
: ![]()
Среднее квадратичное отклонение: ![]()
Можно видеть, что в обоих случаях имеются зависимости отношений проводимостей от концентрации металла такого характера, что в пределах исследуемого диапазона концентраций максимумы находятся по краям, а на середину приходится минимум, где соотношение проводимостей в ряде случаев составляют даже меньше единицы (0.64 и 0.74). В обоих случаях минимум обеспечивается пленками с N равным 10 и 11.
Тем не менее, в обоих случаях превышение динамической проводимости над статической по среднему значению имеется.
Следует заметить, что ошибка здесь все же довольно велика. Такое обстоятельство побуждает набрать статистику, то есть просмотреть побольше ячеек, желательно с большим разбросом по всей общей площади исходной пленки.
9. Общий характер пленок серий №7 и №8
Как отмечено во Введении
к настоящей работе, а также подтверждено в разделе №8, более подробное
выяснение природы превышения динамической проводимости над статической требует дополнительных
исследований с учетом разброса данных. В связи с этим обратимся теперь к более
подробному рассмотрению свойств пленок серий №7 и №8, матрица которых содержит
диэлектрическую фазу ![]() .
.
Для упомянутых серий пленок технология выращивания задавалась таким образом, чтобы по длине каждой полоски толщина сохранялась приблизительно постоянной, а по номерам полосок – менялась, при этом самые тонкие полоски получались вблизи краев исходной пленки, а к ее середине их толщина возрастала. Относительно проводящей фазы режим выращивания регулировался таким образом, чтобы с увеличением номера полоски концентрация металла возрастала. При этом по длине полоски концентрация также по мере возможности сохранялась. Таким образом, имелись 18 полосок, технологические параметры роста в пределах каждой из которых сохранялись, но между отдельными полосками различались. То есть можно было ожидать, что внутри каждой полоски параметры ячеек, ей принадлежащих, являлись бы одинаковыми.
Таким образом, технологический режим выращивания пленок обеих серий является одинаковым, поэтому их свойства, в основном, совпадают. Однако некоторые параметры пленок проявляют заметный статистический разброс по отдельным ячейкам, поэтому остановимся сначала на подробном рассмотрении такого разброса на примере пленок серии №7, а затем с учетом характеристик полученного разброса рассмотрим также параметры пленок серии №8.
Ввиду отмеченной в разделе №5 важности технологических параметров, начнем рассмотрение с толщины исследованных пленок, после чего перейдем к концентрации и объему проводящей фазы.
10. Толщина пленок серии №7
В таблице №4 приведены
значения толщины в нм для пленок серии №7 (состав: ![]() ). Геометрия таблицы соответствует исходному
листу пленки, структура разрезания которого на отдельные образцы представлена
на рис.5. Строки таблицы соответствуют номерам полосок
). Геометрия таблицы соответствует исходному
листу пленки, структура разрезания которого на отдельные образцы представлена
на рис.5. Строки таблицы соответствуют номерам полосок ![]() ,
столбцы – номерам ячеек
,
столбцы – номерам ячеек ![]() . Прочерки
соответствуют значениям толщины, лежащим ниже порога чувствительности измерительной
аппаратуры.
. Прочерки
соответствуют значениям толщины, лежащим ниже порога чувствительности измерительной
аппаратуры.
Толщина для каждой ячейки измерялась по 15 точкам на торце образца (раздел №2), после чего полученные значения усреднялись.
Из таблицы можно видеть,
что толщина по площади исходной пленки максимальна вблизи ее середины. Для
последовательности полосок ![]() уменьшение толщины от
середины к краям примерно симметрично и составляет от полутора до двух раз.
уменьшение толщины от
середины к краям примерно симметрично и составляет от полутора до двух раз.
Для последовательности
ячеек ![]() толщина меняется больше, чем для последовательности
полосок. При этом уменьшение толщины проявляется сильнее для ячеек с меньшими
номерами (левые столбцы таблицы), где составляет до 10-12 раз, тогда как для
ячеек с большими номерами (правые столбцы таблицы) составляет всего 3-4 раза.
толщина меняется больше, чем для последовательности
полосок. При этом уменьшение толщины проявляется сильнее для ячеек с меньшими
номерами (левые столбцы таблицы), где составляет до 10-12 раз, тогда как для
ячеек с большими номерами (правые столбцы таблицы) составляет всего 3-4 раза.
Таблица №4. Толщина пленок серии №7.
|
N\S |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
|
01 |
135 |
190 |
400 |
640 |
643 |
636 |
512 |
361 |
274 |
378 |
|
02 |
82 |
168 |
386 |
745 |
850 |
845 |
640 |
444 |
315 |
212 |
|
03 |
98 |
143 |
400 |
925 |
990 |
920 |
760 |
550 |
322 |
229 |
|
04 |
65 |
149 |
446 |
1010 |
1100 |
1150 |
813 |
511 |
378 |
222 |
|
05 |
82 |
147 |
423 |
1120 |
1200 |
1140 |
1220 |
645 |
427 |
231 |
|
06 |
66 |
199 |
430 |
1120 |
1260 |
1085 |
1070 |
737 |
381 |
228 |
|
07 |
84 |
221 |
670 |
980 |
1220 |
1420 |
1310 |
820 |
550 |
310 |
|
08 |
101 |
241 |
805 |
1250 |
1380 |
1595 |
1045 |
755 |
487 |
235 |
|
09 |
165 |
231 |
860 |
1350 |
1490 |
1310 |
955 |
750 |
450 |
292 |
|
10 |
83 |
263 |
848 |
1310 |
1420 |
1370 |
1063 |
765 |
470 |
241 |
|
11 |
91 |
263 |
806 |
1086 |
1395 |
1295 |
1090 |
810 |
552 |
342 |
|
12 |
72 |
187 |
487 |
1145 |
1330 |
1370 |
1070 |
800 |
533 |
323 |
|
13 |
102 |
258 |
878 |
1260 |
1350 |
1330 |
1084 |
795 |
513 |
321 |
|
14 |
95 |
241 |
899 |
1185 |
1380 |
1350 |
1030 |
762 |
487 |
287 |
|
15 |
86 |
242 |
780 |
1080 |
1290 |
1270 |
970 |
710 |
483 |
339 |
|
16 |
85 |
247 |
860 |
1072 |
1190 |
1140 |
960 |
676 |
430 |
311 |
|
17 |
110 |
230 |
751 |
915 |
1123 |
1058 |
918 |
660 |
436 |
316 |
|
18 |
81 |
269 |
531 |
775 |
736 |
850 |
702 |
539 |
364 |
213 |
Перепад толщины между
соседними ячейкам, как правило, не превышает 15%, однако имеются и некоторые
отклонения. Так для ячеек 09/01 и 10/01 толщина составляет ![]() и
и ![]() , то
есть меняется в два раза, однако такие перепады крайне редки и их можно
отнести к случайным флуктуациям технологического режима роста пленок.
, то
есть меняется в два раза, однако такие перепады крайне редки и их можно
отнести к случайным флуктуациям технологического режима роста пленок.
Таким образом, наблюдаемое распределение значений толщины по площади исходной пленки практически полностью соответствует заданному при выращивании пленок технологическому режиму.
Подобные характеристики толщины образцов наблюдались и для остальных серий пленок.
11. Концентрация проводящей фазы в пленках серии №7
В таблице №5 приведены
значения содержания проводящей фазы ![]() , для пленок серии №7,
определенные по составу образцов (раздел №2). Электронно-микроскопический анализ
(раздел №2) давал процентное содержание составляющих пленку элементов. При
этом основу проводящей фазы составляли металлы железо
, для пленок серии №7,
определенные по составу образцов (раздел №2). Электронно-микроскопический анализ
(раздел №2) давал процентное содержание составляющих пленку элементов. При
этом основу проводящей фазы составляли металлы железо ![]() и
кобальт
и
кобальт ![]() , удельные проводимости которых равны
соответственно:
, удельные проводимости которых равны
соответственно: ![]() ,
, ![]() , что
почти на порядок превышает удельную проводимость аморфизатора циркония
, что
почти на порядок превышает удельную проводимость аморфизатора циркония ![]() [51]. Более того, на цирконий в атомном
составе проводящей фазы приходится всего
[51]. Более того, на цирконий в атомном
составе проводящей фазы приходится всего ![]() , тогда
как на железо и кобальт – по
, тогда
как на железо и кобальт – по ![]() , то есть в сумме –
, то есть в сумме – ![]() . Поэтому за основу проводящей фазы по
составу бралась сумма процентных составляющих железа и кобальта, а содержание
циркония, как малая добавка, не учитывалось. Значения рассчитанной таким
образом составляющей проводящей фазы приведены в таблице.
. Поэтому за основу проводящей фазы по
составу бралась сумма процентных составляющих железа и кобальта, а содержание
циркония, как малая добавка, не учитывалось. Значения рассчитанной таким
образом составляющей проводящей фазы приведены в таблице.
Так из таблицы можно
видеть, что концентрация проводящей фазы по мере увеличения номера полоски ![]() возрастает, причем такое возрастание в
абсолютном большинстве рядов ячеек составляет около полутора-двух раз. Только в
ряду ячейки 01 имеет место резкое падение концентрации на первых двух полосках.
Такую аномалию, по-видимому, можно отнести за счет геометрии установки для
напыления пленок (рис.1), так что можно полагать, что на угол пленки,
соответствующий ячейкам 01/02 и особенно 01/01 попадало мало металла из-за его
пространственной удаленности от центра основной подложки.
возрастает, причем такое возрастание в
абсолютном большинстве рядов ячеек составляет около полутора-двух раз. Только в
ряду ячейки 01 имеет место резкое падение концентрации на первых двух полосках.
Такую аномалию, по-видимому, можно отнести за счет геометрии установки для
напыления пленок (рис.1), так что можно полагать, что на угол пленки,
соответствующий ячейкам 01/02 и особенно 01/01 попадало мало металла из-за его
пространственной удаленности от центра основной подложки.
Таблица №5. Концентрация проводящей фазы пленок серии №7.
|
N\S |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
|
01 |
0.28 |
27.3 |
41.8 |
44.5 |
45.6 |
43.8 |
43.7 |
44.5 |
43.3 |
42.1 |
|
02 |
9.60 |
27.4 |
43.7 |
45.6 |
45.0 |
45.3 |
47.6 |
46.1 |
45.4 |
47.2 |
|
03 |
21.7 |
28.5 |
43.5 |
45.3 |
45.3 |
49.1 |
48.8 |
49.5 |
49.5 |
51.9 |
|
04 |
29.3 |
30.6 |
47.8 |
45.5 |
46.7 |
50.6 |
49.6 |
51.2 |
52.1 |
55.7 |
|
05 |
31.2 |
35.2 |
47.2 |
48.0 |
51.4 |
53.9 |
55.4 |
55.3 |
55.8 |
41.9 |
|
06 |
31.2 |
34.7 |
46.6 |
47.2 |
47.0 |
55.6 |
55.0 |
52.4 |
57.2 |
47.5 |
|
07 |
50.8 |
40.7 |
31.6 |
48.6 |
50.5 |
54.6 |
56.1 |
64.8 |
59.7 |
45.6 |
|
08 |
35.9 |
43.3 |
53.5 |
52.4 |
58.1 |
55.8 |
59.4 |
59.4 |
61.6 |
43.5 |
|
09 |
28.6 |
44.5 |
54.7 |
50.4 |
53.7 |
56.4 |
58.1 |
61.5 |
65.5 |
69.1 |
|
10 |
39.0 |
49.0 |
56.2 |
54.7 |
57.8 |
57.5 |
58.6 |
63.3 |
66.4 |
56.1 |
|
11 |
38.5 |
80.0 |
58.1 |
57.5 |
55.2 |
62.0 |
60.9 |
66.3 |
69.1 |
71.4 |
|
12 |
33.6 |
46.5 |
60.1 |
59.6 |
59.5 |
60.7 |
65.9 |
67.2 |
71.9 |
72.5 |
|
13 |
41.1 |
54.4 |
61.6 |
62.9 |
61.8 |
63.1 |
65.9 |
68.6 |
70.8 |
73.3 |
|
14 |
42.8 |
63.2 |
58.8 |
61.9 |
64.6 |
65.7 |
67.6 |
69.6 |
71.4 |
66.7 |
|
15 |
45.9 |
60.7 |
66.7 |
63.8 |
66.6 |
68.0 |
69.3 |
71.7 |
73.6 |
74.9 |
|
16 |
48.6 |
61.7 |
65.5 |
65.8 |
66.6 |
70.8 |
68.8 |
71.8 |
74.2 |
73.0 |
|
17 |
47.0 |
61.2 |
67.8 |
68.7 |
67.4 |
69.4 |
70.4 |
72.1 |
72.8 |
75.0 |
|
18 |
48.1 |
67.2 |
69.2 |
69.3 |
70.4 |
69.9 |
68.8 |
70.0 |
71.2 |
72.0 |
В остальных случаях
отмеченный рост концентрации проводящей фазы с ростом ![]() сохраняется.
сохраняется.
Далее можно видеть, что
по мере увеличения номера ячейки ![]() концентрация
проводящей фазы при прохождении полной длины полоски также увеличивается примерно
в полтора раза. То есть наиболее низкая концентрация проводящей фазы (порядка
концентрация
проводящей фазы при прохождении полной длины полоски также увеличивается примерно
в полтора раза. То есть наиболее низкая концентрация проводящей фазы (порядка ![]() ) имеет место в левом верхнем углу
таблицы, наиболее высокая (порядка
) имеет место в левом верхнем углу
таблицы, наиболее высокая (порядка ![]() ) – в нижнем правом.
) – в нижнем правом.
Дополнительная проверка
по выборочным ячейкам показала, что если провести прямую линию от ячейки 17/01
до ячейки 02/10, то выше этой линии концентрация проводящей фазы составляет
менее ![]() , а ниже – более
, а ниже – более ![]() То
есть такую линию ориентировочно можно считать порогом перколяции пленки,
начиная с которого удельная проводимость должна резко увеличиваться. Это
обстоятельство проверяется далее в разделе №12.
То
есть такую линию ориентировочно можно считать порогом перколяции пленки,
начиная с которого удельная проводимость должна резко увеличиваться. Это
обстоятельство проверяется далее в разделе №12.
12. Относительный объем проводящей фазы в пленках серии №7
Проводящие свойства пленок определяются наличием в их составе проводящей фазы. При этом проводимость тем больше, чем большую относительную часть объема пленки занимает такая фаза.
Рассмотрим теперь
относительный объем суммы составляющих проводящую фазу металлов ![]() ,
, ![]() ,
, ![]() для пленок серии №7 ( состав:
для пленок серии №7 ( состав: ![]() ).
).
Объем металлической и диэлектрической фаз будем вычислять как сумму объемов составляющих каждую фазу атомов, где каждый атом положим в виде сферы с радиусом [51]:
для железа: ![]() ;
;
для кобальта: ![]() ;
;
для циркония: ![]() ;
;
для кальция: ![]() ;
;
для фтора: ![]() .
.
При этом относительный
объем проводящей фазы ![]() находим по формуле:
находим по формуле:
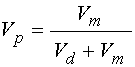 , (12)
, (12)
где ![]() –
объем проводящей (металлической) фазы,
–
объем проводящей (металлической) фазы, ![]() –
объем диэлектрической фазы.
–
объем диэлектрической фазы.
Для вычисления объемов в качестве параметров будем использовать значения концентрации соответствующих компонент состава пленки, определенных по методике, описанной в разделе №2.
Значения концентрации для суммы металлов железа и кобальта приведены в таблице №5 (раздел №11). При вычислении объема по формуле (12) концентрации надо брать по каждому элементу в отдельности. Эти концентрации здесь не приведены вследствие громоздкости таблиц, а также аналогичности их характера концентрациям, приведенным в таблице №5.
Таким образом, объем диэлектрической фазы в рамках одной структурной единицы состава будем вычислять по формуле:
![]() ,
(13)
,
(13)
а объем металлической фазы, вычисляем по формуле:
![]() .
(14)
.
(14)
Полученные по формуле (12)
с учетом (13)-(14) значения относительного объема проводящей фазы ![]() приведены в таблице №6.
приведены в таблице №6.
Можно видеть, что характер этой таблицы, в основном, подобен характеру таблицы для концентрации проводящей фазы (№5). Так относительный объем проводящей фазы увеличивается по двум направлениям: по мере увеличения номера полоски, а в пределах каждой полоски – по мере увеличения номера ячейки. В первом из этих случаев (по столбцам таблицы) объем увеличивается от полутора до двух раз, кроме ячеек 01, где такое увеличение составляет около пяти. Во втором случае (по строкам таблицы) объем увеличивается несколько меньше полутора раз. Аномальное поведение ячеек в левом верхнем углу таблицы объясняется теми же причинами, что и подобная аномалия в таблице №5.
Таблица №6. Относительный объем проводящей фазы пленок серии №7.
|
N/S |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
|
01 |
0.133 |
0.401 |
0.444 |
0.412 |
0.414 |
0.413 |
0.440 |
0.471 |
0.504 |
0.535 |
|
02 |
0.317 |
0.398 |
0.448 |
0.404 |
0.403 |
0.405 |
0.443 |
0.489 |
0.532 |
0.592 |
|
03 |
0.451 |
0.408 |
0.451 |
0.397 |
0.393 |
0.406 |
0.446 |
0.489 |
0.566 |
0.612 |
|
04 |
0.476 |
0.426 |
0.456 |
0.389 |
0.389 |
0.404 |
0.446 |
0.506 |
0.578 |
0.654 |
|
05 |
0.515 |
0.450 |
0.459 |
0.401 |
0.397 |
0.461 |
0.533 |
0.624 |
0.550 |
- |
|
06 |
0.514 |
0.470 |
0.484 |
0.401 |
0.397 |
0.417 |
0.455 |
0.516 |
0.614 |
0.576 |
|
07 |
0.494 |
0.490 |
0.533 |
0.432 |
0.431 |
0.458 |
0.505 |
0.582 |
0.673 |
0.776 |
|
08 |
0.562 |
0.520 |
0.488 |
0.457 |
0.480 |
0.521 |
0.602 |
0.690 |
0.582 |
- |
|
09 |
0.727 |
0.525 |
0.516 |
0.476 |
0.484 |
0.509 |
0.565 |
0.642 |
0.739 |
0.827 |
|
10 |
0.571 |
0.554 |
0.528 |
0.502 |
0.510 |
0.531 |
0.589 |
0.657 |
0.752 |
0.670 |
|
11 |
0.581 |
0.509 |
0.560 |
0.529 |
0.529 |
0.561 |
0.619 |
0.699 |
0.789 |
0.859 |
|
12 |
0.585 |
0.583 |
0.639 |
0.564 |
0.560 |
0.597 |
0.652 |
0.716 |
0.805 |
0.866 |
|
13 |
0.609 |
0.620 |
0.607 |
0.590 |
0.595 |
0.623 |
0.677 |
0.744 |
0.820 |
0.876 |
|
14 |
0.623 |
0.625 |
0.664 |
0.618 |
0.618 |
0.652 |
0.698 |
0.762 |
0.831 |
0.344 |
|
15 |
0.629 |
0.674 |
0.649 |
0.636 |
0.649 |
0.679 |
0.728 |
0.788 |
0.852 |
0.908 |
|
16 |
0.656 |
0.686 |
0.659 |
0.661 |
0.663 |
0.701 |
0.736 |
0.793 |
0.859 |
0.899 |
|
17 |
0.657 |
0.704 |
0.682 |
0.678 |
0.680 |
0.720 |
0.759 |
0.808 |
0.864 |
0.896 |
|
18 |
0.687 |
0.746 |
0.719 |
0.718 |
0.726 |
0.741 |
0.763 |
0.796 |
0.837 |
0.861 |
Более подробное
рассмотрение показывает, что объем проводящей фазы более ![]() приходится ниже прямой, проходящей от
ячейки 06/01 к ячейке 01/09. Аналогично разделу №11, такую линию также можно
считать порогом перколяции пленки, начиная с которого удельная проводимость
должна резко увеличиваться. Это обстоятельство проверяется далее в разделе №13.
приходится ниже прямой, проходящей от
ячейки 06/01 к ячейке 01/09. Аналогично разделу №11, такую линию также можно
считать порогом перколяции пленки, начиная с которого удельная проводимость
должна резко увеличиваться. Это обстоятельство проверяется далее в разделе №13.
13. Статическая удельная проводимость пленок серии №7
Обратимся теперь к рассмотрению электрических свойств пленок, из которых остановимся сначала на статической проводимости.
В таблице №7 приведены
значения удельной проводимости, измеренные на постоянном токе, для пленок серии
№7 (состав: ![]() ).
).
Геометрия таблицы
соответствует исходному листу пленки, структура разрезания которого на
отдельные образцы представлена на рис.5. Строки таблицы соответствуют номерам
полосок ![]() , столбцы – номерам ячеек
, столбцы – номерам ячеек ![]() .
.
Для удобства изображения
в едином масштабе, представленные в таблице величины проводимости занижены в ![]() раз, то есть для получения истинной
проводимости в единицах
раз, то есть для получения истинной
проводимости в единицах ![]() надо приведенные в
таблице значения умножать на
надо приведенные в
таблице значения умножать на ![]() . Прочерки
соответствуют значениям проводимости, лежащим ниже порога чувствительности
измерительной аппаратуры.
. Прочерки
соответствуют значениям проводимости, лежащим ниже порога чувствительности
измерительной аппаратуры.
Проводимость в каждой ячейке измерялась на нескольких (до пяти) локальных участках образца, после чего полученные значения усреднялись.
Из таблицы можно видеть, что локальная проводимость по площади исходной пленки претерпевает сильные изменения. Наибольшая неоднородность пленки проявляется вблизи ее краев, особенно края, соответствующего большей толщине, то есть для полосок 15-18. Так для ячейки 17/01 приведенное в таблице значение составляет 1136.0, тогда как для соседних ячеек 17/02, 18/01, 18/02 падает до 109.0, 61.7, 33.8 соответственно.
В центральной части пленки неоднородность проявляется меньше, однако и там есть отдельные выбросы, например для ячеек 12/2, 11/6 и некоторых других, где проводимость при переходе к соседним ячейкам меняется в 2-3 раза.
Можно полагать, наблюдаемый в некоторых случаях столь сильный разброс значений проводимости обусловлен стохастическим характером условий перколяции в гранулированной структуре пленок.
Таблица №7. Статическая удельная проводимость пленок серии №7.
|
N\S |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
|
01 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
02 |
0.16 |
0.24 |
0.14 |
0.06 |
0.06 |
0.04 |
0.01 |
0.26 |
- |
- |
|
03 |
0.23 |
0.54 |
0.28 |
0.09 |
0.06 |
0.09 |
0.07 |
0.09 |
- |
- |
|
04 |
2.20 |
1.34 |
0.45 |
0.12 |
0.05 |
0.02 |
0.12 |
0.09 |
- |
- |
|
05 |
4.88 |
1.36 |
0.53 |
0.11 |
0.03 |
0.02 |
0.01 |
0.06 |
0.01 |
- |
|
06 |
11.6 |
4.19 |
1.16 |
0.39 |
0.07 |
0.09 |
0.04 |
0.03 |
- |
- |
|
07 |
24.8 |
6.46 |
1.48 |
0.36 |
0.14 |
0.06 |
0.02 |
0.01 |
- |
- |
|
08 |
66.0 |
27.7 |
6.21 |
1.14 |
0.38 |
0.26 |
0.02 |
0.04 |
0.01 |
- |
|
09 |
33.7 |
33.3 |
7.75 |
1.29 |
0.49 |
0.22 |
0.03 |
0.22 |
0.26 |
- |
|
10 |
241.0 |
126.0 |
16.8 |
1.91 |
1.17 |
0.40 |
0.02 |
1.31 |
0.71 |
- |
|
11 |
199.0 |
95.1 |
35.4 |
3.68 |
1.89 |
2.21 |
0.30 |
3.53 |
1.29 |
- |
|
12 |
231.0 |
267.0 |
68.4 |
25.7 |
1.67 |
0.49 |
0.05 |
0.10 |
0.85 |
- |
|
13 |
17.8 |
55.4 |
11.4 |
31.7 |
2.12 |
0.50 |
0.26 |
5.03 |
0.35 |
- |
|
14 |
11.7 |
296.0 |
8.56 |
24.1 |
7.25 |
2.47 |
1.94 |
13.1 |
22.9 |
0.07 |
|
15 |
646.0 |
318.0 |
36.6 |
19.3 |
12.9 |
3.58 |
2.94 |
20.1 |
9.00 |
- |
|
16 |
904.0 |
405.0 |
68.4 |
71.8 |
120.0 |
86.8 |
8.70 |
38.76 |
18.9 |
- |
|
17 |
1136.0 |
109.0 |
22.2 |
15.6 |
2.23 |
6.30 |
2.59 |
18.9 |
12.7 |
- |
|
18 |
61.7 |
33.8 |
40.1 |
41.6 |
37.7 |
4.70 |
10.9 |
30.9 |
0.55 |
- |
В качестве общих тенденций можно отметить, что проводимость при увеличении номера полоски возрастает на 2-3 порядка, а при увеличении номера ячейки падает также примерно на 2-3 порядка.
Представляет интерес сопоставить характер распределения удельной проводимости по площади исходной пленки с распределением толщины и металлической фазы по этой площади.
Так из сравнения с
таблицей №5 можно видеть, что условие реализации перколяции, когда концентрация
металлической фазы превышает ![]() , более или менее
выполняется только для ячеек не выше 05-06. При больших же номерах ячеек
проводимость падает, несмотря на увеличение концентрации проводящей фазы. Из
сравнения с таблицей №4 можно видеть, что такое изменение характера проводящей
фазы при увеличении номера ячейки коррелирует с изменением толщины в этом же
диапазоне номеров ячеек.
, более или менее
выполняется только для ячеек не выше 05-06. При больших же номерах ячеек
проводимость падает, несмотря на увеличение концентрации проводящей фазы. Из
сравнения с таблицей №4 можно видеть, что такое изменение характера проводящей
фазы при увеличении номера ячейки коррелирует с изменением толщины в этом же
диапазоне номеров ячеек.
С другой стороны, как
установлено в работе [34], имеется критическое значение толщины, ниже которого
статическая проводимость пленки падает. Это критическое значение определяется
размером кластеров, формирующих зернистый характер пленок, и составляет около ![]() . При толщине меньшей этой величины
кластер уже «не помещается» между противоположными поверхностями пленки, в
результате чего вместо сферического он приобретает сплюснутый характер. При
этом за счет чисто геометрического эффекта его абсолютная проводимость
уменьшается, приводя, в результате совокупной деятельности множества кластеров,
к уменьшению удельной проводимости пленки в целом.
. При толщине меньшей этой величины
кластер уже «не помещается» между противоположными поверхностями пленки, в
результате чего вместо сферического он приобретает сплюснутый характер. При
этом за счет чисто геометрического эффекта его абсолютная проводимость
уменьшается, приводя, в результате совокупной деятельности множества кластеров,
к уменьшению удельной проводимости пленки в целом.
Из таблицы №4 можно видеть, что толщина пленок спадает, начиная с ячеек 07-08, а на ячейках 09-10 становится ниже критического значения. Таким образом, можно полагать, что отмеченное падение удельной проводимости для ячеек с номерами выше 06-07 обусловлено именно падением их толщины ниже критического значения.
В разделах №11 и №12 отмечено,
что по таблицам №5 и №6 можно отметить граничные линии, соответствующие
концентрации равной ![]() (таблица №5) и объема
проводящей фазы (таблица №6), равной тому же значению. Можно полагать, что выше
этих линий условия для перколяции отсутствуют, тогда как ниже – имеют место.
Так для концентрации такая линия проходит между ячейками 17/01 и 02/10, а для
объема – между ячейками 06/01 и 01/09, то есть, хотя наклон обеих линий
положителен, но первая линия располагается несколько ниже второй.
(таблица №5) и объема
проводящей фазы (таблица №6), равной тому же значению. Можно полагать, что выше
этих линий условия для перколяции отсутствуют, тогда как ниже – имеют место.
Так для концентрации такая линия проходит между ячейками 17/01 и 02/10, а для
объема – между ячейками 06/01 и 01/09, то есть, хотя наклон обеих линий
положителен, но первая линия располагается несколько ниже второй.
Сильный разброс значений
проводимости в таблице №7 не позволяет сделать однозначного вывода о том, какой
параметр больше соответствует порогу перколяции – концентрация проводящей фазы,
равная ![]() (таблица №5) или относительный ее объем,
равный также
(таблица №5) или относительный ее объем,
равный также ![]() (таблица №6). Однако из таблицы
№7 все же можно сделать вывод, что перколяция, проявляющаяся в скачке
проводимости, происходит, в основном, вблизи середины между этими двумя прямыми,
скорее всего, ближе к верхней прямой, то есть около
(таблица №6). Однако из таблицы
№7 все же можно сделать вывод, что перколяция, проявляющаяся в скачке
проводимости, происходит, в основном, вблизи середины между этими двумя прямыми,
скорее всего, ближе к верхней прямой, то есть около ![]() (или,
что то же самое,
(или,
что то же самое, ![]() ). Заметим, что в условиях довольно
высокого разброса данных по соседним ячейкам, более точное установление этого
значения, по-видимому, возможно только при статистической обработке
значительного количества материала, превосходящего рамки настоящей работы.
). Заметим, что в условиях довольно
высокого разброса данных по соседним ячейкам, более точное установление этого
значения, по-видимому, возможно только при статистической обработке
значительного количества материала, превосходящего рамки настоящей работы.
14. Основные характеристики пленок серии №8
В материалах, описанных в
предыдущих разделах, был выявлен сильный разброс параметров по соседствующим
или достаточно близко расположенным ячейкам на примере пленок серии №7.
Рассмотрим теперь характер разброса данных более подробно на примере пленок серии
№8 (состав ![]() ). С технологической стороны эта серия
повторяет серию №7, поэтому многие результаты по этим сериям можно считать общими.
Некоторые предварительные данные по пленкам серии №8 приведены в работе [41].
). С технологической стороны эта серия
повторяет серию №7, поэтому многие результаты по этим сериям можно считать общими.
Некоторые предварительные данные по пленкам серии №8 приведены в работе [41].
15. Толщина и концентрация проводящей фазы пленок серии №8
Контрольные измерения
показали, что толщина пленки в пределах одной полоски по разным ячейкам
меняется не более чем на ![]() . Поэтому, учитывая
высокую трудоемкость измерения толщины, она была измерена с максимальной
возможной точностью только на ячейках №5, принадлежащих всем полоскам (то есть
вблизи середины каждой полоски). В расчетах проводимости предполагалось, что
значения толщины на всех остальных ячейках той же полоски являются теми же самыми.
. Поэтому, учитывая
высокую трудоемкость измерения толщины, она была измерена с максимальной
возможной точностью только на ячейках №5, принадлежащих всем полоскам (то есть
вблизи середины каждой полоски). В расчетах проводимости предполагалось, что
значения толщины на всех остальных ячейках той же полоски являются теми же самыми.
Полученные значения толщины иллюстрируются рис.7. По горизонтальной оси отложены номера полосок, по вертикальной – измеренные значения толщины. Точки – результаты эксперимента, сплошная линия – эмпирическое приближение, построенное по формуле:
![]() , (15)
, (15)
где ![]() –
номер полоски.
–
номер полоски.
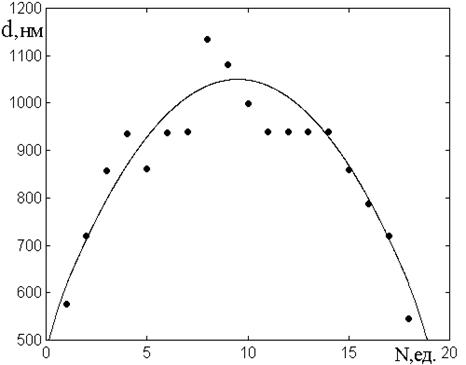
Рис.7. Толщина пленок по ячейкам №5 при различных номерах полосок (серия №8).
Можно видеть, что
значения толщины подчиняются закону квадратичной параболы с точностью не хуже ![]() , причем к краям исходной пленки, где
толщина меньше, эта точность несколько возрастает (до
, причем к краям исходной пленки, где
толщина меньше, эта точность несколько возрастает (до ![]() ).
).
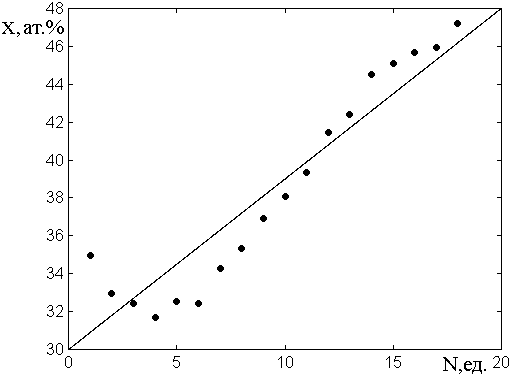
На рис.8 показана зависимость концентрации металла от номера полоски, измеренная по тем же ячейкам №5. По горизонтальной оси отложены номера полосок, по вертикальной – значения концентрации. Точки – результаты эксперимента, сплошная линия – эмпирическое приближение, построенное по формуле:
![]() , (16)
, (16)
где ![]() –
номер полоски.
–
номер полоски.
Рис.8. Концентрация проводящей фазы по ячейкам №5 при различных номерах полосок (серия №8).
Можно видеть, что
значения концентрации подчиняются линейному закону с точностью не хуже ![]() вблизи
вблизи ![]() , а при
больших значениях
, а при
больших значениях ![]() точность возрастает до
точность возрастает до ![]() .
.
Следует заметить, что в
пределах от ![]() до
до ![]() значения
концентрации довольно близко (с точностью до
значения
концентрации довольно близко (с точностью до ![]() )
ложатся на более крутую прямую линию с угловым коэффициентом порядка
)
ложатся на более крутую прямую линию с угловым коэффициентом порядка ![]() . Однако вне такого интервала ниже
. Однако вне такого интервала ниже ![]() зависимость резко идет вверх, а выше
зависимость резко идет вверх, а выше ![]() рост ее замедляется настолько, что
угловой коэффициент падает до
рост ее замедляется настолько, что
угловой коэффициент падает до ![]() . Можно полагать, что
такие отклонения вблизи краев исходной пленки связаны с вариациями режима
роста, трудно контролируемыми при весьма большой ее площади. Тем не менее,
видно, что на преобладающей центральной области пленки от
. Можно полагать, что
такие отклонения вблизи краев исходной пленки связаны с вариациями режима
роста, трудно контролируемыми при весьма большой ее площади. Тем не менее,
видно, что на преобладающей центральной области пленки от ![]() до
до ![]() линейный
рост концентрации с увеличением номера полоски выполняется с точностью не хуже
линейный
рост концентрации с увеличением номера полоски выполняется с точностью не хуже ![]() .
.
16. Общий характер разброса данных по статической и динамической проводимости пленок серии №8
Измерение статической проводимости по постоянному току проводилось по каждой ячейке каждой отдельной полоски исходной пленки (серия №8). Следует отметить, что контрольные измерения, несмотря на сходство технологических параметров в пределах одной полоски, выявили значительный разброс данных по отдельным ячейкам.
В качестве иллюстрации возьмем две полоски, близкие к краям исходной пленки, и одну, близкую к середине. Ячейки на каждой полоске также выберем две по краям и одну посередине.
Так при ![]() проводимости для ячеек 2, 5, 8 равны
соответственно:
проводимости для ячеек 2, 5, 8 равны
соответственно: ![]() ,
, ![]() ,
, ![]() , откуда получаем среднее арифметическое
со средней квадратичной ошибкой:
, откуда получаем среднее арифметическое
со средней квадратичной ошибкой: ![]() . При
. При ![]() проводимость равна:
проводимость равна: ![]() , то есть здесь ошибка уже превышает саму
измеряемую величину. При
, то есть здесь ошибка уже превышает саму
измеряемую величину. При ![]() проводимость равна:
проводимость равна: ![]() , то есть здесь ошибка также приближается
к измеряемой величине. Подобная картина наблюдается и по другим полоскам.
, то есть здесь ошибка также приближается
к измеряемой величине. Подобная картина наблюдается и по другим полоскам.
Столь высокий разброс
данных, по-видимому, обусловлен крайне сложным морфологическим характером
пленок. Так в работах [7], а также [29,
30, 46, 50] показано, что размер гранул
может меняться до десятков нанометров, гранулы могут объединяться в более
крупные кластеры, в том числе столбчатого характера, а в некоторых случае на
пленках могут образовываться поры размером до сотен нанометров, то есть
сравнимые с толщиной самой пленки. Столь неоднородный характер пленок
проявляется тем заметнее, чем меньшая область выделяется для исследования.
Таким образом, можно полагать, что размер рабочей области между контактами
порядка ![]() недостаточен для интегральной оценки
проводимости на длине не только полоски, но даже одной ячейки.
недостаточен для интегральной оценки
проводимости на длине не только полоски, но даже одной ячейки.
Такое обстоятельство, для получения более или менее достоверных результатов, вынуждает идти по пути усреднения параметров для каждой полоски по всем ее ячейкам. Проверка показывает, что при таком усреднении квадратичная ошибка, как правило, не превышает половины измеряемой величины.
Измерение динамической проводимости по коэффициенту отражения СВЧ сигнала также проводилось для каждой ячейки каждой отдельной полоски исходной пленки (серия №8).
Измерения проводились в
диапазоне частот от ![]() до
до ![]() , причем
какой-либо заметной зависимости от частоты обнаружено не было. На всех частотах
при
, причем
какой-либо заметной зависимости от частоты обнаружено не было. На всех частотах
при ![]() (то есть при концентрации металлической
фазы
(то есть при концентрации металлической
фазы ![]() менее
менее ![]() )
коэффициент отражения по мощности
)
коэффициент отражения по мощности ![]() не превышал
не превышал ![]() . При увеличении
. При увеличении ![]() вплоть
до
вплоть
до ![]() (то есть
(то есть ![]() до
до ![]() ) коэффициент
) коэффициент ![]() плавно
возрастал, составляя при
плавно
возрастал, составляя при ![]() величину
величину ![]() . Такая зависимость
. Такая зависимость ![]() от концентрации металла была аналогична
наблюдавшейся в работах [29-32, 36,
37] и отражала увеличение динамической
проводимости
от концентрации металла была аналогична
наблюдавшейся в работах [29-32, 36,
37] и отражала увеличение динамической
проводимости ![]() по мере роста
по мере роста ![]() ,
причем порогу перколяции соответствовала величина порядка
,
причем порогу перколяции соответствовала величина порядка ![]() .
.
Контрольные измерения, выполненные по всем ячейкам каждой отдельной полоски, показали значительно меньший разброс данных, чем для статической проводимости: в пределах одного порядка при общей величине в пять-шесть порядков, то есть подобный наблюдавшемуся в работе [37].
Можно полагать, что такое обстоятельство свидетельствует в пользу меньшей чувствительности измерения проводимости на СВЧ, чем на постоянном токе, к дефектам пленки, по-видимому, из-за большей интегрированности СВЧ волноводного метода, захватывающего одновременно значительно большую (до 10 раз) площадь пленки, чем при измерении в статике.
17. Сравнение статической и динамической проводимостей пленок серии №8
Рассмотрим теперь сравнительные значения статической и динамической проводимостей пленок серии №8, для чего обратимся к рис.9.
На этом рисунке значения статической проводимости показаны сплошными точками. Аппроксимирующая эмпирическая кривая (1) построена по формуле:
![]() , (17)
, (17)
где ![]() –
номер полоски.
–
номер полоски.
Рис.9. Зависимости статической
(кривая 1, сплошные точки) и
динамической (кривая 2, открытые точки)
проводимостей от номера полоски (серия №8).
Можно видеть, что
зависимость ![]() в логарифмическом масштабе довольно
близка к линейной на всем протяжении исходной пленки по большему размеру.
в логарифмическом масштабе довольно
близка к линейной на всем протяжении исходной пленки по большему размеру.
На том же рис.9 открытыми точками показана зависимость динамической проводимости от номера полоски. Аппроксимирующая эмпирическая кривая 2 построена по формуле:
![]() , (18)
, (18)
где ![]() –
номер полоски.
–
номер полоски.
Можно видеть, что
зависимость ![]() в логарифмическом масштабе при
в логарифмическом масштабе при ![]() близка к линейной и практически совпадает
с аналогичной кривой 1 для статической проводимости. Однако при
близка к линейной и практически совпадает
с аналогичной кривой 1 для статической проводимости. Однако при ![]() кривая 2 отклоняется от кривой 1 вверх
тем сильнее, чем
кривая 2 отклоняется от кривой 1 вверх
тем сильнее, чем ![]() меньше, по сути дела при
меньше, по сути дела при ![]() выходя на горизонтальный участок (при
выходя на горизонтальный участок (при ![]() ). То есть в этой области динамическая
проводимость превышает статическую тем сильнее, чем номер полоски
). То есть в этой области динамическая
проводимость превышает статическую тем сильнее, чем номер полоски ![]() меньше.
меньше.
Еще более наглядную иллюстрацию превышения динамической проводимости над статической дает рис.10, где точками показана построенная по данным рис.9 зависимость отношения динамической и статической проводимостей от номера полоски. Аппроксимирующая эмпирическая кривая построена по формуле:
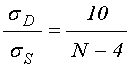 , (19)
, (19)
где ![]() –
номер полоски.
–
номер полоски.
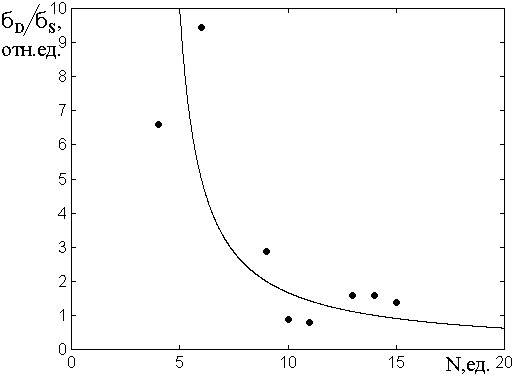
Рис.10. Зависимость отношения динамической и статической проводимостей от номера полоски (серия №8).
Можно видеть, что хотя
разброс точек довольно велик и достигает ![]() , тем
не менее превышение динамической проводимости над статической проявляется
совершенно ярко и при
, тем
не менее превышение динамической проводимости над статической проявляется
совершенно ярко и при ![]() достигает почти порядка (точнее
– около 7-9 раз).
достигает почти порядка (точнее
– около 7-9 раз).
18. Некоторые дополнительные наблюдения
Рассмотрим полученные результаты более подробно с физической стороны, в том числе с учетом результатов предшествующих работ.
Во-первых отметим, что,
согласно рис.8, номер полоски ![]() , где кривая 2 на рис.9
заметно отходит от кривой 1, соответствует концентрации металлической фазы
около
, где кривая 2 на рис.9
заметно отходит от кривой 1, соответствует концентрации металлической фазы
около ![]() , что весьма близко к значению
, что весьма близко к значению ![]() , где коэффициент отражения возрастает
благодаря перколяции (раздел №2).
, где коэффициент отражения возрастает
благодаря перколяции (раздел №2).
С другой стороны,
согласно рис.7, толщина пленки по обе стороны от значения ![]() уменьшается симметричным образом. Однако
из рис.9 и рис.10 видно, что соотношение между динамической и статической
проводимостями возрастает только по одну сторону от этой точки, то есть только
при
уменьшается симметричным образом. Однако
из рис.9 и рис.10 видно, что соотношение между динамической и статической
проводимостями возрастает только по одну сторону от этой точки, то есть только
при ![]() или при концентрации металлической фазы
менее значения
или при концентрации металлической фазы
менее значения ![]() , соответствующего перколяции.
, соответствующего перколяции.
Таким образом, можно сделать вывод, что превышение динамической проводимости над статической имеет место только тогда, когда пленка представляет собой набор еще разделенных определенными промежутками проводящих гранул, то есть в формировании динамической проводимости имеет место механизм внутригранулярных токов [35], микроскопическая картина которого рассмотрена в работе [34].
Далее можно отметить, что
в работе [35] наблюдалось столь значительное превышение динамической
проводимости над статической, как на два-три порядка, только в области толщин
пленок не более нескольких десятков нанометров. Так из рис.4 в этой работе
можно видеть, что при толщине порядка ![]() превышение
составляет не более
превышение
составляет не более ![]() раз, при толщине
раз, при толщине ![]() возрастает примерно до
возрастает примерно до ![]() и только при толщине
и только при толщине ![]() достигает
достигает ![]() .
.
То есть в исследуемом в
настоящей работе диапазоне толщин от ![]() до
до ![]() превышение не может составлять более
одного десятка. Таким образом, наблюдаемое здесь на рис.4 превышение в 7-9 раз
близко к таковому, наблюдавшемуся в работе [35] в том же диапазоне толщин.
превышение не может составлять более
одного десятка. Таким образом, наблюдаемое здесь на рис.4 превышение в 7-9 раз
близко к таковому, наблюдавшемуся в работе [35] в том же диапазоне толщин.
Следует заметить, что
впервые описанное в работах [30, 31] подобное превышение, составлявшее там не
более четырех раз, своей сравнительной малостью, по-видимому, обязано
опять-таки слишком большой толщине исследованных там пленок – ![]() .
.
Итак, можно полагать, что
необходимыми условиями для значительного превышения динамической проводимости
над статической (не менее одного порядка) является наличие в пленке
несмыкающихся металлических гранул, не достигающих порога перколяции, а также
достаточно малая толщина пленки – ниже критического значения порядка ![]() .
.
19. Соотношение проводимостей в пленках серии №6
В разделе №18 отмечено,
что в качестве одного из условий значительного превышения динамической
проводимости над статической может выступать малая толщина пленок. Здесь под
«малой» следует подразумевать толщину, значительно меньшую критической,
сравнимой с размерами кластеров, которая близка к ![]() .
Однако исследованные в разделе №18 пленки серии №8 имеют толщину, как правило,
близкую или заметно большую критической величины. Поэтому представляет интерес
рассмотреть пленки, толщины которых лежат значительно ниже критического
значения. С такой целью была выбрана серия №6, имеющая тот же состав, что и
серия №8 –
.
Однако исследованные в разделе №18 пленки серии №8 имеют толщину, как правило,
близкую или заметно большую критической величины. Поэтому представляет интерес
рассмотреть пленки, толщины которых лежат значительно ниже критического
значения. С такой целью была выбрана серия №6, имеющая тот же состав, что и
серия №8 – ![]() , но толщину в пределах
, но толщину в пределах ![]() .
.
Полученные в результате измерений параметры пленок серии №6 приведены в таблице №8.
Таблица №8. Параметры пленок серии №6.
|
|
|
|
|
|
|
16/02 |
247 |
0.25 |
62 |
0.68 |
|
17/02 |
230 |
2.75 |
61 |
0.70 |
|
05/02 |
147 |
0.21 |
32 |
0.67 |
|
17/01 |
110 |
0.26 |
47 |
0.55 |
|
03/01 |
98 |
1.29 |
22 |
0.45 |
|
16/01 |
85 |
0.05 |
48 |
0.68 |
В первом столбце таблицы приведены номера ячеек, в которых производились измерения. Пленки расположены в порядке убывания толщины, которая приведена во втором столбце таблицы. В третьем столбце приведено отношение динамической проводимости к статической, измеренное в относительных единицах. В следующих двух столбцах приведено процентное содержание металлической фазы и ее относительный объем.
Из таблицы можно видеть,
что при уменьшении толщины никакой из параметров, приведенных в остальных
столбцах таблицы, монотонно не меняется. Все параметры испытывают определенные
скачки в ту или другую сторон, так что безусловного вывода о влиянии толщины
сделать нельзя. Так отношение проводимостей меняется от ![]() до
до
![]() со средним значением
со средним значением ![]() То есть, в среднем, при малых толщинах
динамическая проводимость перестает преобладать над статической и даже в ряде
случаев может быть меньше нее.
То есть, в среднем, при малых толщинах
динамическая проводимость перестает преобладать над статической и даже в ряде
случаев может быть меньше нее.
Заметим, что следующее из
рис.9 и 10 преобладание динамической проводимости над статической в ![]() раз, противоречием к наблюдаемому здесь
отсутствию такового не является, так как упомянутые рисунки относятся к полоскам
№5 – №7, где, согласно рис.7 толщина составляет
раз, противоречием к наблюдаемому здесь
отсутствию такового не является, так как упомянутые рисунки относятся к полоскам
№5 – №7, где, согласно рис.7 толщина составляет ![]() , что
значительно превышает критическую величину
, что
значительно превышает критическую величину ![]() , то
есть эти рисунки относятся к другим условиям.
, то
есть эти рисунки относятся к другим условиям.
Наблюдаемое здесь уменьшение динамической проводимости при уменьшении толщины пленки можно объяснить тем, что, согласно модели гранулярных токов [37], при малой толщине происходит взаимная компенсация магнитных полей, исходящих от противоположных поверхностей пленки, в результате чего отражение СВЧ сигнала от пленки уменьшается.
Таким образом, при уменьшении толщины пленки, несмотря на сохранение проводимости металлической фазы, коэффициент отражения СВЧ сигнала от пленки падает, приводя к уменьшению определяемого по этому коэффициенту значения динамической проводимости.
Заметим, что, вообще говоря, коэффициент отражения при уменьшении толщины должен уменьшаться в любом случае просто за счет малости взаимодействия СВЧ сигнала с пленкой, то есть, чем тоньше пленка, тем меньше должно быть отражение. Здесь однако такое уменьшение за счет компенсации полей от противоположных поверхностей пленки дополнительно усиливается.
Модель гранулярных токов для определения коэффициента отражения дает при этом следующую формулу:
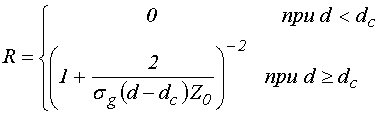 , (20)
, (20)
где ![]() –
критическое значение толщины, которое можно положить равным
–
критическое значение толщины, которое можно положить равным ![]() . В этой формуле вторая часть совпадает с
приведенной в работе [37], а первая просто положена равной нулю. При этом
проводимость
. В этой формуле вторая часть совпадает с
приведенной в работе [37], а первая просто положена равной нулю. При этом
проводимость ![]() от толщины
от толщины ![]() никак не зависит, а определяется только
параметрами материала гранулы. При использовании этой формулы начало отсчета
толщины надо брать от критического значения.
никак не зависит, а определяется только
параметрами материала гранулы. При использовании этой формулы начало отсчета
толщины надо брать от критического значения.
20. Соотношение проводимостей в пленках серии №5
Рассмотрим теперь
соотношение статической и динамической проводимостей на пленках серии №5
(состав ![]() ). Пленки подобного состава
рассматривались в работах [34-36], причем было обнаружено превышение
динамической проводимости над статической на величину более двух порядков.
Аналогичные результаты для пленок серии №4 приведены здесь разделе №5, как
иллюстрация к методике измерения динамической проводимости. Так на
рис.3
приведены зависимости коэффициента отражения (кривая 1), а на рис.4 приведены
зависимости статической (1) и динамической (2) проводимостей от толщины пленки.
Можно видеть, что превышение динамической проводимости над статической при
малых толщинах достигает двух порядков. Однако приведенные на рис.4 данные не
дают возможности однозначно выяснить причину столь большого превышения, так как
в формировании приведенных там зависимостей одновременно участвуют два фактора
– состав диэлектрической матрицы
). Пленки подобного состава
рассматривались в работах [34-36], причем было обнаружено превышение
динамической проводимости над статической на величину более двух порядков.
Аналогичные результаты для пленок серии №4 приведены здесь разделе №5, как
иллюстрация к методике измерения динамической проводимости. Так на
рис.3
приведены зависимости коэффициента отражения (кривая 1), а на рис.4 приведены
зависимости статической (1) и динамической (2) проводимостей от толщины пленки.
Можно видеть, что превышение динамической проводимости над статической при
малых толщинах достигает двух порядков. Однако приведенные на рис.4 данные не
дают возможности однозначно выяснить причину столь большого превышения, так как
в формировании приведенных там зависимостей одновременно участвуют два фактора
– состав диэлектрической матрицы ![]() и сравнительно малая
толщина – порядка
и сравнительно малая
толщина – порядка ![]() .
.
С другой стороны, в
разделе №19 на примере пленок серии №6, имеющих диэлектрическую матрицу ![]() , показано, что столь малая толщина пленок
как
, показано, что столь малая толщина пленок
как ![]() (таблица №8, пленки 03/01 и 16/01), не
может обеспечить заметного превышения динамической проводимости над статической
(не более двух раз), вследствие эффекта взаимной компенсации полей от
противоположных поверхностей пленки.
(таблица №8, пленки 03/01 и 16/01), не
может обеспечить заметного превышения динамической проводимости над статической
(не более двух раз), вследствие эффекта взаимной компенсации полей от
противоположных поверхностей пленки.
Однако приведенные в этом разделе данные опять не дают возможности сделать окончательный выбор между двумя факторами – составом диэлектрической матрицы и толщиной пленок, так как здесь оба эти фактора участвуют одновременно.
Для того, чтобы выявить
главную причину значительного (не менее чем на два порядка) превышения
динамической проводимости над статической, следует для пленок, имеющих матрицу ![]() , при которой такое превышение только и
наблюдается, исключить из рассмотрения другой фактор – малую толщину, то есть
провести измерения с той же матрицей, но на более толстых пленках.
, при которой такое превышение только и
наблюдается, исключить из рассмотрения другой фактор – малую толщину, то есть
провести измерения с той же матрицей, но на более толстых пленках.
С этой целью в настоящем
разделе будут рассмотрены пленки серии №5, имеющие толщину ![]() , что заметно превышает толщину пленок серии
№4, которая составляет
, что заметно превышает толщину пленок серии
№4, которая составляет ![]() .
.
В качестве более общего критерия возьмем не толщину пленок, а концентрацию металлической фазы, что позволит более подробно проследить влияние перколяции.
Сначала обратимся к
рассмотрению динамической проводимости, определяемой по отражению сигнала СВЧ
от пленок. На рис.11 представлена зависимость коэффициента отражения ![]() от концентрации проводящей фазы
от концентрации проводящей фазы ![]() .
.
Рис.11. Зависимость коэффициента отражения от концентрации проводящей фазы (серия №5).
Можно видеть, что зависимость имеет традиционный вид, неоднократно наблюдавшийся, например, в работах [34-36]. Сплошная кривая построена по эмпирической формуле:
![]() . (21)
. (21)
Таким образом, можно
полагать, что механизм внутригранулярной проводимости начинает формировать
динамическую проводимость пленки где-то около ![]() ,
причем пленка переходит в полностью проводящее состояние при
,
причем пленка переходит в полностью проводящее состояние при ![]()
Рассмотрим теперь, как из полученной зависимости для коэффициента отражения можно получить подобную зависимость для динамической проводимости.
В работах [34-36] в первую очередь рассматривались зависимости коэффициента отражения от толщины пленки, причем в качестве постоянного параметра выступала проводимость, входящая в качестве комплексной добавки в диэлектрическую проницаемость согласно формуле (4) (раздел №5). При этом для расчета проводимости использовалась формула (1) (там же), в которой значение проводимости подбиралось, исходя из максимального соответствия расчетного значения коэффициента отражения экспериментальному. Однако модель гранулярных токов [34], в приближении малых промежутков между гранулами (то есть вблизи перколяции, но не доходя до нее), предоставляет для расчета коэффициента отражения более простую формулу (в работе [34] приведена под номером (60)):
Формула (22) по структуре соответствует подобным формулам для коэффициента отражения, полученным в приближении малой толщины [52] или с использованием метода усреднения [53]. Приведенная в этих работах формула имеет вид:
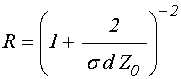 . (23)
. (23)
Отличие от формулы (22) здесь состоит
в том, что в (23) входит проводимость пленки в целом ![]() ,
тогда как в (22) – проводимость материала гранулы
,
тогда как в (22) – проводимость материала гранулы ![]() . В
работах [52, 53] формула (23) применялась для получения коэффициента отражения
от однородных чисто металлических пленок. Формула (22) выведена в работе [34]
на основе модели гранулярных токов, заведомо предполагающей пленку
неоднородной, состоящей из металлических гранул, разделенных диэлектрическими
промежутками. Формула (22) переходит в формулу (23) в случае гранул, настолько
близко примыкающих друг к другу, что промежутками между ними можно пренебречь,
то есть фактически при переходе к непрерывной среде. При этом проводимость
гранулы
. В
работах [52, 53] формула (23) применялась для получения коэффициента отражения
от однородных чисто металлических пленок. Формула (22) выведена в работе [34]
на основе модели гранулярных токов, заведомо предполагающей пленку
неоднородной, состоящей из металлических гранул, разделенных диэлектрическими
промежутками. Формула (22) переходит в формулу (23) в случае гранул, настолько
близко примыкающих друг к другу, что промежутками между ними можно пренебречь,
то есть фактически при переходе к непрерывной среде. При этом проводимость
гранулы ![]() переходит в проводимость непрерывной
среды
переходит в проводимость непрерывной
среды ![]() .
.
Из (22) проводимость выражается весьма простой формулой:
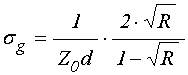 . (24)
. (24)
Таким образом, простая формула (24) для построения зависимости проводимости от концентрации металлической фазы значительно удобнее громоздкой формулы (1), поэтому представляет интерес проверки ее применимости к поставленной задаче.
Контрольная проверка с
помощью формулы (1) показала, что динамическая проводимость пленок серии №5
заключена между ![]() до
до ![]() .
Рассчитанная для обоих этих значений зависимость коэффициента отражения от
толщины по формулам (1) и (24) показала совпадение с точностью до долей
процента, тогда как при снижении динамической проводимости до
.
Рассчитанная для обоих этих значений зависимость коэффициента отражения от
толщины по формулам (1) и (24) показала совпадение с точностью до долей
процента, тогда как при снижении динамической проводимости до ![]() различие возросло до
различие возросло до ![]() . Таким образом, можно сделать вывод, что
формула (24) в предположении, что
. Таким образом, можно сделать вывод, что
формула (24) в предположении, что ![]() представляет собой
проводимость пленки в целом (то есть фактически обращаясь к формуле (23)), в
диапазоне толщин
представляет собой
проводимость пленки в целом (то есть фактически обращаясь к формуле (23)), в
диапазоне толщин ![]() , соответствующих серии №5, для
получения динамической проводимости вполне пригодна.
, соответствующих серии №5, для
получения динамической проводимости вполне пригодна.
Замечание. Следует заметить, что формула (22)
получена по модели гранулярных токов в предположении малости промежутков между
гранулами относительно их размеров. При этом, поскольку объем гранулы связан с
ее линейным размером кубической зависимостью, можно считать, что для наименьшей
из исследованных концентраций ![]() линейный размер
гранулы составляет
линейный размер
гранулы составляет ![]() При этом размер промежутка
равен
При этом размер промежутка
равен ![]() , то есть условие малости промежутка
относительно размера гранулы, хотя и с запасом довольно небольшим (примерно в
два раза), но все же выполняется, что и обеспечивает применимость формулы (24)
для расчета проводимости.
, то есть условие малости промежутка
относительно размера гранулы, хотя и с запасом довольно небольшим (примерно в
два раза), но все же выполняется, что и обеспечивает применимость формулы (24)
для расчета проводимости.
Обратимся теперь к результатам эксперимента. На рис.12 показаны зависимости статической (1) и динамической (2) проводимостей от концентрации металлической фазы. Статическая проводимость определена по методике, описанной в разделе №3, динамическая – по коэффициенту отражения с помощью формулы (24).
Рис.12. Зависимости статической (1) и динамической (2) проводимостей от концентрации металлической фазы (серия №5).
Можно видеть, что даже в
области ![]() динамическая проводимость все же
превышает статическую, хотя немного, не более чем на порядок, однако такое
превышение говорит о еще не совсем полном смыкании металлических гранул, хотя
уже и связанных непрерывными «мостиками», но по бокам от таких «мостиков» еще
остаются заметные участки диэлектрической фазы.
динамическая проводимость все же
превышает статическую, хотя немного, не более чем на порядок, однако такое
превышение говорит о еще не совсем полном смыкании металлических гранул, хотя
уже и связанных непрерывными «мостиками», но по бокам от таких «мостиков» еще
остаются заметные участки диэлектрической фазы.
Однако в области ![]() и менее превышение динамической
проводимости над статической становится тем более значительным, чем концентрация
проводящей фазы меньше. Так при
и менее превышение динамической
проводимости над статической становится тем более значительным, чем концентрация
проводящей фазы меньше. Так при ![]() превышение составляет
около двух порядков, а при концентрации
превышение составляет
около двух порядков, а при концентрации ![]() достигает
пяти порядков.
достигает
пяти порядков.
Резкого скачка
статической проводимости, соответствующего началу перколяции, не видно, однако
в соответствии с данными рис.11, можно полагать, что она наступает при ![]() Это означает, что наиболее сильное
превышение динамической проводимости над статической имеет место в условиях,
еще достаточно далеких от перколяции, когда статическая проводимость пленки в
целом, в основном, определяется проводимостью диэлектрической фазы.
Это означает, что наиболее сильное
превышение динамической проводимости над статической имеет место в условиях,
еще достаточно далеких от перколяции, когда статическая проводимость пленки в
целом, в основном, определяется проводимостью диэлектрической фазы.
Резюмируя результаты данного раздела, можно заключить, что из двух факторов, обусловливающих превышение динамической проводимости над статической решающим фактором является не толщина, а материал диэлектрической матрицы пленки.
21. Сравнение роли диэлектрической фазы для различных составов пленок
В предыдущем разделе сделан вывод о решающей роли состава диэлектрической фазы пленок в превышении динамической проводимости над статической. Представляет интерес сопоставить степень превышения с таким конкретным составом.
Трудность сложившегося положения состоит в том, что ни статическим, ни динамическим методом нельзя определить проводимость диэлектрической фазы в чистом виде, так как всегда к ней будет примешиваться какая-то часть проводимости за счет металлической фазы, так что получаемое значение будет в какой-то степени завышенным.
В рамках настоящей работы будем считать, что достаточно приемлемым приближением является такое значение проводимости, которое соответствует наименьшей концентрации металлической фазы во всех сериях исследованных пленок. То есть будем полагать, что при минимальной концентрации проводимость находится значительно ниже порога перколяции, так что постоянный ток течет, в основном, между гранулами по диэлектрической фазе, а переменный – внутри гранул по проводящей фазе.
Вообще говоря, при достаточном уменьшении концентрации проводящей фазы, зависимость той и другой проводимости должна выходить на горизонтальный участок, то есть при дальнейшем уменьшении содержания металла – не меняться. Однако четкий горизонтальный участок наблюдается только при уменьшении толщины (рис.4, серия №4), тогда как во всех остальных случаях (рис.6, серии №1, №3; рис.9, серии №7, №8; рис.12, серия №5) при минимальных концентрациях зависимости все же испытывают наклон. Однако во всех случаях та и другая проводимости при минимальной концентрации всегда меньше тех же проводимостей при максимальной концентрации, причем такое соотношение составляет от одного порядка (рис.6, серия №3) до восьми (рис.12, кривая 2, серия №5). Так что можно считать, что в любом случае проводимости при минимальных концентрациях близки к предельному (минимальному) значению.
Полученные таким образом значения проводимости для разных составов сведены в таблицу №9.
Таблица №9. Проводимости пленок разных составов.
|
Номер серии |
Состав матрицы |
Мин. мет. фаза |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
Из таблицы можно видеть,
что статическая проводимость для составов с матрицами ![]() ,
,
![]() ,
, ![]() всегда
превышает величину
всегда
превышает величину![]() (серия №2), достигая в
максимуме
(серия №2), достигая в
максимуме ![]() (серия №3), тогда как для составов с
матрицей
(серия №3), тогда как для составов с
матрицей ![]() резко падает более чем на пять порядков,
достигая
резко падает более чем на пять порядков,
достигая ![]() (серия №5).
(серия №5).
В то же время динамические
проводимости для составов с матрицами ![]() ,
, ![]() (серии №1, 2, 6, 7, 8) близки между
собой, так что меняются не более чем в полтора-два раза, и только для состава с
матрицей
(серии №1, 2, 6, 7, 8) близки между
собой, так что меняются не более чем в полтора-два раза, и только для состава с
матрицей ![]() (серия №3) изменение приближается к двум
порядкам. При этом для состава с матрицей
(серия №3) изменение приближается к двум
порядкам. При этом для состава с матрицей ![]() (серии
№4, №5) проводимости уменьшаются также всего на один-два порядка от той же
величины.
(серии
№4, №5) проводимости уменьшаются также всего на один-два порядка от той же
величины.
Особенно разительно
меняется отношение динамической проводимости к статической, приведенное в
последнем столбце таблицы. Так для составов с матрицами ![]() ,
,
![]() ,
, ![]() (серии
№1, 2, 3, 6, 7, 8) это отношение составляет от
(серии
№1, 2, 3, 6, 7, 8) это отношение составляет от ![]() до
до ![]() , тогда как для составов с матрицами
, тогда как для составов с матрицами ![]() оно достигает
оно достигает ![]() (серия
№4) и даже
(серия
№4) и даже ![]()
Таким образом, можно
видеть, что значительное превышение динамической проводимости над статической
имеет место только для составов с матрицей ![]() (серии
№4, 5), где оно составляет до четырех порядков, тогда как для всех остальных
составов превышение не превосходит нескольких единиц.
(серии
№4, 5), где оно составляет до четырех порядков, тогда как для всех остальных
составов превышение не превосходит нескольких единиц.
Если полагать, что
проводимость металлической фазы ![]() для всех составов
одна и та же (так как она образуется за счет одних и тех же металлов в одном и
том же соотношении), то из проделанного рассмотрения следует, что причина столь
сильного превышения динамической проводимости над статической состоит в крайней
малости статической проводимости диэлектрической фазы состава
для всех составов
одна и та же (так как она образуется за счет одних и тех же металлов в одном и
том же соотношении), то из проделанного рассмотрения следует, что причина столь
сильного превышения динамической проводимости над статической состоит в крайней
малости статической проводимости диэлектрической фазы состава ![]() .
.
Заключение
Исследованы статическая и динамическая проводимости аморфных наногранулированных пленок типа «металл-диэлектрик», содержащих гранулы металла, вкрапленные в диэлектрическую матрицу.
Отмечено наблюдавшееся ранее сильное (до двух порядков и более) превышение динамической проводимости над статической, имеющее место на пленках некоторых составов.
Путем анализа предшествующих работ выявлены две возможные причины столь высокого превышения – малая толщина пленок и слабая проводимость их диэлектрической матрицы.
С целью более подробного выяснения причин наблюдаемых явлений выполнено исследование динамической и статической проводимости на пленках в широком диапазоне толщин, составов и концентрации металлической фазы.
Приведены технологические
параметры и описана методика ионно-лучевого напыления пленок на лавсановой
подложке большой площади до ![]() .
.
При использовании
составных металл-диэлектрических мишеней и применении экранирования получены
пленки с вариацией параметров на единой подложке – по толщине от ![]() до
до ![]() и по
концентрации металлической фазы от
и по
концентрации металлической фазы от ![]() до
до ![]() (от
(от ![]() до
до ![]() ). Электронно-микроскопическое
исследование показало, что по морфологии пленки представляли собой
металлические гранулы
). Электронно-микроскопическое
исследование показало, что по морфологии пленки представляли собой
металлические гранулы ![]() , вкрапленные в диэлектрическую
матрицу окисла
, вкрапленные в диэлектрическую
матрицу окисла ![]() ,
, ![]() ,
, ![]() или фторида
или фторида ![]() . После
окончания роста единая подложка разрезалась на отдельные образцы (ячейки)
размером
. После
окончания роста единая подложка разрезалась на отдельные образцы (ячейки)
размером ![]() (всего из одной подложки получалось 180
образцов).
(всего из одной подложки получалось 180
образцов).
Было исследовано восемь серий образцов различных составов. По каждому образцу измерялась толщина, концентрация металлической фазы и ее относительный объем, а также статическая и динамическая проводимость.
Толщина пленок
определялась электронно-микроскопическим методам по наблюдению в торец по 15
точкам с последующим усреднением. Состав пленок и концентрация металлической
фазы определялись электронно-зондовым микроанализом путем детектирования
вторичных электронов. Относительный объем металлической фазы вычислялся исходя
из размера составляющих фазу атомов по их концентрации. Статическая
проводимость измерялась на постоянном токе двухзондовым потенциометрическим
методом. Динамическая проводимость определялась путем измерения коэффициента
отражения от пленок сигнала СВЧ в диапазоне ![]() .
.
Исследовано распределение
значений толщины по площади исходной пленки. Показано, что максимальная толщина
имеет место в центральных областях пленки, а по краям спадает более чем на
порядок. Перепад толщины между соседними ячейкам, как правило, не превышает ![]() , однако в некоторых случаях может
составлять до двух раз, что отнесено к случайным флуктуациям технологического
режима роста пленок. Отмечено, что наблюдаемое распределение значений толщины
по площади исходной пленки практически полностью (с точностью до
, однако в некоторых случаях может
составлять до двух раз, что отнесено к случайным флуктуациям технологического
режима роста пленок. Отмечено, что наблюдаемое распределение значений толщины
по площади исходной пленки практически полностью (с точностью до ![]() ) соответствует технологическому режиму,
заданному при выращивании пленок.
) соответствует технологическому режиму,
заданному при выращивании пленок.
Исследовано распределение
концентрации металлической фазы по площади исходной пленки. Показано, что по
большему размеру подложки концентрация металла монотонно возрастает до
полутора-двух раз, как это и было заложено структурой мишеней и расположением
экранов при выращивании пленок. Подобный рост концентрации имеет место и по
меньшему размеру подложки. Отмечено, что линия, соответствующая превышению
концентрации значения ![]() (
(![]() ), выше
которого должна иметь место перколяция, в основном, носит прямолинейный
характер.
), выше
которого должна иметь место перколяция, в основном, носит прямолинейный
характер.
Исследовано распределение относительного объема проводящей фазы по площади исходной пленки. Показано, что такое распределение имеет монотонный характер, подобный распределению концентрации металлической фазы.
Исследовано распределение значений статической проводимости по площади исходной пленки. Наблюдается четкая корреляция между статической проводимостью и концентрацией металлической фазы, то есть проводимость возрастает тогда, когда концентрация увеличивается. Однако зависимость проводимости от координаты, как правило, не является строго монотонной, так что по ходу перемещения по ячейкам испытывает заметные скачки. Отмечен сильный разброс значений проводимости в соседствующих ячейках, особенно увеличивающийся к краям исходной пленки. Так вблизи ее середины разброс составляет не более полутора-двух раз, тогда как к краям достигает порядка и более.
Указано, что наблюдаемый сильный разброс значений проводимости не позволяет сделать однозначный вывод о том, какой параметр больше соответствует порогу перколяции – концентрация проводящей фазы или ее относительный объем, так что более точное решение этого вопроса требует статистической обработки значительного количества материала, превосходящего возможности настоящей работы
Исследовано распределение
динамической проводимости по площади исходных пленок. Показано, что для пленки
каждого заданного состава такое распределение, в основном, соответствует
распределению металлической фазы, то есть динамическая проводимость по мере
увеличения концентрации металлической фазы также увеличивается. Разброс значений
динамической проводимости по соседствующим ячейкам значительно меньше такового
для статической проводимости и не превышает ![]() .
.
Отмечено превышение динамической проводимости над статической, составляющее для различных составов от нескольких раз до нескольких порядков. Рассмотрена интерпретация такого превышения на основе модели гранулярных токов. Показано, что оно имеет место при концентрации металлической фазы ниже порога перколяции, причем при уменьшении толщины, как правило, возрастает.
Выполнен анализ двух возможных причин высокого превышения динамической проводимости над статической – малой толщины пленок и слабой проводимости их диэлектрической матрицы.
Отмечена возможность
контроля проводимости диэлектрической матрицы по предельному значению
статической проводимости пленки в условиях минимума концентрации металлической
фазы. Выполнены измерения такой проводимости для различных составов пленок.
Показано, что диэлектрические матрицы ![]() ,
, ![]() ,
, ![]() имеют
проводимость порядка
имеют
проводимость порядка ![]() , а матрица
, а матрица ![]() имеет проводимость порядка
имеет проводимость порядка ![]() .
.
Показано, что в пленках с
довольно высокой проводимостью диэлектрической матрицы (порядка ![]() для матриц
для матриц ![]() ,
, ![]() ,
, ![]() )
уменьшение толщины ниже определенного предела (менее
)
уменьшение толщины ниже определенного предела (менее ![]() )
приводит к падению превышения вплоть до полного его исчезновения, что происходит
из-за взаимной компенсации полей на противоположных поверхностях пленок.
)
приводит к падению превышения вплоть до полного его исчезновения, что происходит
из-за взаимной компенсации полей на противоположных поверхностях пленок.
В то же время, для пленок
с низкой проводимостью диэлектрической матрицы (порядка ![]() для
матрицы
для
матрицы ![]() ) даже при толщине порядка
) даже при толщине порядка ![]() превышение динамической проводимости над
статической остается достаточно высоким (до двух-трех порядков).
превышение динамической проводимости над
статической остается достаточно высоким (до двух-трех порядков).
Сделан вывод о том, что
главной причиной значительного превышения динамической проводимости над
статической, в условиях сохранения проводимости металлической фазы на одном
уровне, является крайне низкая статическая проводимость диэлектрической фазы (в
данном случае ![]() ).
).
Благодарность
Авторы признательны с.н.с. Института геологии Коми НЦ Уро РАН, д.ф.-м.н. С.Шевчуку за помощь в определении составов пленок, а также аспиранту СыктГУ А.А.Уткину за помощь в проведении измерений статической проводимости.
Экспериментальная часть работы выполнена при финансовой поддержке МОиН РФ, проект № 1503. Теоретическая часть работы выполнении при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Суздалев И.П. Нанотехнология. Физико-химия нанокластеров, наноструктур и наноматериалов. М.: КомКнига. 2006.
2. Рит М. Наноконструирование в науке и технике. Введение в мир нанорасчета. Москва-Ижевск: НИЦ "Регулярная и хаотическая динамика". 2005.
3. Neugebauer C.A. // Thin Solid Films. 1970. V.6. P.443.
4. Gittleman J.L., Goldstain Y., Bozowski S. // Phys.Rev.B. 1972. V.5. P.3609.
5. Калинин Ю.Е., Ремизов А.Н., Ситников А.В. // ФТТ. 2004. Т.46. №11. С.2076.
6. Kotov L.N., Turkov V.K., Vlasov V.S., Kalinin Yu.E., Sitnikov A.V. // Mat.Sci.Eng. 2006.V.442. P.352.
7. Ситников А.В. Электрические и магнитные свойства наногетерогенных систем металл-диэлектрик. Диссертация на соискание ученой степени докт. физ.-мат. наук. Воронеж: ВГТУ. 2010.
8. Вендик И.Б., Вендик О.Г. // ЖТФ. 2013. T.83. №1. С.3.
9. Гуляев Ю.В., Никитов С.А., Животовский Л.В., Климов А.А., Тайад Ф., Пресманес Л., Бонин К., Цай Ч.С, Высоцкий С.Л., Филимонов Ю.А. // Письма в ЖЭТФ. 2003. T.77. №10. C.670.
10. Агранович В.М., Гартштейн Ю.Н. // УФН. 2006. T.176. №10. C.1052.
11. Parimi P.V., Lu W.T., Vodo P., Sokoloff J., Derov J.S., Sridhar S. // Phys. Rev. Lett. 2004. V.92. №12. P.127401(4).
12. Веселаго В.Г. // УФН. 1967. T.92. №3. C.517.
13. Агранович В.М., Гартштейн Ю.Н. // УФН. 2006. T.176. №10. C.1052.
14. Петров Ю.И. Кластеры и малые частицы. М.: Наука. 1986.
15. Gerber A., Milner A., Groisman B. et al. // Phys. Rev. B. 1997. V.55. №10. P.6446.
16. Казанцева Н.Е., Пономаренко А.Т., Шевченко В.Г., Чмутин И.А., Калинин Ю.Е., Ситников А.В. // Физика и химия обработки материалов. 2002. №1. C.5.
17. Kotov L.N., Efimets Yu.Yu., Vlasov V.S., Petrakov A.P., Turkov V.K., Kalinin Yu.E., Sitnikov A.V. // Adv.Mat.Rep. 2008. V.47-50. Pt.1. P.706.
18. Иванов А.В., Калинин Ю.Е., Нечаев А.В., Ситников А.В.//ФТТ. 2009. Т.51. №12. С.2331.
19. Мейлихов Е.З. // ЖЭТФ. 1999. Т.115. №4. С.1484.
20. Sheng P., Abeles B., Arie Y. // Phys.Rev.Lett. 1973. V.31. №1. P.44.
21. Abeles B., Cohen R.W., Cullen G.W. // Phys.Rev.Lett. 1966. V.17. №4. P.632.
22. Cuevas E., Ortuno M., Ruiz J. // Phys.Rev.Lett. 1993. V.71. №12. P.1871.
23. Луцев Л.В., Звонарева Т.К., Лебедев В.М. // Письма в ЖТФ. 2001. Т.27. №15. С.84.
24. Луцев Л.В., Калинин Ю.Е., Ситников А.В., Стогней О.В. // ФТТ. 2002. Т.44. №10. С.1802.
25. Луцев Л.В. // ФТТ. 2002. Т.44. №6. С.97.
26. Lutsev L.V., Yakovlev S.V. // J.Appl.Phys. 1998. V.83. №11. P.7330.
27. Луцев Л.В., Яковлев С.В. // Сб.тр. XVII Международной школы-семинара «Новые магнитные материалы микроэлектроники». 2000. М.:УРСС-МГУ. С.254.
28. Луцев Л.В., Яковлев С.В., Сиклицкий В.И. // ФТТ. 2000. Т.42. №6. С.1105.
29. Антонец И.В., Котов Л.Н., Некипелов С.В., Шавров В.Г., Щеглов В.И. // РЭ. 2004. Т.49. №10. 1243.
30. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2006. Т.51. №12. С.1481.
31. Власов В.С., Гущин Н.Н., Котов Л.Н., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // Сб. тр. XIX Международной конференции «Электромагнитное поле и материалы». 2011. М.: НИУ МЭИ. С.194.
32. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №7. №9. С.882.
33. Калинин Ю.Е., Котов Л.Н., Петрунёв С.Н., Ситников А.В. // Изв.РАН. Сер.физич. 2005. Т.69. №8. С.1195.
34. Антонец И.В., Котов Л.Н., Кирпичёва О.А., Голубев Е.А., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2014. №4. Режим доступа: http://jre.cplire.ru/jre/apr14/12/text.html, http://jre.cplire.ru/jre/apr14/12/text.pdf.
35. Антонец И.В., Котов Л.Н., Кирпичёва О.А., Голубев Е.А., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №8. С.839.
36. Антонец И.В., Котов Л.Н., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // ПЖТФ. 2014. Т.40. №14. С.1.
37. Антонец И.В., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: «НИУ МЭИ». 2014. С.111.
38. Розенберг Г.В. Оптика тонкослойных покрытий. М.: Изд. физ. мат. лит. 1958.
39. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.
40. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть четвертая. Специфические методы. Сыктывкар: ИПО СыктГУ. 2013.
41. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Материалы XXIII Всероссийской конференции «Электромагнитное поле и материалы». М.: ИНФРА-М. 2015. С.159.
42. Калинин Ю.Е., Пономаренко А.Т., Ситников А.В., Стогней О.В. // Физика и химия обработки материалов. 2001. №5. С.14.
43. Ohnuma M., Hono K., Abe T. et al. // J. Appl. Phys. 1997. V.82. №11. P.5646.
44. Калинин Ю.Е., Пономаренко А.Т., Ситников А.В., Стогней О.В. // Инженерная физика. 2003. №5. С.44.
45. Татаринова Л.И., Структура твердых аморфных и жидких веществ. М.: Наука. 1983.
46. Антонец И.В., Котов Л.Н., Некипелов С.В., Голубев Е.А. // ЖТФ. 2004. Т.74. №3. С.24.
47. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2007. Т.52. №4. С.403.
48. Антонец И.В., Щеглов В.И. Распространение волн через тонкие слои и пленки (монография). Сыктывкар: ИПО СыктГУ. 2010.
49. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.
50. Антонец И.В., Котов Л.Н., Некипелов С.В., Карпушов Е.Н. // ЖТФ. 2004. Т.74. №11. С.102.
51. Гороновский И.Т., Назаренко Ю.П., Некряч Е.Ф. Краткий справочник по химии. Киев: Наукова думка. 1974.
52. Каплан А.Е. // РЭ. 1964. Т.9. №10. С.1781.
53. Халиуллин Д.Я., Третьяков С.А. // РЭ. 1998. Т.43. №1. С.16.