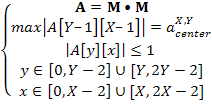АЛГОРИТМ ПОИСКА, НЕКОТОРЫЕ СВОЙСТВА И ПРИМЕНЕНИЕ МАТРИЦ С КОМПЛЕКСНЫМИ ЗНАЧЕНИЯМИ ЭЛЕМЕНТОВ ДЛЯ СТЕГАНОГРАФИИ И СИНТЕЗА ШИРОКОПОЛОСНЫХ СИГНАЛОВ

 

А. Ю. Гришенцев ¹, А. Г. Коробейников ²

¹ Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики»

² Санкт-Петербургский филиал Федерального государственного бюджетного учреждения науки Института земного магнетизма, ионосферы и распространения радиоволн им. Н.В.Пушкова Российской академии наук

 

Статья поступила в редакцию 3 мая 2016 г.

 

Аннотация. Работа посвящена исследованию некоторых свойств и методов синтеза матриц, имеющих особую форму автокорреляционной функции. В качестве элементов такие матрицы, имеют комплексные числа, модуль которых равен единице. Целью работы является отыскание, исследование некоторых свойств матриц с особой формой автокорреляционной функции. Такие матрицы позволяют: увеличить число символов алфавита кодовых последовательностей; повысить плотность энергии  синтезируемых широкополосных сигналов; реализовывать возможности скрытой (подшумовой) передачи сообщений. Авторами разработан метод отыскания матриц заданного размера на основе перебора комбинаторных вариантов и проверке значений автокорреляционной функции. Авторами статьи разработан и оптимизирован алгоритм комбинаторного поиска, исследованы некоторые свойства матриц с особой формой автокорреляционной функции. Авторами разработана компьютерная программа, с помощью которой найдены некоторые матрицы с особой формой автокорреляционной функции и приведены их характеристики. Значительное внимание уделено классификации отысканных матриц и их сравнению с некоторыми распространёнными кодовыми последовательностями, например, кодами Баркера. Рассмотрен пример практического использования матрицы с особой формой автокорреляционной функции. Рассмотренные в работе классы матриц с особой формой автокорреляционной функции предоставляют существенные возможности для скрытой, подшумовой передачи сообщений в самых различных контейнерах: от радиоэфира, до цифровых изображений. В публикации содержится значительное число практического материала иллюстрированного сравнительными таблицами и отображающими различные формы сигналов графиками и диаграммами.  В исследованиях показано: число найденных матриц достаточно велико, что предоставляет возможности для формирования значительно большего алфавита сообщений, чем, например, при использовании кодов Баркера или матриц Адамара. Существенное число отысканных матриц позволяет реализовывать дополнительные возможности, такие, например, как шифрование передаваемых сообщений за счёт смены алфавита по псевдослучайному закону, заранее известному на передающей и принимающей сторонах. Предложенные в работе методы вычислительной оптимизации позволили существенно повысить скорость отыскания матриц с особой формой автокорреляционной функции. Дополнительную информацию возможно найти на сайте одного из авторов: http://www.moveinfo.ru/.

Ключевые слова: матрицы, кодовое разделение сигналов, радиосвязь, стеганография, автокорреляционная функция.

Abstract. An investigation of some properties of matrices and methods of synthesis of particular form of the autocorrelation function is carried out. The elements of such matrices are complex numbers with the module equal to one. The aim is to fins and to study some properties of matrices with a special form of the autocorrelation function. These matrices allow to increase the number of symbols of the alphabet code sequences; to increase the energy density of the synthesized wideband signal; to pursue opportunities hidden messaging. Authors have developed a method of finding the matrix of a given size on the basis of combinatorial sorting options and check the values ​​of the autocorrelation function. We developed and optimized combinatorial search algorithm, investigated some properties of matrices with a special form of the autocorrelation function.  We have developed a computer program which permits to found some matrix with a particular form of the autocorrelation function, and given their characteristics. Considerable attention is given to the classification of the found matrices and their comparison with some common code sequences, eg, Barker codes. An example of the practical use of the matrix with a particular form of the autocorrelation function is given. The matrix classes with a special form of the autocorrelation function provides significant opportunities for hidden messaging in a variety of containers: from the radio broadcast to digital images. The publication contains a significant number of practical material illustrated by comparative tables and displays various waveform graphs and charts. The studies have shown: the number of the found matrix is ​​sufficiently large that provides opportunities for the formation of a much larger message of the alphabet, for example, than using Barker codes or Hadamard matrices. A significant number of the found matrices allows us to implement additional features, such as encryption of transmitted messages due to the change of the alphabet according to a pseudorandom, known beforehand on the transmitting and receiving sides. The proposed methods in computational optimization allowed to increase significantly the speed of finding the matrices with a special form of the autocorrelation function. Additional information may be found on the site of one of the authors: http://www.moveinfo.ru/.

Keywords: matrix, code division signals, radio, steganography, the autocorrelation function, wideband.

 

Введение

В работе «Синтез бинарных матриц для формирования сигналов широкополосной связи» [1] авторами рассмотрена актуальная задача синтеза матриц бинарных сигнатур специального вида, для которых автокорреляционные функции (АКФ) имеют высокие значения в центре (для центрального элемента) и относительно небольшие для остальных (боковых) элементов (далее АКФ специального вида). Авторы рассматривают особый класс АКФ матриц специального вида, образованных из элементов множества E₂={0,1} и вводят обозначение таких матриц МE₂. Полученные авторами результаты демонстрируют перспективность применения матриц МE₂, в первую очередь, в задачах широкополосной радиосвязи. Развитию вопросов, рассмотренных в публикации [1], посвящена данная работа. В частности, матрицы МE₂ дают достаточно хорошие значения АКФ, но при этом возможности формирования алфавита при передаче сообщений, сформированных на базе матриц МE₂, значительно ограничены относительно небольшим числом матриц заданного размера, удовлетворяющих условиям устойчивой передачи сообщений. В работе [1] также отмечено, что применение матриц МE₂ актуально для решения задач стеганографии (скрытой передачи информации) как в системах широкополосной связи, так и в других задачах, например, при встраивании информации в файл изображения [2]. Отметим, что в случае стеганографического встраивания информации в видео изображение, сформированное из потока двумерных кадров во времени (т.е. трёхмерного изображения), для встраивания информации целесообразно применять трёхмерные матрицы с характерной АКФ. Методы электротехники, теории электромагнитного поля, цифровой обработки сигналов и др. при формальном описании объектов своей предметной области работают с комплексными числами. Кроме того, ортогональность гармонических функций, применяемых для синтеза широкополосных сигналов, представляющих вещественную часть (функция cos) и мнимую часть (функция sin) комплексного числа, определяют дополнительный интерес перехода от вещественных матриц класса МE₂ к матрицам с комплексными коэффициентами. Особый интерес представляют комплексные числа, модуль которых равен единице, т.е. при z=a+jb, , где j² = –1.

Значительные достижения, полученные в последнее время в области цифровой обработки сигналов, создают дополнительный интерес к исследованию и разработке методов широкополосной передачи [3,4,5] с применением цифровой обработки [6] на базе современных вычислительных средств [7,8].

Данная работа посвящена исследованию некоторых свойств и методов синтеза матриц с АКФ специального вида, образованных из подмножества множества комплексных чисел, модуль которых равен единице.

 

Цели и задачи работы

Целью работы является отыскание, исследование некоторых свойств матриц с АКФ специального вида, позволяющих увеличить число символов алфавита кодовых последовательностей, повысить плотность энергии  синтезируемых широкополосных сигналов при сохранении возможности скрытой (подшумовой) передачи сообщений.

Задачи работы:

– определение области поиска и класса матриц с АКФ специального вида;

– оптимизация алгоритма поиска матриц с АКФ специального вида;

– сравнение и анализ некоторых характеристик полученных матриц с известными матрицами, имеющими АКФ специального вида;

– рассмотрение некоторых практических примеров эксплуатации полученных матриц.

 

Определение класса искомых матриц

Введём обозначение выбранного подмножества множества комплексных чисел, модуль которых равен единице и нулю: C₉={0, 1, –1, j, –j, 1/√2+j/√2, –1/√2–j/√2, –1/√2+j/√2, 1/√2–j/√2}. Искомые матрицы M, обозначим класс таких матриц МC₉, содержат в качестве элементов комплексные числа из множества C₉.

Выражение расчёта АКФ матриц имеет следующий вид:

,    (1)

 

где: M[Y–1–y+j][X–1–x+i]*, комплексно сопряженное число к числу M[Y–1–y+j][X–1–x+i], Y и X соответствующие размеры матрицы M.

Обозначим операцию корреляция (1) через символ «•», например АКФ матрицы M размерами Y×X будет записана как A = M•M, где матрица A размером (2Y − 1)×(2X − 1), причем центральным элементом матрицы A будет A[Y − 1][X − 1] (при отсчете элементов в A от 0 до 2Y − 2 и 0 до 2X – 2, соответственно). Искомому классу матриц с особым видом АКФ будут принадлежать матрицы, для которых, при заданных размерах Y×X матрицы M, модуль значения центрального элемента матрицы A будет максимальным, а модуль прочих элементов матрицы A не будет больше единицы:

,                                                                           (2)

где  – максимальное значение центрального элемента при заданных размерах Y×X матрицы M.

 

Алгоритм отыскания матриц с особой формой АКФ класса МC₉

Алгоритм отыскания матриц заданного размера из класса МC₉ построен на переборе комбинаторных вариантов матриц M заданных размеров Y×X, с проверкой результатов расчёта АКФ на соответствие заданным требованиям: значение центрального элемента матрицы A равно заранее выбранному значению , модуль значения боковых элементов матрицы A не превышает единицу, размеры матрицы Y×X. Алгоритм обладает значительной вычислительной сложностью, которую возможно, в асимптотической нотации [9], выразить в виде:

 O(|C₉|^X×Y),                                                                         (3)

где |C₉| – мощность множества C₉. Выражение (3) определяет наличие комбинаторного «взрыва», в результате которого отыскание матриц даже относительно небольших размеров может быть затруднено. Для оптимизации алгоритма, основного на последовательном переборе  всех возможных вариантов матриц M, которые могут принадлежать классу МC₉, воспользуемся некоторыми решениями отыскания матриц из класса МE₂, рассмотренными в работе [1], с учётом особенностей рассматриваемой нами задачи.

Из (1) понятно, что центральный элемент матрицы АКФ будет суммой произведений элементов матрицы M на элементы матрицы M^*, расположенных в одинаковых позициях. В таблице 1 приведен расчёт произведений самих на себя и на сопряженные к себе элементов множества C₉, которому принадлежат все элементы матрицы M. Очевидно, что центральный элемент матрицы АКФ будет суммой положительных вещественных чисел, а значит, вещественным положительным числом, рассчитать которое возможно по выражению:

                             (4)

 

Таблица 1. Произведение и произведение с сопряжённым комплексным числом

Комплексное число, z, (z∈C9)	Произведение, z∙z	Произведение, z∙z*
0	0	0
+1	+1	+1
–1	+1	+1
+j	–1	+1
–j	–1	+1
+1/√2+j/√2	+1j	+1
–1/√2–j/√2	+1j	+1
–1/√2+j/√2	–1j	+1
+1/√2–j/√2	–1j	+1

 

Возможно заметить, что расчёт центрального элемента по выражению (4) требует значительно меньше вычислений, чем расчёт полной матрицы АКФ. Если полученное значение центрального элемента , то это признак того, что матрица не принадлежит к классу МC₉, Учитывая, что в ходе отыскания матриц из класса МC₉ комбинаторный перебор возможных значений матрицы M при заданных размерах Y×X будет происходить последовательно, то для расчёта центрального элемента с помощью выражения (4) возможно использовать значение, вычисленное на предыдущем шаге, учтя изменившиеся на данном шаге элементы матрицы M, таким образом, количество вычислений возможно заметно сократить. Если значение центрального элемента A[Y − 1][X − 1] не удовлетворяет заданному требованию (2), то возможно переходить к проверке следующей матрицы. Если значение A[Y − 1][X − 1]  удовлетворяет заданному требованию, то необходимо вычислить АКФ для проверки значений боковых элементов матрицы A. Расчёт АКФ также возможно прервать, если значение хотя бы одного бокового элемента матрицы A по модулю больше единицы. Отметим, что встраивание условия проверки в цикл расчёта АКФ может существенно замедлить цикл, поэтому это не всегда целесообразно. Таким, образом, полный расчёт АКФ производится только для матриц, которые могут дать заданное значение центрального элемента () и для которых модуль значения боковых элементов не превышает единицу, что существенно уменьшает объем вычислений. Кроме того, умножение заранее известных комплексных чисел из множества C₉, возможно производить с помощью заранее вычисленной таблицы произведений, таким образом, затратная с точки зрения вычислений операция произведения комплексных чисел с сопряжением будет заменена операцией выборки из памяти.

Дополнительно снизить вычислительную сложность могут помочь следующие соображения. Если вычислена одна матрица из класса МC₉, то её отражением (по вертикали или горизонтали), транспонированием, возможно получить ещё семь производных от исходной матриц. Косвенным подтверждением этого является кратные восьми числа полученных матриц исследованных размеров (Y×X). Отметим, что в случае симметрии исходной матрицы относительно главной диагонали, вертикальной или горизонтальной центральных осей, некоторые полученные матрицы могут совпасть друг с другом. Также для вычислительной оптимизации, программной реализации алгоритма, полезно использовать целые форматы чисел (форматы с фиксированной точкой для мнимой и вещественной части комплексных величин). Оценка эффективности замены форматов чисел с плавающей точкой на форматы с фиксированной точкой показана в работе [2]. Значительное повышение скорости вычислений возможно обеспечить за счёт распараллеливания вычислительного алгоритма, особенно множественного распараллеливания, например, с применением GPGPU (англ. General-purpose computing for graphics processing units, что можно перевести как: неспециализированные вычисления на графических процессорах). Рассмотренные методы вычислительной оптимизации, алгоритма поиска матриц с особой формой АКФ позволяют произвести разработку алгоритма, который хорошо распараллеливается, например, с помощью разбиения перебираемых матриц на несколько групп и производства вычислений для каждой группы в отдельном потоке.

Следует отметить, что в результате комбинаторного «взрыва»  использование рассмотренных методов оптимизации не позволяет решить задачу в общем случае и поэтому вопрос отыскания матриц, даже относительно небольших размеров, из класса МC₉ остаётся открытым. Так, например, в соответствии с выражением (3), число матриц, подозрительных на принадлежность к классу МC₉, при X=Y=4, будет: 9^4×4=1853020188851841, а при X=5 и Y=4, уже: 9^4×5= 12157665459056928801.

 

Отыскание некоторых матриц из класса МC₉

Авторами был разработан алгоритм, с учетом рассмотренных выше методов оптимизации, и реализована программа отыскания матриц M из класса МC₉. В таблицу 2 сведены некоторые сравнительные характеристики матриц из классов МЕ₂ и МC₉. Плотность энергии, указанная в таблице 2, рассчитывалась как:

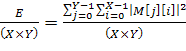.                              (5)

 

Следует отметить, что на основании сделанных исследований возможно выделить подкласс класса MC₉, в котором множество комплексных чисел имеет вид C₉–{0}={0, 1, –1, j, –j, 1/√2+j/√2, –1/√2–j/√2, –1/√2+j/√2, 1/√2–j/√2}–{0}, обозначим такое множество C₈={1, –1, j, –j, 1/√2+j/√2, –1/√2–j/√2, –1/√2+j/√2, 1/√2–j/√2}, причём C₈⊂C₉. Особенностью  матриц с особой формой АКФ, полученных из множества C₈, является более высокая плотность энергии, значение центрального элемента АКФ равно размеру матрицы (Y×X). Интересным с точки зрения исследований и дальнейшего практического применения также являются классы матриц MC₅ и MC₄ полученных из соответствующих множеств комплексных чисел C₅={0, 1, –1, j, –j} и C₄={1, –1, j, –j}, где C₅⊂C₉, C₄⊂ (C₈ and C₅).

 

Таблица 2. Сравнение характеристик некоторых матриц из класса ME₂, MC₉ и MC₈

Размер матрицы		Вещественные, из класса МE2			Комплексные, из классов МC9 и MC8
X	Y	Значение центрального элемента АКФ, acenter	Число найденных матриц, p	Отношение, acenter/(X×Y), Плотность энергии, E/(X×Y)	Значение центрального элемента АКФ, acenter	Число найденных матриц, p	Отношение, acenter/(X×Y), Плотность энергии, E/(X×Y)
1	2	2	1	1	2	64	1
2	2	3	4	0,7500	4	1536	1
1	3	2	3	0,6667	3	192	1
2	3	4	4	0,6667	5	23552	0,83
3	3	5	4	0,5556	7	266240	0,78
1	4	3	2	0,7500	4	1024	1
2	4	4	38	0,5000	7	14336	0,88
3	4	5	124	0,4167	10	14336	0,83
1	5	3	6	0,6000	5	960	1
2	5	5	20	0,5000	7	813056	0,7
1	6	3	14	0,5000	5	12416	0,83
2	6	5	132	0,4167	9	55296	0,75
1	7	4	2	0,5714	7	960	1
1	8	4	10	0,5	8	896	1
1	9	4	26	0,444	9	4096	1
1	10	4	60	0,4	10	256	1
1	11	4	110	0,3636	11	448	1
1	12	5	4	0,1190	12	256	1
1	13	5	22	0,3846	13	576	1

 

Отдельного внимания заслуживают векторы из класса MC₉, MC₈,  MC₅ и MC₄. Матрицы-векторы из классов MC₉, MC₈,  MC₅ и MC₄ возможно рассматривать как аналоги матриц-векторов (кодов) Баркера, но имеющие комплексные коэфициенты (табл. 2, 3, 4), заметим, что коды Баркера также принадлежат указанным множествам. В таблице (табл. 3) приведено число известных кодов Баркера с учётом изменения знака, для элементов кода, на противоположный и обратного порядка записи кода («переворачивания» вектора). Очевидно, что по сравнению с известными кодами Баркера, число отысканных векторов существенно больше, что предоставляет больше возможностей для формирования алфавита кодовых сообщений [10], а значит, передачи большего количества информации в единицу времени, т.е. повышению плотности передачи информации. То же возможно сказать и о матрицах из класса MC₉ (табл. 2), существенное число отысканных матриц предоставляет большие возможности для формирования алфавита кодовых сообщений.

 

Таблица 3. Сравнение характеристик векторов из класса MC₉ и MC₈ с кодами Баркера

Размер матрицы-вектора		Коды Баркера		Матрицы (векторы) из классов МC9 и MC8
X	Y	Значение центрального элемента АКФ	Число известных матриц	Значение центрального элемента АКФ	Число найденных матриц	Класс
2	1	2	4	2	64	MC8
3	1	3	4	3	192	MC8
4	1	4	8	4	1024	MC8
5	1	5	4	5	960	MC8
6	1	–	–	5	12416	МC9
7	1	7	4	7	960	MC8
8	1	–	–	8	896	MC8
9	1	–	–	9	4096	MC8
10	1	–	–	10	256	MC8
11	1	11	4	11	448	MC8
12	1	–	–	12	256	MC8
13	1	13	4	13	576	MC8

 

Таблица 4. Некоторые матрицы из класса MC₅ и MC₄

Размер матрицы-вектора		Матрицы из классов МC5 и MC4
X	Y	Значение центрального элемента АКФ	Число найденных матриц	Класс
1	2	2	16	MC4
2	2	4	64	MC4
1	3	3	16	MC4
2	3	5	384	МC5
3	3	7	1536	MC5
1	4	4	64	MC4
2	4	7	256	MC5
3	4	9	768	MC5
4	4	11	3584	MC5
1	5	5	16	MC4
2	5	7	4608	MC5
3	5	11	256	MC5
1	6	5	352	MC5
2	6	9	256	MC5
1	7	7	16	MC4
2	7	10	1408	MC5
1	8	7	160	MC5
1	9	7	496	MC5
1	10	8	1408	MC5
1	11	11	16	MC4
1	12	11	32	MC5
1	13	13	16	MC4
1	14	13	32	MC5
1	15	15	32	MC4
1	16	15	64	MC5
1	17	15	96	MC5

 

 

Пример использования матрицы размером 4×3 из класса MC₉

В качестве примера формирования широкополосного сигнала рассмотрим матрицу с особой формой АКФ размером 4×3, которая имеет вид:

.                           

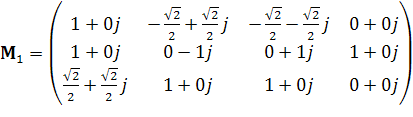Для M₁ матрица АКФ (1) имеет вид в соответствии с условием (2) (не целые значения элементов матрицы записаны с округлением):

 

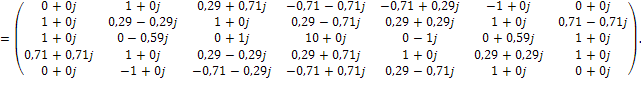
С точки зрения анализа и преобразований с понижением размерности [11] интересен также вектор, образованный суммой строк матрицы A, он имеет вид:

.

Далее синтезируем широкополосный сигнал на основе матрицы M₁, для этого примем, что вещественные части элементов матрицы будут соответствовать (синтезирующим) функциям cos(…), а мнимые части функциям j⋅sin(…), показатели функций, определяющие частоту, будут изменяться: от ω=2πf, для элементов первой строки, до 3ω=3(2πf), для элементов последней (третьей) строки, таким образом, сигнал будет образован комплексными значениями. Для удовлетворения условию ортогональности функций:

,                                   (6)

где  и  – ортогональные функции на периоде T, необходимо определять период функций кратным периоду гармонических функций 2π, при дополнительном условии равенства длительности синтезирующих функций для каждого элемента матрицы. Амплитуду синтезирующих функций будут определять соответствующие значения матрицы M₁. Таким образом, матрица, определяющая широкополосный сигнал, будет иметь вид:

.

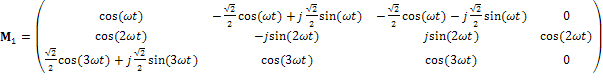Строки образованы синтезирующими функциями на изображении (рис.1). Т.к. сигнал синтезирован в цифровом виде, то аргументом являются номера отсчётов n.

 

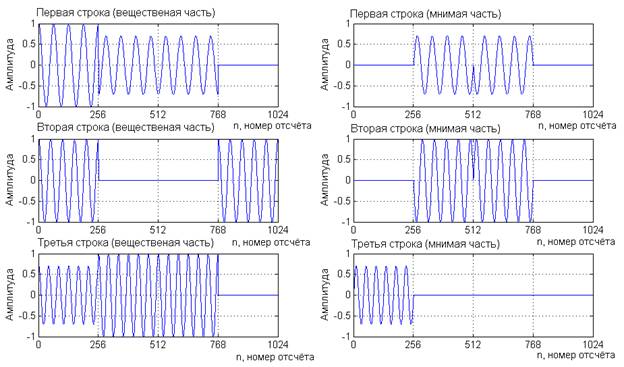
Рисунок 1. Строки матрицы, образующие широкополосный сигнал

 

Общий сигнал s(n), являющийся суммой строк (рис. 1), имеет следующий вид (рис. 2) и на фазовой диаграмме (рис. 3).

 

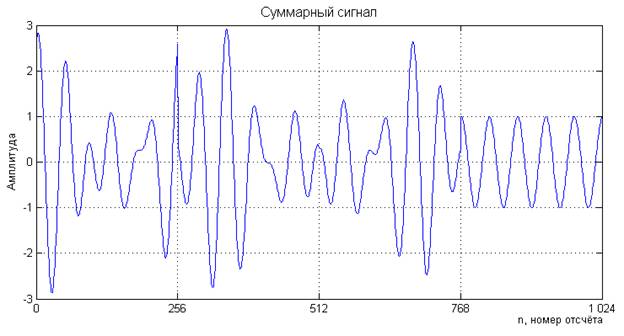
Рисунок 2. Суммарный сигнал s(n)

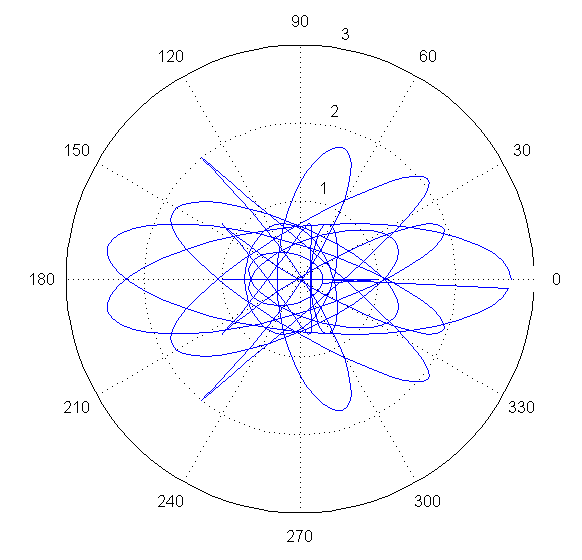
Рисунок 3. Суммарный сигнал s(n) на фазовой диаграмме

 

Обработка сигнала в приёмнике требует разделения на гармонические составляющие для возможности вычисления АКФ с учётом комплексных значений исходного сигнала. Требуется разделение на sin(…) и cos(…) гармонических составляющих, такое разделение возможно производить, например, при помощи поляризационного разделения сигналов, что показано в ряде работ [12], возможность цифрового разделения в приёмнике показана, например, в [13].

 

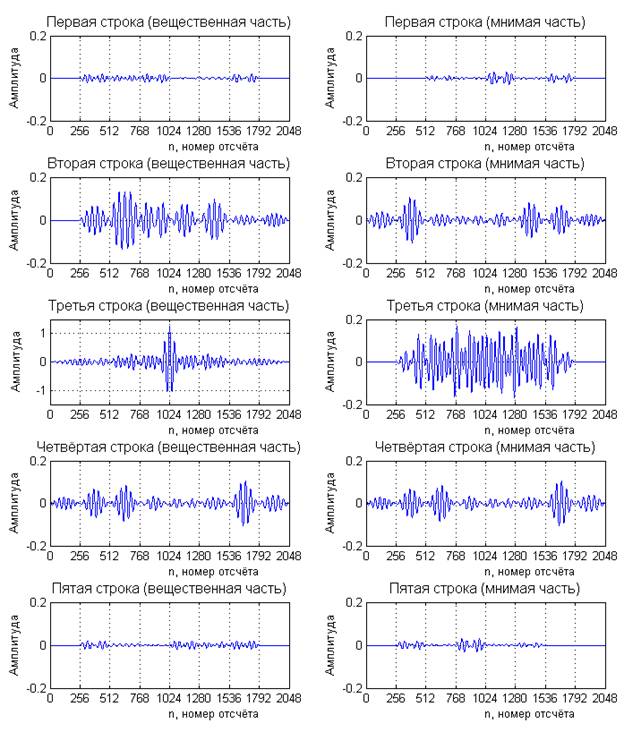
Рисунок 4. Строки нормированной АКФ, вещественные и мнимые составляющие

 

Результат вычисления АКФ для M₁ в построчном разложении приведён на изображении (рис. 4) и в виде суммы строк на изображении (рис. 5). Значения АКФ для M₁, были нормированы. Нормированная автокорреляционная функция , где N – число отсчётов сигнала s(n).

Анализ полученных результатов (рис. 4, 5) показывает, что функция АКФ имеет существенный выброс вещественных значений для центрального элемента, что хорошо видно на изображении (рис. 4, третья строка, вещественная часть), отметим, что пределы амплитуда для вещественной части третьей строки выставлены в интервале (–1; 1), в то время как для остальных элементов матрицы АКФ -  в интервале (–0.2; 0.2).

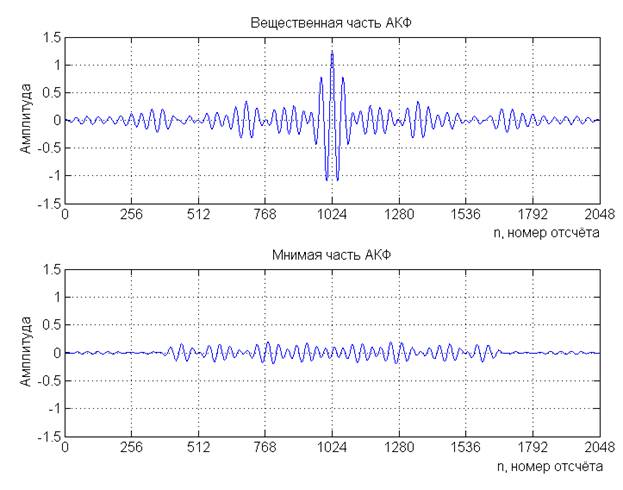
Рисунок 5. Нормированная АКФ сигнала s(n)

 

Визуализация нормированной АКФ сигнала s(n) на фазовой диаграмме (рис. 6) демонстрирует существенные выбросы при фазах πk рад (k=0,1,2,…), что соответствует максимумам косинусной (вещественной) составляющей, комплексного сигнала.

 

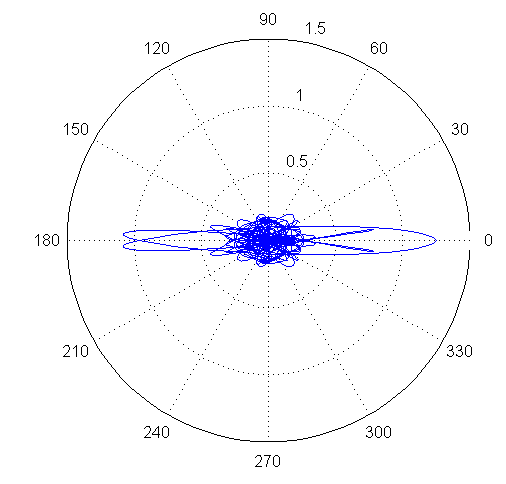
Рисунок 6. Нормированная АКФ сигнала s(n) на фазовой диаграмме

 

Некоторые замечания

Проблемой при формировании широкополосного сигнала, особенно на высоких частотах, может быть расширение спектра за счёт наличия резких изменений амплитуды по краям (назовём это явление краевым эффектом) при использовании гармонических функций cos(…) с нулевой начальной фазой на интервалах, кратных π. Устранение краевого эффекта возможно за счёт применения оконной функции w(n), причём при выборе оконной функции необходимо учитывать условие сохранения ортогональности (6), т.е.:

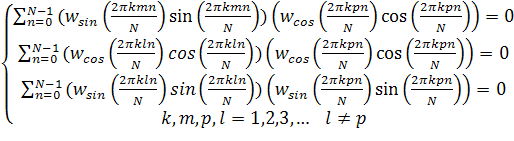,          (7)

где k определяет число периодов, m, p, l реализуют комбинаторный перебор гармонических функций на предмет проверки ортогональности.

Рассмотрение вопросов синтеза подходящих оконных функций возможно найти в специальной литературе [14].

 

Заключение

Рассмотренные в работе классы матриц с АКФ специального вида предоставляют существенные возможности для скрытой, подшумовой передачи сообщений в самых различных контейнерах: от радиоэфира до цифровых изображений. В исследованиях показано: число найденных матриц достаточно велико, что предоставляет возможности для формирования значительно большего алфавита сообщений, чем, например, при использовании кодов Баркера или матриц Адамара. Существенное число отысканных матриц позволяет реализовывать дополнительные возможности, такие, например, как шифрование передаваемых сообщений за счёт смены алфавита по псевдослучайному закону, заранее известному на передающей и принимающей сторонах. Предложенные в работе методы вычислительной оптимизации позволили существенно повысить скорость отыскания матриц с особой формой АКФ.

 

Литература

1.            Гришенцев А.Ю., Коробейников А. Г., Величко Е. Н., Непомнящая Э. К., Розов С. В. Синтез бинарных матриц для формирования сигналов широкополосной связи // Радиотехника, 2015, №9, С.: 51-58.

2.            Гришенцев А. Ю., Коробейников А. Г. Методы и модели цифровой обработки изображений – Монография. СПб: Изд-во Политехн. ун-та, 2014. – 190 с.: ил.

3.            Голдсмит А. Беспроводные коммуникации // М.: Техносфера, 2011 – 904 с.: ил.

4.            Арслан Х., Чен Чж. Н., Бендетто М. Сверхширокополосная беспроводная связь // М.: Техносфера, 2012 – 640 с.: ил.

5.            Ипатов В. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. М.: Техносфера, 2007. – 488 с.

6.            Оппенгейм А., Шафер Р. Цифровая обработка сигналов. 2-е издание, испр. М.: Техносфера, 2009. – 856 с.

7.            Герасимов И. В., Сафьянников Н. М., Якимовский Д. О. Сложно-функциональные блоки смешанных систем на кристалле: автоматизация функционального проектирования: Монография / под ред. И. В. Герасимова. – СПб.: Изд-во «ЭЛМОР», 2012. – 237 с.

8.            Жаринов О. О., Жаринов И. О. Синтез и оптимизация вычислительных алгоритмов обработки сигнала на основе корреляционно-экстремального метода в электрокардиографии высокого разрешения // Известия высших учебных заведений. Приборостроение. 2014. Т. 57. № 1. С. 29-38.

9.            Седжевик Р. Алгоритмы на C++.: Пер. с англ. – М.: ООО «И.Д. Вильямс», 2011. – 1056 с.

10.       Кудряшов Б. Д. Основы теории кодирования: учеб. пособие // СПб.: БХВ-Петербург, 2016 – 400 с.: ил.

11.       Гришенцев А. Ю., Коробейников А. Г. Понижение размерности пространства при корреляции и свертке цифровых сигналов  // Изв. вузов. Приборостроение. 2016. Т. 59, № 3. С. 211—218.

12.       Родимов А. П., Поповский В. В. Статистическая теория поляризационно-временной обработки сигналов и помех. – М.: Радио и связь, 1984.  272 с.: ил.

13.       Дятлов А. П., Кульбикаян Б. Х. Корреляционная обработка широкополосных сигналов в автоматизированных комплексах радиомониторинга // М.: Горячая линия–Телеком, 2014. – 332 с.: ил.

14.       Дворкович В. П., Дворкович А. В. Оконные функции для гармонического анализа сигналов // М.: Техносфера, 2014. – 112 с.: ил.