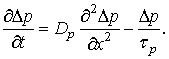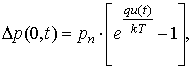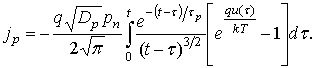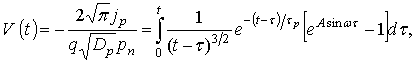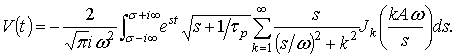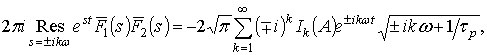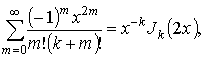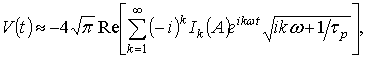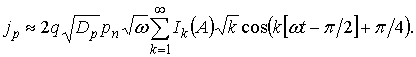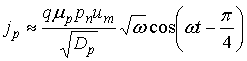УДК 621.382.2
Процессы в полупроводниковом диоде при гармоническом воздействии
Д. В. Лосев, Д. С. Бардашов, А. Г. Быков
Томский государственный университет
Статья поступила в редакцию 21 апреля 2016 г.
Аннотация. В статье на основе применения методов теории функций комплексной переменной получено решение задачи об отклике полупроводникового p-n перехода на воздействие гармонического сигнала высокой частоты. Предложенное решение демонстрирует более точное описание переходных процессов (в частности уровней кратных гармоник исходного сигнала) по сравнению с классическим рассмотрением.
Ключевые слова: полупроводниковый p-n переход, переходные процессы, диффузионное приближение.
Abstract. The solution of the problem of the response of semiconductor p-n junction on the impact of the harmonic signal of high frequency is obtained in the work. The proposed solution was created by methods of complex variable functions theory. It demonstrates a more accurate description of transient processes (in particular, levels of multiple harmonics of the original signal) in comparison with classical consideration.
Key words: semiconductor p-n junction, transient processes, diffusion approximation.
Введение
Существующая теория взаимодействия полупроводникового p-n перехода с электромагнитным полем разработана, в основном, для случая приложенного постоянного напряжения после того, как переходные процессы завершились. В случае же быстро изменяющегося сигнала, когда влияние переходных процессов является определяющим, теория развита существенно слабее и ограничивается случаями гармонического сигнала в приближении его малой амплитуды и бесконечной длительности [1] и исследованием процессов включения/ выключения или переключения диода при изменении полярности напряжения на противоположную [2].
Математическое описание переходных процессов состоит в решении дифференциальных уравнений классическим или операционным методом. Это сложная проблема, которая допускает решение только для простейших электрических цепей, в основном линейных. В случаях же цепей, содержащих большое количество элементов (особенно нелинейных), точный расчет становится невозможным, и поведение системы определяется лишь опытным путем.
В предлагаемой работе делается попытка более точного учета переходных процессов при воздействии на p-n переход гармонического сигнала высокой частоты.
Решение дифференциального уравнения
Для исследования процессов в диоде необходимо решать уравнение непрерывности в диффузионном приближении [1]
|
|
|
|
Здесь рассматривается случай плоскостного
несимметричного p-n перехода с
полуограниченной базой, где ![]() – избыточная
концентрация дырок в базе, превышающая равновесную концентрацию
– избыточная
концентрация дырок в базе, превышающая равновесную концентрацию ![]() за счет приложенного электрического поля,
за счет приложенного электрического поля,
![]() – коэффициент диффузии дырок,
– коэффициент диффузии дырок, ![]() – время жизни дырок, определяющее среднюю
длительность рекомбинационных процессов в базе. Используем условие на границе p-n перехода [1]
– время жизни дырок, определяющее среднюю
длительность рекомбинационных процессов в базе. Используем условие на границе p-n перехода [1]
где ![]() – воздействующее на диод напряжение.
– воздействующее на диод напряжение.
Решение поставленной краевой задачи легко получается с помощью метода интегральных преобразований:
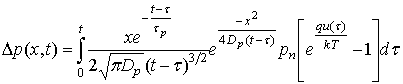 .
.
В диффузионном приближении плотность тока через p-n переход определяется его диффузионной составляющей [1]
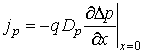 ,
,
т.е.
Случай гармонического воздействующего сигнала
Исследуем теперь зависимость плотности тока от времени при воздействии на p-n переход гармонического сигнала
период колебаний которого
много меньше постоянной релаксации среды, роль которой играет время жизни
дырок. Для этого случая непосредственное вычисление интеграла (2) численными
методами приводит к неверному результату. Это связано со сложной структурой
подынтегральной функции – быстрые осцилляции в показателе экспоненты
соседствуют с особенностью в знаменателе на верхнем пределе, наличие больших (![]() ) и малых (
) и малых (![]() )
параметров не позволяет воспользоваться простыми асимптотическими
приближениями. Непосредственное аналитическое вычисление интеграла
наталкивается на отсутствие известных интегралов, хотя бы как-то
соответствующих (2). Поэтому используем метод вычисления, основанный на
применении интегрального преобразования Лапласа к интегралу (2), рассматриваемому
как свертка оригиналов.
)
параметров не позволяет воспользоваться простыми асимптотическими
приближениями. Непосредственное аналитическое вычисление интеграла
наталкивается на отсутствие известных интегралов, хотя бы как-то
соответствующих (2). Поэтому используем метод вычисления, основанный на
применении интегрального преобразования Лапласа к интегралу (2), рассматриваемому
как свертка оригиналов.
Применение прямого преобразования Лапласа к
|
|
|
(4) |
дает
![]() ,
,
где [3]
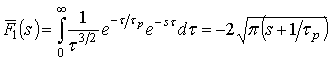 ,
,
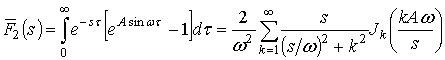 ,
,
где ![]() – функции Бесселя порядка
– функции Бесселя порядка ![]() . Обратное преобразование Лапласа приводит
к выражению
. Обратное преобразование Лапласа приводит
к выражению
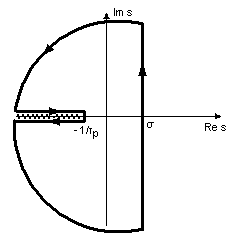
Рис. 1. Контур для вычисления интеграла (5).
Вычисление этого
интеграла производится с помощью теории вычетов [4]. Замкнем контур так, как
показано на рис. 1, и учтем, что интеграл по дуге бесконечно большого радиуса
вследствие леммы Жордана равен нулю [4], а интегралы вдоль верхнего и нижнего
берегов разреза, соединяющего точки ветвления ![]() и
и ![]() многозначной функции
многозначной функции ![]() , проходятся в противоположных направлениях, и
значения квадратного корня отличаются знаком. Тогда, согласно теореме о
вычетах,
, проходятся в противоположных направлениях, и
значения квадратного корня отличаются знаком. Тогда, согласно теореме о
вычетах, ![]() равен сумме вычетов в полюсах первого
порядка
равен сумме вычетов в полюсах первого
порядка ![]()
в существенно
особой точке ![]() и удвоенного интеграла вдоль верхнего
берега разреза, на котором принято арифметическое значение корня,
и удвоенного интеграла вдоль верхнего
берега разреза, на котором принято арифметическое значение корня,
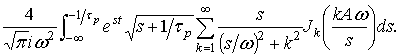
Последний интеграл
с помощью замены 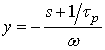 приводится к удобной для
численного интегрирования форме
приводится к удобной для
численного интегрирования форме
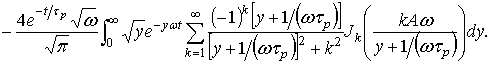
Подчеркнем, что в отличие от интеграла (2) данный интеграл не содержит особенности на промежутке интегрирования и, благодаря быстро убывающей экспоненциальной функции, допускает быстрое и устойчивое к погрешностям численное интегрирование.
Для вычисления вычета в существенно
особой точке необходимо разложить подынтегральную функцию в (5) в ряд Тейлора и
выделить коэффициенты при степени ![]() . В приближении
. В приближении ![]() последовательно получаем:
последовательно получаем:
![]() .
.
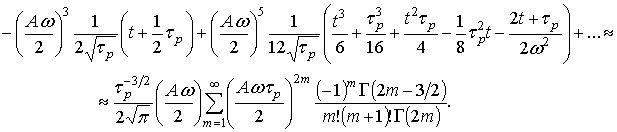
![]() .
.
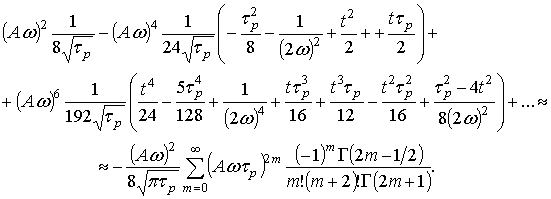
Продолжая этот процесс, приходим к выражению для вычета в форме
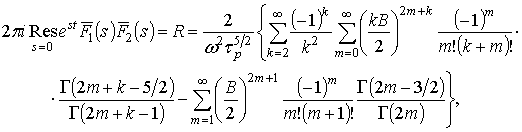
где ![]()
Полученные ряды слишком сложны для точного вычисления, поэтому сделаем небольшое приближение
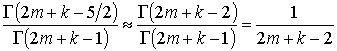 (для
(для ![]() ),
),
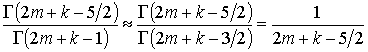 (для
(для ![]() ).
).
Тогда, используя
очевидное тождество 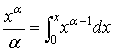 , можно представить вычет в виде
, можно представить вычет в виде
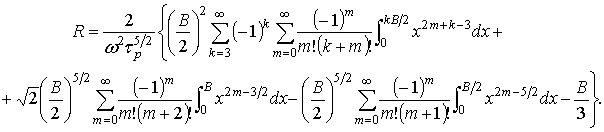
Меняя порядки суммирования и интегрирования и используя формулу [3]
|
|
|
|
получаем
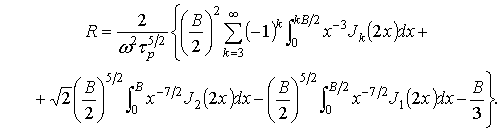
Не совершая большой погрешности, заменим верхний предел интегралов на бесконечный, и воспользуемся формулой [5]
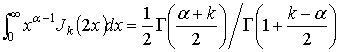 .
.
Тогда
Производя замену
индекса суммирования ![]() , используя основное свойство
гамма-функции
, используя основное свойство
гамма-функции ![]() и выражение для ряда [3]
и выражение для ряда [3]
 ,
,
а также значения ![]() ,
, ![]() [6],
окончательно получаем
[6],
окончательно получаем
 .
.
Численный расчет показывает [7],
что при выполнении условия ![]() преимущественный вклад
в
преимущественный вклад
в ![]() дает сумма вычетов (6), и
дает сумма вычетов (6), и
|
|
|
|
где ![]() – модифицированная функция Бесселя [6].
– модифицированная функция Бесселя [6].
Пренебрегая малым слагаемым ![]() в последнем выражении и учитывая, что
в последнем выражении и учитывая, что ![]() ,
, ![]() ,
,
его можно представить как
 ,
,
а плотность тока (2), протекающего через диод –
Численное моделирование и анализ результатов
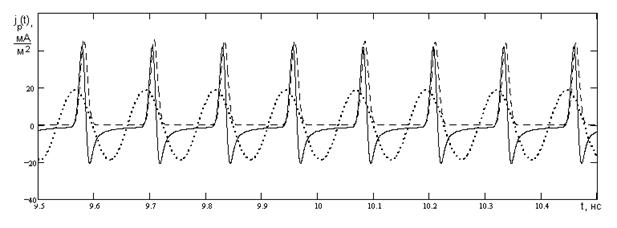
На рис. 2 представлена
рассчитанная с помощью пакета Mathcad зависимость
для сигнала (3). При этом использованы значения ![]() ,
, ![]() ГГц,
ГГц, ![]() ,
, ![]() ,
, ![]() .
Также для сравнения штриховой линией указана статическая характеристика диода,
пропорциональная (1), в которой напряжение
.
Также для сравнения штриховой линией указана статическая характеристика диода,
пропорциональная (1), в которой напряжение ![]() заменено
на сигнал (3). Для удобства восприятия она умножена на масштабный множитель
заменено
на сигнал (3). Для удобства восприятия она умножена на масштабный множитель ![]() .
.
Отметим прежде
всего существенную роль переходных процессов при быстром переключении диода, за
счет чего зависимость приобретает сложный функциональный вид. При изменении
полярности приложенного сигнала с положительной на отрицательную в начале имеет
место резкий отрицательный выброс тока, который затем стремится к значению тока
насыщения. Этот эффект давно известен, и ему дается следующее объяснение [2]:
при быстром переключении дырки не успевают рекомбинировать, и поэтому обратный
ток, который обычно мал за счет незначительного количества неосновных для ![]() -области носителей заряда, в этом случае
имеет существенную величину. Постепенно избыток дырок в
-области носителей заряда, в этом случае
имеет существенную величину. Постепенно избыток дырок в ![]() -области
уменьшается за счет рекомбинации и вытекания в
-области
уменьшается за счет рекомбинации и вытекания в ![]() -область,
и обратный ток приходит к своему статическому, малому значению. Поскольку в
момент прохождения импульса
-область,
и обратный ток приходит к своему статическому, малому значению. Поскольку в
момент прохождения импульса ![]() переход пропускает ток
в обе стороны практически одинаково и фактически не обладает выпрямляющими
свойствами, то площади под кривыми в верхней и нижней полуплоскостями
приблизительно равны.
переход пропускает ток
в обе стороны практически одинаково и фактически не обладает выпрямляющими
свойствами, то площади под кривыми в верхней и нижней полуплоскостями
приблизительно равны.
Также интерес
вызывает существенное увеличение значения тока по сравнению с низкочастотным
сигналом (на величину порядка ![]() , при используемых
параметрах приблизительно в 200 раз). Здесь имеет место похожая трактовка [2]:
за счет наличия большого количества носителей заряда, не успевающих
рекомбинировать, повышается удельная проводимость полупроводника
, при используемых
параметрах приблизительно в 200 раз). Здесь имеет место похожая трактовка [2]:
за счет наличия большого количества носителей заряда, не успевающих
рекомбинировать, повышается удельная проводимость полупроводника ![]() , (
, (![]() ,
,![]() – подвижности электронов и дырок), и,
согласно закону Ома, плотность тока.
– подвижности электронов и дырок), и,
согласно закону Ома, плотность тока.
|
|
|
Рис. 2. Зависимость jp(t) для сигнала (3). |
В заключение сравним представленное решение (7) с классическим решением, изложенным, например, в [1]. Оно получено методом комплексных амплитуд в предположении малости амплитуды воздействующего сигнала, в результате чего можно ограничиться линейными членами ряда Тейлора для экспоненты
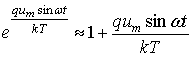 .
.
Приведем результат
для сигнала (3) при условии ![]() :
:
|
|
(8) |
что совпадает с
решением (7) при достаточно малых ![]() , для которых можно
считать
, для которых можно
считать ![]() . При этом учтено соотношение Эйнштейна
. При этом учтено соотношение Эйнштейна ![]() . Таким образом, классическое решение (8)
справедливо только при очень малых величинах входного сигнала
. Таким образом, классическое решение (8)
справедливо только при очень малых величинах входного сигнала ![]() (при этом
(при этом ![]() ). При
более высоких уровнях сигнала проявляются гармоники на кратных частотах,
благодаря чему зависимость обостряется и теряет гармоническую форму.
). При
более высоких уровнях сигнала проявляются гармоники на кратных частотах,
благодаря чему зависимость обостряется и теряет гармоническую форму.
Результат расчета по формуле (8), умноженный
на ![]() , также показан на рис. 2 пунктирной
линией.
, также показан на рис. 2 пунктирной
линией.
Таким образом, применение методов теории функции комплексной переменной позволяет точнее описывать характеристики полупроводниковых приборов при различных видах воздействующего сигнала.
Литература
1. Гаман В.И. Физика полупроводниковых приборов: Учебное пособие. – Томск: Изд-во НТЛ, 2000. – 426 с.
2. Носов Ю.Р. Полупроводниковые импульсные диоды. – М.: Сов. радио, 1965.–224 с.
3. Прудников А.П., Брычков Ю.А., Марычев О.И. Интегралы и ряды. Элементарные функции. – М.: Наука. Гл. ред. физ.-лит., 1981. – 800 с.
4. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука. Гл. ред. физ. -мат. лит. 1973. – 749 с.
5. Прудников А.П., Брычков Ю.А., Марычев О.И. Интегралы и ряды. Специальные функции. – М.: Наука. Гл. ред. физ.-мат. лит., 1983. – 753 с.
6. Справочник по специальным функциям с формулами, графиками и математическими таблицами. / Под ред. М. Абрамовица и И. Стиган. – М.: Наука, 1979. – 832 с.
7. Быков А.Г., Лосев Д.В., Бардашов Д.С. Нелинейные свойства полупроводникового диода в импульсном режиме // Сборник статей IV Всероссийской научно-технической конференции «Электроника и микроэлектроника СВЧ». СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2015, Т. 2. – С.16-20.