К ВОПРОСУ О СВЕРХРАЗРЕШЕНИИ СВЕТОЧУВСТВИТЕЛЬНЫХ МАТРИЦ

А. Ю. Гришенцев ¹, А. Г. Коробейников ², И. Б. Бондаренко ²

¹ Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики»

² Санкт-Петербургский филиал Федерального государственного бюджетного учреждения науки «Института земного магнетизма, ионосферы и распространения радиоволн им. Н. В. Пушкова Российской академии наук»

Статья поступила в редакцию 16 сентября 2016 г.

 

Аннотация. Требования к методам и средствам регистрации излучений непрерывно растут, особые требования предъявляются к приёмникам оптического излучения: повышение чувствительности, разрешения являются необходимыми требованиями современных технологий. Как известно, самым совершенным известным биологическим приёмником оптического излучения является глаз человека, глаза многих биологических существ имеют высочайшее пространственное разрешение. Многие офтальмологи считают, что здоровый глаз находится в непрерывном движении, как бы ощупывая объект рассматривания, в результате чего достигается высочайшее разрешение. За счёт движения глаз формирует динамический образ, содержащий в себе пространственное приращение яркости и/или цветности исследуемого зрительной системой объекта. Такой динамический образ является аналогом производной,  вычисленной по траектории, эквивалентной траектории движения глаза. Новейшие исследования и разработки в области электронных цифровых приёмных устройств оптического излучения показывают, что одной из актуальных задач является повышение пространственного разрешения. В то же время, повышение пространственного разрешения за счёт уменьшения линейных размеров отдельных элементов (пикселей) светочувствительных матриц затруднено тем, что при уменьшении размеров полезной площади пикселей снижается чувствительность матрицы и, соответственно, отношение полезного сигнала к шуму. Таким образом, актуальной является задача повышения пространственного разрешения при сохранении линейных размеров пикселей. Предлагается повысить разрешающую способность оптических приёмников,  сверх разрешения, которое может обеспечить электронно-оптическая система с учётом размеров светочувствительных пикселей, за счёт формирования последовательности смещённых кадров и их последующих преобразований, направленных на восстановление изображения в сверхразрешении. В работе рассмотрен способ достижения сверхразрешения светочувствительных матриц за счёт формирования и последующей обработки последовательности смещённых изображений. В статье сформулированы предпосылки к его разработке и основы предлагаемого способа, разработан математический аппарат реализации, предложены методы и средства физической реализации, выполнено моделирование предлагаемого способа в среде MatLab, приведён листинг программы и пример результатов работы программы. В заключении статьи сформулированы выводы и список используемой литературы.

Ключевые слова: сверхразрешение, светочувствительные матрицы, однопиксельная камера, обратная свёртка, цифровая обработка сигналов

Abstract. Potential methods and facilities of registration of radiation is growing. There are specific requirements for the detectors of optical radiation: high sensitivity and resolution. The most complex biological receiver of optical radiation is the human eye. Many ophthalmologists believe that a healthy eye is in constant motion, as if feeling the object of consideration. This leads to increasing of spatial resolution. Due to eye movements it is possible to form a dynamic image containing the spatial increment of the luminance and chrominance stare at the object. This dynamic image is an analogue of the derivative which is computed along a trajectory equivalent to the trajectory of the eyes motion. The latest research and development in the field of digital detectors of optical radiation show that one of the urgent tasks is to increase the spatial resolution. At the same time, increasing of spatial resolution by decreasing the linear dimensions of the pixels of the image sensor is complicated by the fact that reducing the size of the useful area of the pixel decreases the sensitivity of the matrices and, respectively, of the useful signal-to-noise ratio. Thus, the problem of improving of spatial resolution while preserving the linear size of the pixels is actual. It is proposed to increase the resolution of optical receivers due to the formation of a sequence of shifted frames and their further conversion. The goal of the transformation is the image recovery of  high resolution (super-resolution).

The article discusses the ways to achieve super-resolution image sensors due to the formation and subsequent processing of a sequence of shifted images. The article contains: the mathematical apparatus of realization, methods and tools for physical implementation, the simulation of the proposed method in MATLAB, given a program listing and an example of the results of the program.

Finally, it contains conclusions and references.

Keywords: superresolution, image sensor, single-pixel camera, deconvolution, digital signal processing.

 

Введение

Новейшие исследования и разработки в области электронных цифровых приёмных устройств оптического излучения показывают, что одной из актуальных задач является повышение пространственного разрешения. В то же время, повышение пространственного разрешения за счёт уменьшения линейных размеров отдельных элементов (пикселей) светочувствительных матриц затруднено тем, что при уменьшении размеров полезной площади пикселей снижается чувствительность матрицы и, соответственно, отношение полезного сигнала к шуму. Таким образом, актуальной является задача повышения пространственного разрешения при сохранении линейных размеров пикселей.

Развитие современных инженерных корвергентных систем подразумевает использование мультидисциплинарных технологий, методов и средств для решения задач, возникающих перед разработчиками [1]. Данная работа выполнена на стыке цифровой обработки сигналов, конструирования приёмников оптического излучения и прецизионного позиционирования.

Для дальнейших рассуждений необходимо определиться с понятием термина «разрешение» в применении к рассматриваемому вопросу. Для фотоприёмных устройств термин «разрешение» имеет достаточно много трактовок. Например, в работе [2] сказано, что понятие «разрешающая способность» относится к спектральной, пространственной и временной области. Говоря о разрешении, мы будем иметь в виду пространственное разрешение.

 

Предпосылки к возможности реализации сверхразрешения

Ещё в раннем известном труде офтальмолога Бейтса [3] и многих последующих работах [4] было показано, что глаз человека с контрастностью и разрешением, достаточным для рассмотрения мельчайших деталей, видит только тогда, когда он находится в непрерывном движении. Для того, чтобы зарегистрировать изображение объекта на сетчатке, глазу достаточно всего 1/150 секунды, при этом нормальный глаз осуществляет колоссальное количество перемещений в единицу времени, обеспечивая иллюзию непрерывного видения достаточно большого объекта. Перемещения глаза при этом могут быть произвольными и непроизвольными. Произвольные движения глаз – это движения, осуществляемые при перемещении взгляда с одной точки на другую. Непроизвольные движения глаз непрерывны, осуществляются автоматически, имеют очень маленькую амплитуду и незаметны при внешнем осмотре глаз [5].

В работе [6], показано, что при поглощении одного фотона гиперполяризация и сдвиг мембранного потенциала фоторецепторов различных представителей животного мира не одинакова. Там же приведены данные, установленные различными исследователями как порог чувствительности человеческого глаза: Вавилов С. И. установил порог 8 фотонов, Гехт С. – 6 фотонов, Пинегин Н. И. и Ван Дер Вельде – 2 фотона. Для человеческого глаза острота зрения считается нормальной (V=1.0 или 100%), если человек различает крайние точки предмета находящегося под углом в одну минуту (1´), при этом на сетчатке получается изображение около 5 мкм, что соответствует линейным размерам примерно трёх колбочек. При этом, по наблюдениям некоторых офтальмологов, у части людей наблюдается зрение существенно большей остроты: 300% и более, т.е. более разрешения, возможного при известной плотности расположения на сетчатке палочек и колбочек. При этом в ряде работ показана корреляция остроты зрения с параметрами движений глаза [7], [8] и [9].

Таким образом, возможно предположить, что для формирования образов в живых зрительных системах используются не только непосредственные объекты восприятия зрительной системы, но и объекты, формируемые нейронной сетью мозга, за счёт движения глаз и наблюдаемого пространственного приращения (дифференциала) [10] светового излучения.

Дело в том, что повышение разрешающей способности электронно-оптических приёмников за счёт уменьшения размеров фоточувствительных элементов (пикселей) матрицы ограничено фактором снижения чувствительности пикселей в результате уменьшения площади, принимающей излучение поверхности и ростом отношения сигнал/шум [11].

Предлагается повысить разрешающую способность оптических приёмников  сверх разрешения, которое может обеспечить электронно-оптическая система с учётом размеров светочувствительных пикселей, за счёт формирования последовательности смещённых кадров и их последующих преобразований, направленных на восстановление изображения в сверхразрешении.

 

Метод реализации

На рис.1 приведена последовательность получения образа (в) исходного изображения (а) с помощью с помощью светочувствительной матрицы (б), каждый пиксель матрицы формирует, как интегральную сумму падающего на неё излучения, один единственный элемент образа изображения. Очевидно, что пространственная частота в образе изображения, в соответствии с теоремой Котельникова В. А. [12], будет ограничена частотой следования светочувствительных элементов матрицы. Следует отметить, что светочувствительность каждого пикселя матрицы может быть не равномерна по его площади.

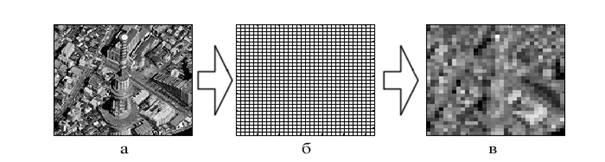
Рис. 1. Моделирование ограничения пространственной частоты при приёме изображения светочувствительной матрицей:
а – исходное изображение, б – светочувствительная матрица, в – образ изображения

Получение последовательности образов изображений (кадров), каждый из которых будет смещён относительно другого на величину, меньшую размера пикселя, и их последующее сложение с учётом смещения (рис. 2) позволяет получить большее число отсчётов в образе изображения, а значит, в соответствии с теоремой Котельникова В. А., сохранить более высокие пространственные частоты в образе изображения.

 

Рис. 2. Получение последовательности смещённых кадров: а – исходное изображение;
б – матричный приёмник излучения последовательно регистрирует изображение при различных смещениях;
в – полученные смещённые образы; г – сумма смещённых образов

На иллюстрации (рис. 2) рассмотрен пример, в котором светочувствительная матрица имеет разрешение 16x16 пикселей, каждый из которых имеет линейные размеры l_x и l_y, коэффициент заполнения 100%, для наглядности пиксели светочувствительной матрицы на изображении (рис 2, б) отделены друг от друга сеткой, смещение осуществлялось на половину линейного размера пикселя l_x/2 и l_y/2, координаты каждого пикселя при смещении матрицы, будут: (у₀, x₀), (у₀+l_y/2, x₀), (у₀, x₀+l_x/2) и  (у₀+l_y/2, x₀+l_x/2). Таким образом, получено четыре смещённых кадра.

Полученное с помощью смещения приёмной матрицы суммарное изображение  содержит больше информации, но высокие частоты подавлены фильтрами за счёт фильтрации, которую выполнил каждый пиксель, поэтому для получения сверхразрешения требуется восстановить высокочастотные составляющие.

Процедуру получения изображения с помощью смещения приёмной матрицы возможно рассматривать как свёртку с исходного сигнала-изображения с ФРТ, соответствующей ФРТ пикселя чувствительной матрицы (рис.3).

 

Рис. 3. Свёртка исходного изображения (а), с функцией рассеяния точки (б) и результат свёртки (в)

Рассмотрим случай двумерного пространства и соответственно сигналов – ,  и двумерной импульсной характеристики, чаще называемой функцией рассеяния точки (ФРТ) – , в непрерывном виде получим:

,                        (1)

где  – символическое обозначение свёртки.

В дискретном виде:

,                                                      (2)

где i и j –дискретные аналоги y и x соответственно, K и N – размеры ФРТ.

Известно, что свёртку в пространственной (временной или пространственно-временной) области возможно заменить операцией произведения спектров, что для двумерных сигналов возможно записать как:

,                                                                             (3)

где  – двумерное преобразование Фурье соответствующего двумерного сигнала,  – операция поэлементного произведения спектров.

Восстановление сигнала, полученного с помощью смещения приёмной матрицы, возможно реализовать, используя операцию обратной свёртки (deconvolution), выполненной в пространственной или в частотной области. При выполнении обратной свёртки и решении вопроса наиболее полного восстановления исходного изображения, существенной проблемой может быть определение краевой информации. Для восстановления краевой информации, возможно воспользоваться следующими решениями:

1. уменьшить размер краевых пикселей светочувствительной матрицы до размеров шага смещения;

2. использовать затемнение светочувствительной матрицы по краям так, чтобы крайние пиксели оказывались полностью в тени и принимали сигнал нулевого уровня или, точнее, сигнал, эквивалентный уровню шума при нулевом уровне полезного сигнала.

Решение (1) несколько противоречит концепции сохранения размеров элементов, образующих светочувствительную матрицу, поэтому рассмотрим в качестве примера решение (2) – затемнение краевых пикселей (рис. 4). Затемнение краевых пикселей матрицы эквивалентно затемнению краёв исходного изображения так, чтобы излучение не попадало на краевые пиксели матрицы. Восстановление изображения реализуется с помощью операции обратной свёртки, в данном примере обратная свёртка выполнена в частотной области (моделирование производилось в пакете MatLab [13]), в соответствии с выражением поэлементного деления спектральных компонент:

,                                                                                                           (4)

причём для исключения неопределённости, при крайне малых значениях , принималось, что при некотором пороговом значении (Δ) значения  равны нулю. Следует отметить, что пакет MatLab снабжен специальной функций (deconv), реализующий обратную свёртку.  В качестве значения порога выбиралось Δ=1E–32, что на десятки порядков меньше уровня значимых спектральных составляющих при амплитуде сигнала 0…255.

Рис. 4. Исходный сигнал-изображение (а) края изображения затемнены, что эквивалентно затемнению краёв матрицы; матричный приёмник излучения (б)  последовательно регистрирует изображение при различных смещениях, использовано три дискретных смещения матрицы по осям, т.е. всего девять возможных положений; суммарный сигнал, полученный при различных смещениях матрицы (в);  восстановленное в сверхразрешении изображение (г) с помощью операции обратная свёртка

 

Физическая база реализации

Существенным вопросом является технология смещения матрицы, причём для получения высокого качества результирующего изображения (в сверхразрешении) требуется высокая точность смещения матрицы. Известно, что значительные успехи в области позиционирования чувствительных элементов, преимущественно на основе пьезоэффекта, достигнуты в технологии изготовления электронных микроскопов, в частности, сканирующих зондовых микроскопов, сканирующих туннельных микроскопов и др., причём как с точки зрения осуществления смещения, так и с точки зрения детектирования смещения. Наличие такой двойной технологии позволяет не только осуществлять смещение, но и контролировать ошибку смещения, которую возможно учесть на этапе коррекции смещения и/или на этапе восстановлении изображения. Так например, группа компаний НТ-МДТ [14] предлагают электронные сканирующие устройства с прецизионными манипуляциями 5 – 50 нм [15] при характерных размерах пикселей светочувствительных матриц 2 – 50 мкм. Так например, датчик ICX205 производства Sony имеет линейные размеры пикселя 4,65×4,65 мкм [16]. Следует обратить внимание на развитие сенсорной технологии X3 (X3 Technology) производства КМОП светочувствительных матриц от компании Foveon [17], [18]. Технология X3 использует свойство электромагнитной волны, в данном случае в оптическом диапазоне, проникать на различную глубину, в данном случае в толщу полупроводника, за счёт чего регистрация различных цветовых компонент осуществляется единым пикселем, имеющим общую площадь, т.е. необходимость использования RGB фильтра Байера отпадает. Исследования Foveon показывают увеличение пространственного разрешения полноцветных изображений за счёт технологии X3 в результате отказа от фильтра Байера [19]. Матрицы, не использующие фильтр Байера, наилучшим образом подходят для реализации сверхразрешения за счёт смещения при формировании полноцветных изображений, для формирования монохромных изображений, возможно использовать другие матрицы. В частности, чувствительные элементы матриц Foveon F19, изготовленных по технологии X3, имеют линейные размеры 5,0×5,0 мкм, при смещении с шагом 50 нм возможно обеспечить 100 дискретных положений по каждому направлению, т.е. даже на основе одного единственного пикселя реализовать смещающуюся светочувствительную матрицу 100×100 с разрешением, в сто раз (по направлению) превосходящем разрешение фактически используемого светочувствительного элемента. Как видно из приведённых выше изображений (рис. 4), повышение разрешения по направлению в 2–3 раза уже позволяет получить ощутимый эффект повышения качества изображения, заметного для глаза.

Следует отметить, что способы получения многих изображений содержат в себе часть необходимых смещений для достижения сверхразрешения. Примерами могут служить: строчные движущиеся матрицы оптических сканеров, движение спутников по орбите при осуществлении дистанционного зондирования Земли (ДЗЗ) или, напротив, неподвижная система наблюдения и движущийся объект, что, например, реализуется при астрономических наблюдениях и проч. Естественно, говоря о неподвижности приёмного устройства, мы имеем ввиду относительную неподвижность, т.е. то, что оно выбрано в качестве точки отсчёта. В этих случаях часть необходимых смещений возможно реализовать за счёт установления необходимой частоты регистрации кадров таким образом, чтобы смещение наблюдаемого изображения за время, равное периоду следования кадров, происходило по плоскости приёмной матрицы вдоль строк или столбцов на величину L/p, где L – размер пикселя в направлении смещения изображения, p – целое число. При смещении изображения по плоскости матрицы более чем на один пиксель и/или при нецелом значении p, и/или при смещении изображения под углом не равным 0° или 90° к строкам (столбцам) матрицы, для получения сверхразрешения необходимы дополнительные преобразования и поправки, которые возможно реализовать с помощью вычислительных средств.

В качестве примера возможной реализации на изображении (рис. 5) приведена строчная светочувствительная матрица (содержит три строки пикселей), реализующая сверхразрешение за счёт последовательной регистрации смещённых изображений. Матрица (рис. 5) уже содержит смещённые по оси x строчки пикселей, соседние строчки смещены друг относительно друга на размер, составляющий 1/3 от линейного размера пикселя в направлении x. Коэффициент заполнения матрицы считаем равным 100%, линии, разделяющие пиксели приведены для наглядности. Матрица осуществляет движение (по стрелке) с шагом 1/3 линейного размера пикселя в направлении y, и осуществляя регистрацию строчных изображений после каждого смещения, постепенно покрывет затемнённую область. В результате формируется последовательность смещённых изображений, пригодных для восстановления исходного изображения в сверхразрешении.

 

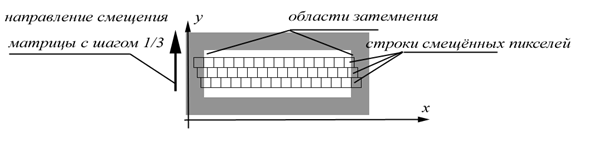
Рис. 5. Возможная реализация сверхразрешения на основе последовательной регистрации
 смещённых изображений, на основе строчной матрицы со смещёнными пикселями

 

 Как было сказано ранее, биологическим зрительным системам присущи микродвижения, и, вероятно, необходимую коррекцию для получения изображения в высоком разрешении производит биологическая нейросистема. На основании этого возможно предположить, что в области нейросетеых технологий возможно отыскание методов, позволяющих формировать изображения в сверхразрешении при помощи анализа и обработки совокупности последовательных изображений, полученных в результате несистематических смещений.

 

Модельная реализация

В качестве модельной реализации выполнено моделирование предложенного метода в среде MatLab (листинг 1), листинг программы снабжён подробными комментариями. Пример моделирования с помощью работы программы приведён на изображении (рис. 4).

Листинг 1. Моделирование получения сверхразрешения

clear all; close all; clc;   

%% загрузка данных, предварительные операции

fimg=double(rgb2gray(imread('image\7.1.02_128.bmp')));  % чтение изображения из файла

[yf, xf] = size(fimg); % определяем размеры изображения

 

% формируем импульсную характеристику

% эквивалентную импульсной характеристике пикселя

% и соответствующую числу смещений матрицы
% смещения по x и y могут быть различными

yh = 3;

xh = 3;

himp = zeros(yf,xf,'double');

himp(1:yh,1:xh) = 1/(xh*yh);

%% затемнение краёв "матрицы", через затемнение краёв изображения

fimg(1:yh, :) = 0;

fimg(end-yh+1:end, :) = 0;

fimg(:, 1:xh) = 0;

fimg(:, end-xh+1:end) = 0;

%% моделирование оцифровки, получение суммы смещённых изображений

% выполняем свёртку в пространственной области

asxy = conv2(himp, fimg);

%% моделирование восстановления изображения

sxy = asxy(1:yf, 1:xf);

% расчёт Фурье-образов сигнала и импульсной характеристики

fsxy = fft2(sxy);

fhimp = fft2(himp);

% заготовка для спектра восстанавливаемого изображения

frest = zeros(yf, xf, 'double');

% вырезаем изображение, какое получилось бы в светочувствительной матрице

smatr = asxy(yh:yh:yf,xh:xh:xf);

% циклы деления спектра сигнала на спектр импульсной характеристики

for iy = 1:1:yf

    for ix = 1:1:xf

        if( abs(fhimp(iy, ix)) <= 1E-32)  % исключение переполнения

            frest(iy, ix) = 0.0;

        else

            frest(iy, ix) = fsxy(iy, ix)/fhimp(iy, ix);

        end   

    end

end   

% восстанавливаем пространственный образ изображения по спектру

rest = real(ifft2(frest));    

%% визуализация

figure('Name','Этапы моделирования');

colormap(gray);

subplot(3,2,1);

imagesc(fimg);

title('Исходное изображение')

subplot(3,2,2);

imagesc(himp);

title('Импульсная характеристика')

subplot(3,2,3);

imagesc(smatr);

title('Эквивалент одного изображения')

subplot(3,2,4);

imagesc(sxy);

title('Эквивалент суммы изображений')

subplot(3,2,5);

imagesc(rest);

title('Восстановление изображения')

 

Заключение и выводы

В работе рассмотрен способ получения пространственного сверхразрешения на основе последовательной регистрации смещённых изображений с помощью светочувствительной матрицы. Предложена физическая и математическая основа реализации способа, выполнено моделирование.

Основными преимуществами рассмотренного метода получения сверхразрешения является:

– возможность использования светочувствительных матриц с значительной площадью отдельных светочувствительных элементов, т.е. сохранение высокой чувствительности матриц и возможность регистрации слабых сигналов за счёт существенной площади каждого светочувствительного элемента;

– относительная простота аппаратной и программной реализации на базе имеющихся технологических решений;

– возможность модернизации имеющихся оптических приёмников без изменения оптического канала преобразования сигнала;

– предлагаемая технология не ограничена датчиками оптического излучения и может быть использована для получения сверхразрешения в неоптическом диапазоне, где используются матричные приёмники излучения.

 

Литература

         1.        Герасимов И. В. Научно-исследовательская работа на кафедре САПР СПбГЭТУ «ЛЭТИ»: Материалы к научному сообщению заведующего кафедрой САПР, д.т.н., проф. Герасимова И. В. на семинаре заведующих кафедрами СПбГЭТУ «ЛЭТИ» (5 июня 2014 г.) – СПб.: Издательство СПбГЭТУ «ЛЭТИ», 2014. – 107 с.

         2.        Шовенгердт Р. А. Дистанционное зондирование. Модели и методы обработки изображений. М.: Техносфера, 2010. 560 с.

         3.        Bates W.H. The cure of defective eyesight by treatment without glasses; or, The radical cure of errors of refraction by means of central fixation.- New York: A.R.Elliott Publ. Co., 1915

         4.        Bates W. H. The Bates method for better eyesight without glasses.- New York: Holt, Rinehart and Winston, 1981

         5.        Бейтс У. Г. Улучшение зрения без очков по методу Бейтса // Переработанное издание первой книги У. Г. Бейтса «The cure of imperfect sight by treatment without glasses» (New York city. Central Fixation Publishing Company, 1920). Изд-во: «Воздушный транспорт», 1990. – 86 с.:ил.

         6.        Самойлов В. О. Медицинская биофизика. СПб: СпецЛит, 2007. 560 с.

         7.        Ярбус, А. Л. Роль движений глаз в процессе зрения / А.Л. Ярбус. – М.: Наука. – 1965. – 166 с.

         8.        Kumar, G. Characteristics of fixational eye movements in people with macular disease / G. Kumar, S.T. Chung // Invest Ophthalmol Vis Sci. – 2014. – V. 55. – No8. – P. 5125–33

         9.        Сироткина И. В., Фахретдинова Д. А., Кошелев Д. И. Острота зрения и показатели фиксации при нарушении центрального зрения различного генеза // Вестник ОГУ №12 (173), декабрь 2014 – С.: 271-275.

      10.      Гришенцев А. Ю. Эффективное сжатие изображений на базе диф-ференциального анализа // Журн. радиоэлектроники. 2012. № 11, URL: http://jre.cplire.ru/jre/nov12/1/text.pdf.

      11.      Гришенцев А. Ю., Коробейников А. Г. Методы и модели цифровой обработки изображений – Монография. СПб: Изд-во Политехн. ун-та, 2014. – 190 с.: ил.

      12.      Котельников В. А. О пропускной способности «эфира» и проволоки в электросвязи // Сб. Всесоюз. энергетический комитет. Матер. к
I съезду по вопросам и технической реконструкции дела связи и развития слаботочной промышленности. М.: Управление связи РККА, 1933.
С. 1–19.

      13.      MathWorks, MatLab URL: www.mathworks.com

      14.      Компания НТ-МДТ, URL: www.ntmdt.ru

      15.      ИНТЕГРА Прима, заголовок с экрана, язык русский, URL: www.ntmdt.ru/modular-afm/prima

      16.      ICX205 Datasheet – Sony Corporation Diagonal 8mm (Type 1/2) Progressive Scan CCD Image Sensor with Square Pixel for B/W Cameras, Sony, 22 p.

      17.      Foveon, Inc. URL:  www.foveon.com

      18.      Richard F. Lyon and Paul M. Hubel Eyeing the Camera: into the Next Century // Foveon, Inc. Santa Clara, California, USA, URL: www.foveon.com/files/CIC10_Lyon_Hubel_FINAL.pdf

      19.      Paul M. Hubel, John Liu and Rudolph J. Guttosch Spatial Frequency Response of Color Image Sensors: Bayer Color Filters and Foveon X3 Foveon, Inc. Santa Clara, California, USA, URL: www.foveon.com/files/FrequencyResponse.pdf