АДИАБАТИЧЕСКИЕ СВЕРХПРОВОДЯЩИЕ ЯЧЕЙКИ ДЛЯ энергоэффективных НЕЙРОННЫХ СЕТЕЙ

А. Е. Щеголев^1,2 Н. В. Кленов^1-5, И. И. Соловьев^3,5,6, М. В. Терешонок²

¹ МГУ имени М.В. Ломоносова, физический факультет

² Московский технический университет связи и информатики

³ МГУ имени М.В.Ломоносова, НИИ ядерной физики имени Д.В.Скобельцына
⁴ ВНИИА им. Н.Л.Духова

⁵ Московский физико-технический институт (Технический универстет)

⁶ ФГУП НИИ Физических проблем им. Ф.В.Лукина

 

Статья поступила в редакцию 16 сентября 2016 г.

 

Аннотация. Мы представляем концепцию создания базовых ячеек энергоэффективных нейросетей на основе сверхпроводящих квантовых интерферометров. Параметры двух предложенных ячеек оптимизированы для использования в составе трехслойного персептрона и сети на радиальных базисных функциях.

Ключевые слова: эффект Джозефсона, сверхпроводимость, искусственная нейронная сеть, нейрон, функция активации, РБФ-сеть, Sigma-cell, S-cell, Gauss-cell, G-cell.

Abstract. Superconducting digital systems are considered recently as one of the most promising options for the physical implementation of fast and energy-efficient artificial neural networks. Possibility to combine advantages of Josephson active antenna structures, amplifiers and analog-to-digital converters together with neural network circuits in complexes for cognitive signal processing is of particular interest. 
We propose physical foundations for a new energy efficient implementation of artificial neural network algorithms. We describe two neuron cells: Sigma-cell and Gauss-cell with sigmoid- and Gaussian-like activation functions respectively. We developed simple theory to optimize their transfer (flux-to-current) functions for
application in three-layer perceptron and radial basis functions networks. Design of these cells is inspired by adiabatic quantum flux parametron; the both have simple topology and low energy consumption, working in superconducting regime. Maintained similarity of designs allows to use well-developed adiabatic superconductor logic cells in interface circuits. 

Key words: Josephson effect, superconductivity, artificial neural network, neuron, activation function, RBF network, Sigma-cell, S-cell, Gauss-cell, G-cell.

Введение

В 1961 году Фрэнк Розенблатт впервые представил миру электронную машину «Марк-1» – первый нейрокомпьютер, работающий по схеме персептрона [1] с использованием трех видов базовых элементов, образующих (1) слой сенсоров (или рецепторов), сигнал от которых передается на (2) слой ассоциативных элементов (искусственных нейронов), а затем – на (3) слой реагирующих элементов. Такое устройство персептрона позволяет создать набор «ассоциаций», которые задают соответствие между входящими импульсами и импульсом выходящим (реакцией). Каждый искусственный нейрон обладает своей функцией активации или функцией возбуждения, которая вычисляет его выходной сигнал. И на сегодняшний день построенные по таким принципам искусственные нейронные сети (ИНС) начинают играть заметную роль для решения, к примеру, проблемы распознавания (образов, типов  и источников сигналов и т.д.) в системах спутниковой и сотовой связи, радарных системах, комплексах управления беспилотными транспортными и летательными средствами.

С другой стороны, в области аналоговой и цифровой сверхвысокочастотной (быстродействующей) электроники для телекоммуникаций в последние годы интенсивно развивается направление, связанное с использованием энергоэффективных сверхпроводниковых технологий. Использование специфики таких квантовых явлений как эффект Джозефсона и макроскопическая квантовая интерференция позволило создать достаточно чувствительные электрически-малые активные антенны [2], усилители-преобразователи для магнитной компоненты детектируемого сигнала и аналого-цифровые преобразователи для него же [3,4]. Попытки объединить сильные стороны джозефсоновских комплексов, обеспечивающих прием и первичную обработку информации, и нейросетевых алгоритмов предпринимались достаточно давно [5-13]. К сожалению, основная часть предложенных решений предполагает переход в процессе функционирования джозефсоновских контактов в резистивное состояние (с отличным от нуля средним значением падения напряжения на элементе), что существенно ограничивает возможности для увеличения общей энергоэффективности, открываемые за счет использования сверхпроводниковой технологии. В рамках данной работы мы предлагаем решение указанной проблемы за счет творческого использования концепции так называемых сверхпроводящих адиабатических логических цепей [14-21].

1. Sigma-cell: базовый элемент многослойного персептрона

Базовым элементом для предлагаемой реализации сверхпроводящих искусственных нейронов является хорошо известный квантрон (рисунок 1а), превращающий приложенный к контуру магнитный поток Ф_X (входной сигнал) в ток I_out, циркулирующий в кольце с индуктивностью L_q (выходной сигнал). Здесь и далее мы будем пользоваться нормированными величинами , , , где  – квант магнитного потока.

 

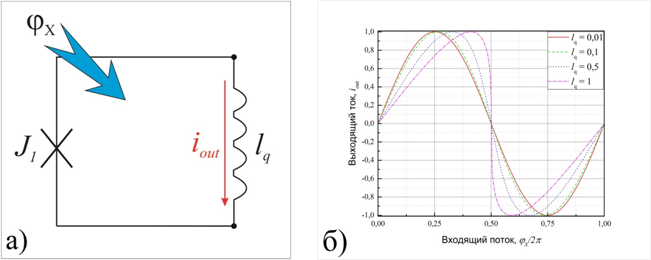
Рисунок 1. а) Схематическое изображение квантрона.

б) Ток-потоковое преобразование в  квантроне для различных значений индуктивности кольца l_q.

 

Ток-потоковое преобразование квантрона можно представить в виде аналитического выражения из уравнения для баланса фаз сверхпроводящего параметра порядка в кольце (здесь φ – падение такой фазы на единственной джозефсоновской гетероструктуре, для которой ток-фазовую зависимость мы положили синусоидальной):

                        (1)

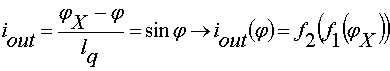           (2)

Для решения задач, например, распознавания образов или изображений в схеме персептрона используют сигмоидальную функцию активации, как наиболее математически удобную для алгоритмов обучения сети [1]. Для того, чтобы нужным образом изменить вид ток-потокового преобразования, введем в состав квантрона дополнительные сверхпроводящие контура [22, 23]. Простейший двухконтурный сверхпроводящий квантовый интерферометр с преобразованием магнитного потока на входе в ток в индуктивности L_q на выходе в виде сигмоидальной функции (Sigma-cell  или S-cell) представлен на рисунке 2 как часть слоя ассоциативных элементов трехслойного персептрона.

 

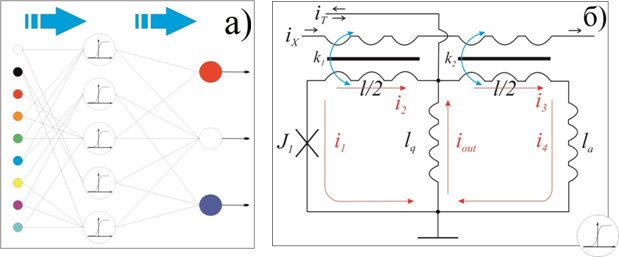
Рисунок 2. а) Схематическое изображение трехслойного персептрона с сигмоидной функцией активации.

б) Принципиальная схема Sigma-cell.

 

Справедливость сделанного утверждения можно показать, получив – по аналогии с квантроном – для S-cell ток-потоковое преобразование. Для этого нужно записать правила Кирхгофа и условия баланса фаз в сверхпроводящих контурах (все используемые далее обозначения введены на рисунке 2б).

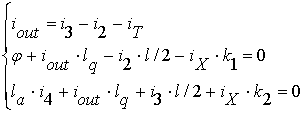                               (3)

Приводим второе уравнение из (3) к следующему виду:

                    (4)

Третье же уравнение системы (3) приводим к виду

                (5)

Теперь, подставляя ток i₃ из (5) в (4), приходим к следующему выражению:

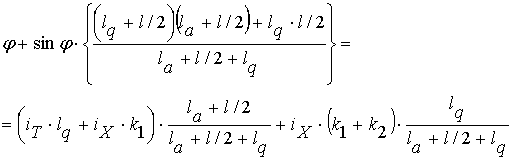(6)

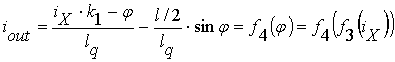,                         (7)

 

Графическое представление полученного выражения можно найти на рисунке 3 для различных параметров предлагаемого базового элемента трехслойного персептрона.

Из рисунков 3а и 3б видно, что при увеличении индуктивности l_q амплитуда отклика уменьшается, а совпадение с аналитическим выражением для сигмоидальной функции ухудшается. Это означает, что для построения оптимальной искусственной нейросети необходимо минимизировать величину «выходной»  индуктивности. Для значения l_q=0.1 (ограничивающего снизу диапазон реализуемого на практике), были построены графики, изображенные на рисунках 3в и 3г: изменение таких параметров системы как l_a или α=k₁/k₂ позволяет управлять общим наклоном ток-потокового преобразования. Функция активации, наиболее близкая к сигмоидальной, и тем самым представляющая для нас наибольший интерес, образуется для параметров системы l_a=1, l=0.6 и k₁=k₂=0.1.

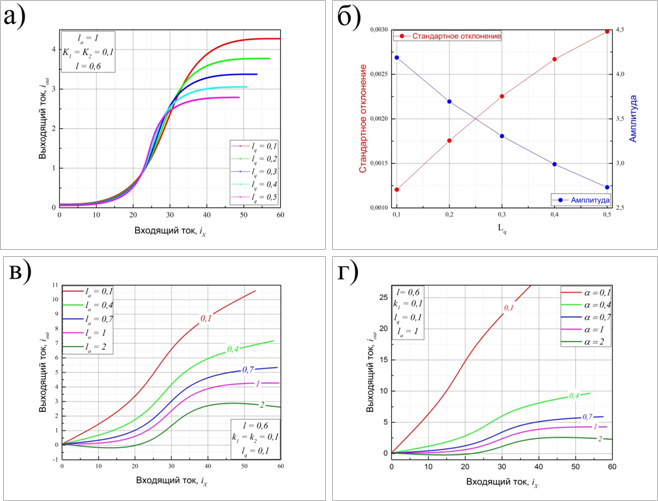
Рисунок 3. а) Ток-потоковые преобразования в S-cell как функция параметра l_q; б) Зависимость стандартного отклонения от сигмоидальной функции и зависимость амплитуды выходной характеристики как функции индуктивности l_q; в) и г) Ток-потоковое преобразование S-cell для различных значений параметров l_a и α=k₁/k₂ соответственно (l=0.6, l_q=0.1).

2. Gauss-cell: базовый элемент сетей на радиально-базисных функциях

Для ряда практически важных задач телекоммуникаций (например, для  идентификации различных источников в системах когнитивного радио) искусственная нейронная сеть на основе персептрона не является оптимальной, так как для формирования конечного сигнала на выходе требуется участие почти всех нейронов сети (глобальная аппроксимация входного сигнала) [24, 25]. Также для решения подобных задач потребовалось бы слишком долгое обучение и сложная сеть взаимодействующих нейронов.

Однако существует другой подход, который заключается в отражении входного множества импульсов во множество выходных значений посредством использования только некоторых одиночных нейронов. Каждый из этих нейронов отвечает за свою область пространства входящих импульсов. Подобный метод носит название вероятностного подхода, где в качестве функций активации нейронов используются функции Гаусса.

Самыми распространенными сетями, работающими на данном принципе, являются сети на радиальных базисных функциях (РБФ-сети). При использовании такого подхода объекты классифицируются на основе оценок их близости к соседним образцам. В основу классификации в РБФ-сети положено использование методов Байеса. Идея метода состоит в том, что для каждого образца можно принять решение на основе выбора наиболее вероятного класса из тех, к которым мог бы принадлежать этот образец. Такое решение требует оценки функции плотности вероятностей для каждого класса. Эта оценка получается в результате рассмотрения учебных данных. Формальным правилом является то, что класс с наиболее плотным распределением в области неизвестного экземпляра будет иметь преимущество по сравнению с другими классами. Традиционный подход к оценке плотности вероятности для каждого класса состоит в предположении о том, что плотность имеет некоторый определенный вид – чаще всего используется нормальное распределение, поскольку оно позволяет оценить такие параметры модели, как среднее и стандартное отклонение, аналитически.

Принципиальная схема предлагаемой нами ячейки Gauss-cell (или G‑cell), которая реализует гауссоидную функцию активации,  представлена на Рисунке 4. Схема G-cell, схожая с адиабатическим квантовым параметроном (АКП), по сути, является двухконтактным интерферометром с шунтирующей индуктивностью l_q. Как и в случае S-cell внешний ток i_X прикладывается к управляющей линии, связанной с симметричными плечами интерферометра (l/2 и l/2) магнитным образом (см. Рисунок 4б).

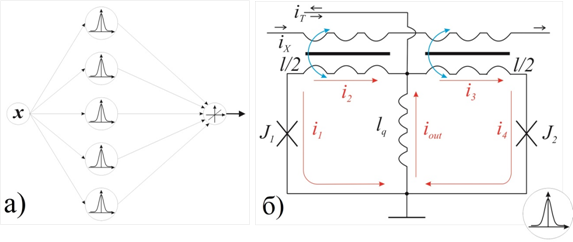
Рисунок 4. а) Схематическое изображение организации РБФ-сети. б) Принципиальная схема Gauss-cell.

 

Запишем уравнения для G-cell (основываясь на уравнении Кирхгофа и балансе фаз, все используемые далее обозначения введены на рисунке 4б):

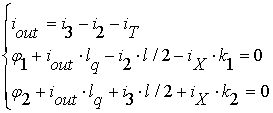.                             (9)

Далее складываем оба уравнения для фаз и делим на два, получаем:

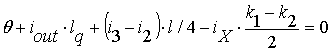,                    (10)

где  – фаза, которую мы назовем суммарной. Несложными алгебраическими операциями, с целью оставить в уравнении переменную только одного типа, а именно джозефсоновскую фазу, приходим к следующему уравнению для суммарной фазы:

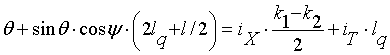.        (11)

 

Аналогичным образом получается уравнение для разностной фазы (когда мы вычитаем уравнения для фаз друг из друга):

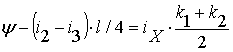                              ,                                    (12)

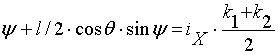,                       (13)

где  фаза, которую мы назвали разностной.

Таким образом, мы получаем параметрические функции вида:

, .

Несложным образом выписывается выражения для тока i_out:

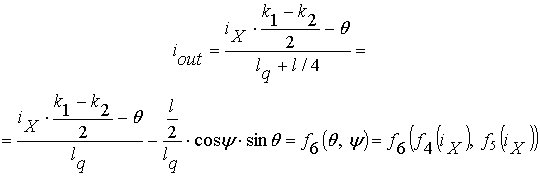   (14)

Ток-потоковые преобразования в G-cell представлены на рисунке 5. Выбор значения индуктивности в системе определяется балансом между амплитудой отклика и его среднеквадратичным отклонением от математической Гаусс-функции. Как видно из приведенных ниже графиков, при увеличении индуктивности l или l_q амплитуда также увеличивается, но совпадение с функцией Гаусса уменьшается, что порождает задачу оптимизации параметров ячейки под требования конкретной реализации РБФ-сети.

 

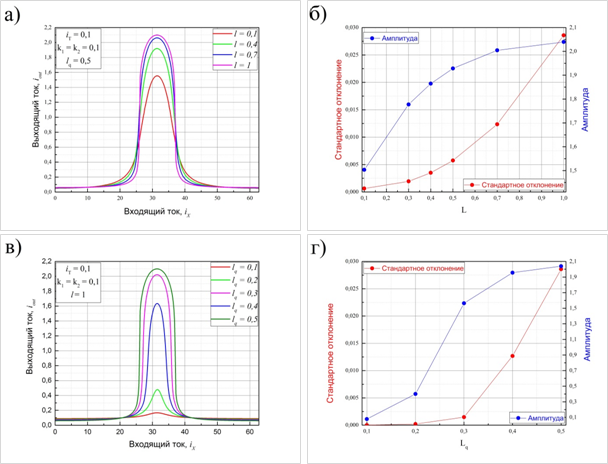
Рисунок 5. Выходные характеристики G-cell (для различных значений параметров l и l_q а) и в) соответственно)

 и графики зависимостей стандартного отклонения и амплитуды б) и г).

 

3. Выводы

Представлена концепция создания базовых ячеек нейросетей на основе элементов, используемых в предельно энергоэффективной на сегодняшний день адиабатической логике. В перспективе представляется интересной возможность объединения в одном комплексе для приема и обработки информации

1)                детекторов магнитной компоненты сигнала на основе сверхпроводящего квантового интерферометра, уже давно продемонстрировавших свой уникальный потенциал;

2)                на той же технологической базе построенных ток-потоковых преобразователей, подобных описанным здесь элементам S-cell и G-cell, связанных магнитным образом в единую сеть при помощи методов, описанных, например, для сверхпроводящих адиабатических логических цепей [16-21, 11].  Объединение на одном чипе (или хотя бы в одном криогенном комплексе) и уникальной приемной системы (рабочая частота которой может достигать сотни ГГц), и логических цепей, обеспечивающих первичную обработку (классификацию) поступающих данных, обещает вдобавок ко всему прочему и резкое уменьшение потерь и задержек на соединениях между различными частями телекоммуникационной системы.

Благодарности

Работа выполнена при поддержке гранта президента РФ MK-5813.2016.2, гранта РФФИ 16-29-09515-ofi_m и гранта для ведущих научных школ 8168.2016.2.

Литература

1.            Rosenblatt F.X. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books, Washington DC, 1961.

2.            Soloviev I.I., Kornev V.K., Sharafiev A.V., Klenov N. V., Mukhanov O. A. // IEEE Trans. Appl. Supercond. 2013. V. 23. N. 3. P. 1800405.

3.            Spietz L., Irwin K., Aumentado J. // Appl.Phys.Lett. 2009. V. 95. P. 092505.

4.            Mukhanov O. A. History of Superconductor Analog-to-Digital Converters In 100 Years of Superconductivity. Rogalla H., Kes P., Eds; London, 2011.

5.            Yan Q., Li M., Chen F., Jiang T., Lou W., Hou T.Y. Lu C.-T. // IEEE Trans. Wireless Commun. 2014. V. 13. P. 5893.

6.            Munjuluri S., Garimella R.M. // Procedia Comput. Sci. 2015. V. 46. P. 1156.

7.            Farooqi M., Tabassum S., Rehmani M., Saleem Y. J. // Network Comput. Appl. 2014. V. 46. P. 1–16.

8.            Crotty P., Schult D., Segall K. // Phys. Rev. E, 2010. V. 82. P. 011914.

9.            Harada Y., Goto E. // IEEE Trans. on Magn. 1991. V. 27. P. 2863–2866.

10.       Rippert E.D., Lomatch S. // IEEE Trans. Appl. Supercond. 1997. V. 7. P. 3442–3445.

11.       Chiarello F., Carelli P., Castellano M.G., Torrioli G. // Supercond. Sci. Technol. 2013. V. 26. P. 125009.

12.       Yamanashi Y., Umeda K., Yoshikawa N. // IEEE Trans. Appl. Supercond. 2013. V. 23. P. 1701004.

13.       Onomi T., Nakajima K. // J. Phys.: Conf. Series. 2014. V. 507. P. 042029.

14.       Likharev K. // IEEE Trans. Magn. 1977. V. 13, 1. P. 242–244.

15.       Hosoya M., Hioe W., Casas J., Kamikawai R., Harada Y., Wada Y., Nakane H., Suda R., Goto E. // IEEE Trans. Appl. Supercond. 1991. V. 1. P. 77–89.

16.       Semenov V.K., Danilov G.V., Averin, D.V. // IEEE Trans. Appl. Supercond. 2007. V. 17. P. 455 - 461.

17.       Takeuchi N., Yamanashi Y., Yoshikawa N. // Appl. Phys. Lett. 2013. V. 102. P. 052602.

18.       Nagasawa S., Hashimoto Y., Numata H., Tahara S. // IEEE Trans. Appl. Supercond. 1995. V. 5. P. 2447-2452.

19.       Nagasawa S., Hinode K., Satoh T., Akaike H., Kitagawa Y., Hidaka M. // Physica C. 2004. V. 412-414. 2. P. 1429-1436.

20.       Takeuchi N., Yamanashi Y., Yoshikawa N. // Supercond. Sci. Technol. 2015. V. 28. P. 015003.

21.       Takeuchi N., Yamanashi Y., Yoshikawa N. // J. Appl. Phys. 2015. V. 117. P. 173912.

22.       Kornev V.K., Soloviev I.I., Klenov N.V., Mukhanov O.A. // Supercond. Sci. Tech. 2009. V. 22. P. 114011.

23.       Kornev V.K., Soloviev I.I., Klenov N.V., Mukhanov O.A. // IEEE Trans. Appl. Supercond. 2007. V. 17, 2. P. 569-572.

24.       Adjemov S.S., Klenov N.V., Tereshonok M.V., Chirov D.S. // Moscow University Phys. Bull. 2015. V. 70, 6. P. 448–456.

25.       Adjemov S.S., Klenov N.V., Tereshonok M.V., Chirov D.S. // Programming and Computer Soft. 2016. V. 42, 3. P. 121–128.

26.       S. S. Adjemov, N. V. Klenov, M. V. Tereshonok, D. S. Chirov // Moscow University Phys. Bull. 2016. V. 71, 2. P. 174–179.