| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8 , 2000 |
ВЗАИМОДЕЙСТВИЕ МОЩНОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ С ТОНКИМ ПЛАЗМЕННЫМ СЛОЕМ
С.Л. Зиглин*, А.С. Ильин*, В.В. Кулагин**, В.А. Черепенин*
1. Институт Радиотехники и Электроники РАН, Москва
2. Государственный Астрономический институт
им. П. К. Штернберга МГУ им. М. В. Ломоносова, Москва
Получена 16 Августа 2000 г.
С помощью самосогласованного метода анализа исследовано взаимодействие линейно-поляризованной электромагнитной волны с плотным плазменным слоем. Показано, что при падении мощной гармонической волны на тонкий плазменный слой отраженное поле может иметь вид ультракоротких разнополярных импульсов излучения с амплитудой, значительно превосходящей амплитуду падающей волны. Рассмотрен также процесс взаимодействия плазменного слоя со стоячей электромагнитной волной и получено обобщение классических результатов о характере движения электронов в высокочастотном поле на случай сильного поля и большого радиационного трения. В сильном высокочастотном поле происходит расщепление минимума эффективного потенциала на два новых, что приводит к нарушению зеркальной симметрии излучения плазменного слоя.
Введение.
В последнее время большое внимание уделяется проблемам получения мощных ультракоротких импульсов и когерентного электромагнитного излучения высоких (вплоть до рентгеновских) частот
с помощью взаимодействия сверхмощного лазерного излучения с твердой мишенью [1-6]. Причина появления высших гармоник в спектре отраженного сигнала состоит в том, что при падении мощной электромагнитной волны с интенсивностью![]() ,
,
где
Существенные результаты, описывающие процесс отражения мощной (ультрарелятивистской) волны от плазменного слоя, могут быть получены в рамках модели электронных листов
[8]. Эта модель даёт последовательное микроскопическое описание взаимодействия плазменного слоя и электромагнитной волны и позволяет решать многие самосогласованные задачи о взаимодействии полей с заряженными средами. Особенно простые уравнения движения получаются в случае малой толщины плазменного слоя (значительно меньше длины волны падающего излучения), когда в модели можно ограничиться одним листом. Именно этот случай и будет подробно проанализирован в настоящей работе.В частности, будет показано, что при ультрарелятивистских амплитудах внешнего поля отраженная волна имеет существенно негармонический характер: происходит синхронное излучение гармоник частоты падающей волны. Именно, синусоидальная падающая волна может преобразовываться в последовательность разнополярных коротких импульсов электромагнитного излучения большой амплитуды. При этом за счет обогащения гармониками происходит уменьшение длительности отдельного импульса, а амплитуда импульсов может существенно превышать амплитуду падающей волны. Будет рассмотрен также процесс взаимодействия плазменного слоя со стоячей линейно-поляризованной электромагнитной волной и получено обобщение классических результатов о характере движения электронов в высокочастотном поле
[9] на случай сильного поля и большой концентрации электронов (большого радиационного трения). Оказывается, что в сильном высокочастотном поле (Для простоты в дальнейшем анализе будем считать ионный фон неподвижным, а концентрацию электронов в плазме достаточно большой, так что частота внешнего поля будет значительно меньше плазменной частоты. Кроме того, будем считать, что электроны в начальный момент времени покоятся (приближение холодной плазмы).
Следует отметить, что отражение от электронных (плазменных) зеркал может сопровождаться также изменением статистики отраженного поля (генерацией неклассических состояний электромагнитного поля), причем эффективность процесса растет с увеличением мощности падающей волны [10], однако, в настоящей работе эта проблема не будет затрагиваться.
1. Модель и основные уравнения.
Рассмотрим заряженную среду, однородную в направлениях, перпендикулярных оси
Oz. В этом случае плотности зарядаПусть теперь имеется тонкая заряженная плоскость, образованная бесконечно протяженным в x и y-направлениях слоем электронов, толщина которого значительно меньше длины волны падающего излучения. В этом случае слой эквивалентен бесконечно тонкому листу, для описания динамики которого достаточно задать 3+1- функции времени: три компоненты скорости
Рис.1. (3+1)-модель электронного листа.
Плотности заряда и тока такого листа имеют вид:
где
Подставляя теперь выражения (2) в уравнения (1) и интегрируя по
где,
Заметим, что выражения (3) являются одномерными (или, точнее, 3+1- мерными) аналогами классических решений Лиенара – Вихерта
[7] и дают точное выражение для поля, создаваемого бесконечной плоскостью, при этом компонентуПолучим еще выражение для спектральных компонент поля излучения
Подставляя теперь в (4) выражение для поля (1), получим
где
Для спектрального разложения поля излучения электронного листа получим, подставив в (5) выражение для плотности тока
При периодическом (с периодом
Рассмотрим теперь влияние поля излучения (3) на движение электронного листа. Из выражений (3) следует,
что взаимодействие электронного листа с собственным полем излучения приводит к появлению удельной силы самодействия [8]:т.е. появляется эффективная "вязкая
" сила (8) с постоянным коэффициентом вязкости для поперечного движения и нелинейным
коэффициентом вязкости
для поперечного движения и нелинейным
коэффициентом вязкости 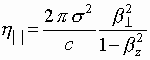 для продольного движения.
для продольного движения.
Уравнения движения для отдельного электрона этого листа в однородных по
x и y поляхЗдесь
2. Заданное продольное движение плазменного листа.
Пусть сначала продольное движение листа является заданным:
Пусть для простоты плотность заряда
Заметим, что выражение для амплитудного доплеровского фактора
Пусть теперь зависимость продольной скорости от времени определяется выражением
Рис.2. Форма
отраженного поля ![]() при различных значениях амплитуды скорости
плазменного зеркала: а.)
при различных значениях амплитуды скорости
плазменного зеркала: а.)![]() ;
б.)
;
б.)![]() ;
в.)
;
в.)![]() .
.
В отраженной волне присутствует большое
число нечетных гармоник основной частоты ![]() ,
причем, чем ближе
,
причем, чем ближе ![]() к единице, тем больше гармоник
задействовано в формировании отраженной
волны. Принципиальным моментом является
жесткая привязка фазы всех гармоник к фазе
падающей волны частоты
к единице, тем больше гармоник
задействовано в формировании отраженной
волны. Принципиальным моментом является
жесткая привязка фазы всех гармоник к фазе
падающей волны частоты ![]() .
В результате все гармоники складываются
синхронно, и отраженное поле имеет вид
коротких импульсов, следующих с частотой
.
В результате все гармоники складываются
синхронно, и отраженное поле имеет вид
коротких импульсов, следующих с частотой ![]() ,
с амплитудой, пропорциональной количеству
гармоник, и с длительностью, обратно
пропорциональной числу гармоник. Для
относительной комплексной амплитуды (2p+1)-ой
гармоники, подставляя в спектральное
разложение поля излучения (7) решения
уравнений движения (10) без инерционного
члена, можно получить следующее выражение:
,
с амплитудой, пропорциональной количеству
гармоник, и с длительностью, обратно
пропорциональной числу гармоник. Для
относительной комплексной амплитуды (2p+1)-ой
гармоники, подставляя в спектральное
разложение поля излучения (7) решения
уравнений движения (10) без инерционного
члена, можно получить следующее выражение:
![]()
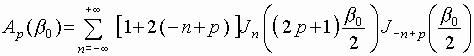
 ,
,
![]()
Анализ выражения (12) дает не только численное значение коэффициента преобразования мощности падающей волны в гармоники, но также показывает и сильную его зависимость от разности фаз колебаний электронного листа и волны.
3. Излучение листа в поле монохроматической волны.
Перейдем теперь к
самосогласованному анализу отраженного
поля в случае, когда движение листа
происходит под действием линейно-поляризованной
падающей волны ![]() .
Здесь, в отличие от случая, рассмотренного в
п. 2 будет учтена дисперсия электронной
среды, и, кроме того, существенно
негармонический характер электронных
осцилляций. Траекторию электронного листа
в этом случае можно представить как сумму
трех составляющих:
.
Здесь, в отличие от случая, рассмотренного в
п. 2 будет учтена дисперсия электронной
среды, и, кроме того, существенно
негармонический характер электронных
осцилляций. Траекторию электронного листа
в этом случае можно представить как сумму
трех составляющих:
При релятивистских
интенсивностях сила давления волны на лист
будет очень большой, что приведет к
быстрому продольному разгону до скорости,
близкой к световой, после чего лист
практически перестанет излучать назад (отражать).
Поэтому необходимо компенсировать среднюю
силу давления, для чего может быть
использовано, например, внешнее
статическое поле с напряженностью ![]() (в реальном эксперименте такое поле может
создаваться, например, положительным
зарядом тяжелых ионов). В самом деле, при
(в реальном эксперименте такое поле может
создаваться, например, положительным
зарядом тяжелых ионов). В самом деле, при![]() ,
где
,
где ![]() ,
сила
электростатического притяжения со стороны
ионного фона оказывается больше силы
светового давления, и в системе возможен
стационарный режим. При
,
сила
электростатического притяжения со стороны
ионного фона оказывается больше силы
светового давления, и в системе возможен
стационарный режим. При ![]() для полной компенсации силы давления
следует положить
для полной компенсации силы давления
следует положить ![]() [8]. В этом
случае уравнения движения (3)
электронного листа имеют вид:
[8]. В этом
случае уравнения движения (3)
электронного листа имеют вид:
где
Наиболее эффективное увеличение амплитуды отраженных импульсов и обогащение гармониками происходит согласно (3) при движении листа навстречу падающей волне со скоростью, близкой к
 ,
где множитель
,
где множитель Рис.3. Поле
излучения плазменного слоя в присутствии
раскачивающего поля при
а.)![]() и б.)
и б.)![]() .
.
4. Излучение листа в поле двух встречных волн.
Как уже отмечалось, для того, чтобы электронный лист совершал финитные колебания в поле мощной электромагнитной волны, необходимо компенсировать силу давления, которую оказывает волна на лист. В предыдущем разделе рассматривалась ситуация, в которой сила давления компенсировалась однородным электростатическим полем
Для напряженностей электрической и магнитной составляющих стоячей линейно-поляризованной волны имеем:
Уравнения движения (9) запишутся теперь в виде:
Здесь введены нормированные безразмерные переменные
Пусть сначала
В уравнении для
Без учета сил самодействия (радиационного трения) листа, описываемого последними членами в (16), уравнения (16) принадлежит к хорошо изученному типу уравнений движения частиц в высокочастотном поле. Классический результат
[9] состоит в том, что, в отсутствии радиационного трения продольное движение частиц представляет собой быстрые осцилляции на частотеПусть, например, выполнено условие
откуда для эффективной потенциальной энергии и эффективного коэффициента трения имеем выражения:
Первый член в (18) соответствует высокочастотному потенциалу Гапонова-Миллера, второй описывает влияние нелинейного радиационного трения. Можно показать, что при
Рис.4. Зависимость нормированной эффективной потенциальной энергии медленного дрейфа от продольной координаты для различных значений ускорительного параметра:
(1) - ![]() ;
(2) -
;
(2) - ![]()
Сравнивая для ![]() эффективную частоту колебаний вблизи
минимумов потенциальной энергии (18)
и затухание (19), можно сделать
вывод о том, что дрейф листа носит
характер апериодического сползания к
новому положению равновесия. Вследствие
того, что в новом положении равновесия
амплитуды электрического и магнитного
полей стоячей волны не равны нулю,
электронный лист совершает интенсивные
осцилляции на частоте
эффективную частоту колебаний вблизи
минимумов потенциальной энергии (18)
и затухание (19), можно сделать
вывод о том, что дрейф листа носит
характер апериодического сползания к
новому положению равновесия. Вследствие
того, что в новом положении равновесия
амплитуды электрического и магнитного
полей стоячей волны не равны нулю,
электронный лист совершает интенсивные
осцилляции на частоте ![]() в поперечном направлении и на частоте
в поперечном направлении и на частоте ![]() в продольном направлении, излучая при этом
электромагнитные волны. Таким образом,
эффективное излучение плазменного слоя в
поле стоячих волн возможно только для
достаточно мощных полей, обеспечивающих
в продольном направлении, излучая при этом
электромагнитные волны. Таким образом,
эффективное излучение плазменного слоя в
поле стоячих волн возможно только для
достаточно мощных полей, обеспечивающих ![]() (напомним, что аналитическое решение
получено при условии
(напомним, что аналитическое решение
получено при условии ![]() ).
Численный анализ полной системы уравнений
движения показывает, что при увеличении
амплитуды стоячей волны учет
релятивистских факторов в системе (15)
не изменяет качественно характер
продольного дрейфа. Для достаточно большой
амплитуды стоячей волны амплитуда
релятивистской скорости
).
Численный анализ полной системы уравнений
движения показывает, что при увеличении
амплитуды стоячей волны учет
релятивистских факторов в системе (15)
не изменяет качественно характер
продольного дрейфа. Для достаточно большой
амплитуды стоячей волны амплитуда
релятивистской скорости ![]() быстрых продольных ангармонических
осцилляций на частоте
быстрых продольных ангармонических
осцилляций на частоте ![]() стремится к единице, а излучение принимает
вид последовательности мощных импульсов,
следующих на двойной частоте волны. Форма
поля излучения представлена на рис. 5
и 6.
стремится к единице, а излучение принимает
вид последовательности мощных импульсов,
следующих на двойной частоте волны. Форма
поля излучения представлена на рис. 5
и 6.
Рис.5. Нестационарное
поле излучения плазменного слоя в
переходном режиме: ![]() ;
нормированная начальная координата слоя -
;
нормированная начальная координата слоя - ![]() .
.
Рис.6. Поле
излучения плазменного слоя в положительном
(а) и отрицательном (б) направлении оси ![]() при
при ![]() .
Движение происходит вблизи левого (относительно
узла электрической составляющей стоячей
волны) положения равновесия. Поле
излучения плазменного слоя в положительном
(а) и отрицательном (б) направлении оси
.
Движение происходит вблизи левого (относительно
узла электрической составляющей стоячей
волны) положения равновесия. Поле
излучения плазменного слоя в положительном
(а) и отрицательном (б) направлении оси ![]() при
при ![]() .
Движение происходит вблизи левого (относительно
узла электрической составляющей стоячей
волны) положения равновесия.
.
Движение происходит вблизи левого (относительно
узла электрической составляющей стоячей
волны) положения равновесия.
Существенным моментом является зависимость отраженного поля от начальных условий. Действительно, если начальное значение продольной координаты выбрано вблизи положения равновесия, то стационарное значение амплитуды поля излучения устанавливается практически в течение трех-пяти импульсов. Если же начальное значение координаты далеко от положения равновесия, то сначала излучаются один-два импульса с амплитудой больше стационарного значения (рис.5), затем следует длительный период, когда импульсы имеют относительно малую амплитуду, и далее устанавливается стационарный режим. Последний случай может быть интересен для проблемы генерации сверхширокополосных одиночных оптических импульсов.
Отметим еще один интересный
эффект, возникающий из-за наличия
бифуркации в рассматриваемой системе. При ![]() отражение волн становится несимметричным
относительно плазменного слоя (рис.
6). Дело в том, что в этом случае не только
процесс установления, но и вид
стационарного состояния становится
зависимым от начальных условий. На рис.
7 представлены стационарные траектории
электрона в ультрарелятивистском случае (
отражение волн становится несимметричным
относительно плазменного слоя (рис.
6). Дело в том, что в этом случае не только
процесс установления, но и вид
стационарного состояния становится
зависимым от начальных условий. На рис.
7 представлены стационарные траектории
электрона в ультрарелятивистском случае (![]() и
и
![]() )
при некотором определенном начальном
положении слоя. Асимметрия кривой
указывает на асимметрию при излучении в
положительном и отрицательном направлении
оси z и,
следовательно, при отражении волн. При
другом выборе начальных условий траектория
может быть зеркально отраженной
относительно узла электрической
составляющей стоячей волны.. Параметры
излучения слоя при этом меняются на
противоположные.
)
при некотором определенном начальном
положении слоя. Асимметрия кривой
указывает на асимметрию при излучении в
положительном и отрицательном направлении
оси z и,
следовательно, при отражении волн. При
другом выборе начальных условий траектория
может быть зеркально отраженной
относительно узла электрической
составляющей стоячей волны.. Параметры
излучения слоя при этом меняются на
противоположные.
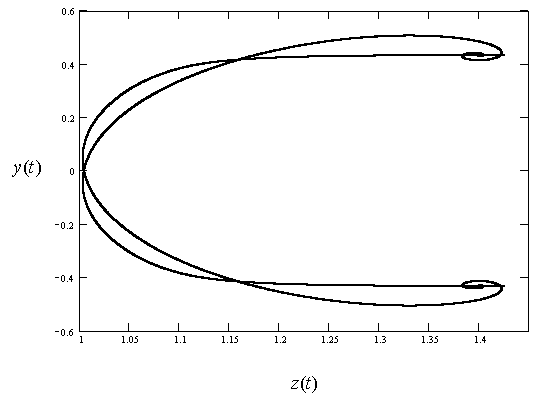
Рис.7. Стационарные
траектории движения плазменного слоя при ![]() (а) и
(а) и ![]() (б). Движение происходит вблизи левого
положения равновесия.
(б). Движение происходит вблизи левого
положения равновесия.
Обсуждение результатов.
Таким образом, при взаимодействии мощной электромагнитной волны с плотным плазменным слоем может генерироваться последовательность ультракоротких импульсов с амплитудой, значительно большей амплитуды падающей волны.
Оценим величину ускорительного параметра
Оценим возможную величину параметра
В настоящей работе рассмотрено перпендикулярное падение волны на плазменный лист. Полученные результаты легко могут быть обобщены на случай наклонного падения, используя прием, изложенный в [3]. Кроме того, прелагаемая методика позволяет находить не только отраженное поле, но также и прошедшую волну. Так, в [8] аналитически найдено выражение в третьем порядке по параметру
Для простоты и наглядности ионный фон не принимался во внимание при вышеприведенных расчетах. Однако, учесть влияние ионов можно с помощью подхода, использованного здесь для электронов. То же самое относится и к возможному начальному распределению электронов по скоростям - для каждого значения скорости необходимо вводить свой электронный лист с определенной поверхностной плотностью, а общую силу реакции излучения рассчитывать, интегрируя по функции распределения скоростей.
Физически реализовать модель тонкого плазменного листа можно, испаряя подвешенную тонкую (порядка нескольких микрон и менее) пленку мощным лазерным излучением. Видимо, эта задача наиболее естественно решается в поле двух стоячих волн. Следует отметить, что аналогом продольного низкочастотного качания листа, рассмотренного в п.3, является, по-видимому, случай, когда одна из встречных волн или обе являются модулированными.
В заключение отметим, что экспериментальное подтверждение возможности излучения электромагнитных импульсов может быть получено в интерферометрических экспериментах, например, использующих деление волнового фронта
[11], уже при умеренном значении мощности падающего излучения. Возможно также использование оптических нелинейностей в схеме, основанной на эффектах двухфотонной (многофотонной) люминесценции [12,13].Приложение.
В данном приложении будут обоснованы приведенные без доказательства в п.4 аналитические результаты о характере движения электронного листа в поле двух встречных волн.
Представим уравнения (16) в виде системы трех уравнений первого порядка:
(П.1)Введем следующий безразмерный параметр (в дальнейшем мы будем полагать его малым):
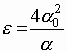
Тогда уравнения (П.1) представятся в виде:
Решение первого уравнения
системы (П.2) можно получить методом
последовательных приближений, представляя
поперечную скорость в виде ряда ![]() и
и
![]() приравнивая коэффициенты при одинаковых
степенях
приравнивая коэффициенты при одинаковых
степенях ![]() .
Далее нас будет интересовать решение с
точностью до
.
Далее нас будет интересовать решение с
точностью до ![]() .
.
Во втором слагаемом мы не стали
явно выписывать члены, порядка ![]() и
и 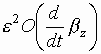 ,
т.к. в дальнейшем их можно будет отбросить.
,
т.к. в дальнейшем их можно будет отбросить.
Подставляя уравнение (П.3) в систему (П.2), получим два уравнения первого порядка:
П.4)Делая замену
Уравнения (П.5) будем решать методом усреднения
[14,15], для чего необходимо привести их к каноническому виду:Система (П.5) в новых переменных будет иметь вид:
(П.6)Производя теперь в (П.6) усреднение по времени, получим для дрейфовой составляющей продольной координаты следующее уравнение:
, (П.7)откуда непосредственно следует (17). Согласно теореме об усреднении
[15], ошибка при замене решенийСписок литературы:
Авторы:
Зиглин Сергей Львович,
Ильин Антон Сергеевич, asi@mail.cplire.ru
Кулагин Виктор Владимирович , kul@sai.msu.su
Черепенин Владимир Алексеевич, cher@mail.cplire.ru