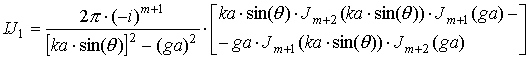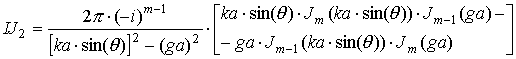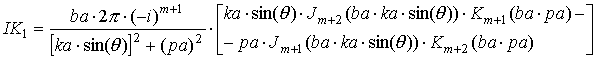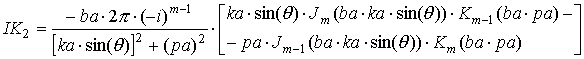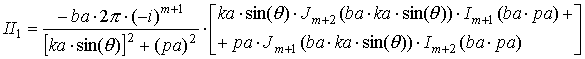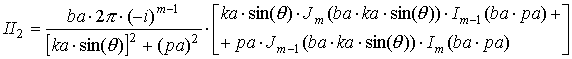| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2001 |
ОБ ИЗЛУЧЕНИИ ИЗ ОТКРЫТОГО КОНЦА КРУГЛОГО МЕТАЛЛОДИЭЛЕКТРИЧЕСКОГО ВОЛНОВОДА
Институт радиотехники и электроники РАН
Получена 13 февраля 2001 г.
В приближении Кирхгофа получены аналитические формулы для диаграммы направленности излучения из открытого конца круглого металлодиэлектрического волновода (экранированного диэлектрического волновода). Проведено численное исследование характеристик излучения, которое показало возможность реализации диаграмм направленности с низким уровнем боковых лепестков на двух поляризациях в широкой полосе частот, в том числе, осесимметричных диаграмм направленности.
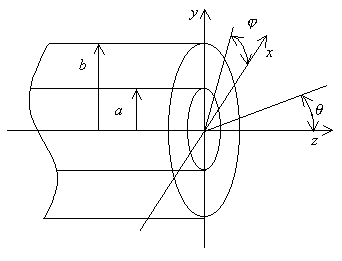
Рассмотрим
осесимметричный металлодиэлектрический волновод, представляющий собой
экранированный диэлектрический волновод (Рис.
1). Будем применять цилиндрическую
систему координат ![]() ,
, ![]() ,
, ![]() . Обозначим через
. Обозначим через ![]() и
и ![]() радиусы диэлектрического
волновода и экрана, через
радиусы диэлектрического
волновода и экрана, через ![]() ,
, ![]() - диэлектрические и
магнитные проницаемости диэлектрика.
- диэлектрические и
магнитные проницаемости диэлектрика.
Рис. 1. Металлодиэлектрический излучатель.
Закон
изменения составляющих поля вдоль оси ![]() положим в виде
положим в виде ![]() , где
, где ![]() - неизвестное пока
продольное волновое число. Для уменьшения числа параметров системы пронормируем
все размерные параметры (в том числе и длину волны в свободном пространстве
- неизвестное пока
продольное волновое число. Для уменьшения числа параметров системы пронормируем
все размерные параметры (в том числе и длину волны в свободном пространстве ![]() ) на радиус диэлектрического стержня
) на радиус диэлектрического стержня ![]() . Таким образом, введем следующие величины, которые будем
применять в дальнейших расчетах:
. Таким образом, введем следующие величины, которые будем
применять в дальнейших расчетах: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где – волновое число в свободном пространстве,
, где – волновое число в свободном пространстве, ![]() и
и ![]() – поперечные волновые
числа,
– поперечные волновые
числа, ![]() - радиус экрана.
- радиус экрана.
Собственные волны круглого
металлодиэлектрического волновода рассматривались в ряде работ (см., например,
[1]). Внутри диэлектрического стержня составляющие векторов электрического поля
![]() и магнитного поля
и магнитного поля ![]() можно представить в
виде:
можно представить в
виде:
|
|
|
а в воздушном слое:
|
|
|
где введены обозначения:
|
|
|
где ![]() - порядок
цилиндрических функций.
- порядок
цилиндрических функций.
Вид входящих в формулы функций и
параметров зависит от соотношений между длиной волны и параметрами волновода.
Условие ![]() выполняется всегда.
Однако при этом может быть как
выполняется всегда.
Однако при этом может быть как ![]() , так и
, так и ![]() . Волны, для которых
. Волны, для которых ![]() , называются "быстрыми", поскольку их длина волны
больше, чем длина плоской волны на той же частоте в аналогичной безграничной
среде, и, таким образом, фазовый фронт перемещается быстрее, чем фазовый фронт
плоской волны. Соответственно, волны, для которых
, называются "быстрыми", поскольку их длина волны
больше, чем длина плоской волны на той же частоте в аналогичной безграничной
среде, и, таким образом, фазовый фронт перемещается быстрее, чем фазовый фронт
плоской волны. Соответственно, волны, для которых ![]() , называются "медленными". Системы функций,
описывающих поперечные распределения амплитуд "быстрых" и
"медленных" волн различаются между собой.
, называются "медленными". Системы функций,
описывающих поперечные распределения амплитуд "быстрых" и
"медленных" волн различаются между собой.
Пусть для начала ![]() . Тогда поперечные волновые числа в диэлектрике и в воздухе
определяются по формулам:
. Тогда поперечные волновые числа в диэлектрике и в воздухе
определяются по формулам:
|
|
|
а входящие в выражения для полей функции:
|
|
|
|
|
|
Как можно легко заметить, для
аргумента, равного ![]() ,
, ![]() ,
, ![]() . Это обеспечивает обнуление тангенциальных составляющих
электрического поля
. Это обеспечивает обнуление тангенциальных составляющих
электрического поля ![]() и
и ![]() на металлическом экране.
на металлическом экране.
Уравнениям для полей удовлетворяют не все значения продольного волнового числа, а только те, для которых тангенциальные составляющие полей "сшиваются" на границе диэлектрического и воздушного слоев. Обозначим:
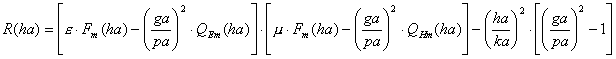 ,
,
|
|
|
Условие "сшивания" записывается с помощью характеристического уравнения [1]:
|
|
|
Решив это трансцендентное уравнение, получаем ряд дискретных значений продольного волнового числа, удовлетворяющих условиям сшивания полей на границе диэлектрика и воздуха, а также граничным условиям на металле.
Для случая ![]() поперечные волновые
числа в диэлектрике и в воздухе определяются по формулам:
поперечные волновые
числа в диэлектрике и в воздухе определяются по формулам:
|
|
|
а входящие в выражения для полей функции равны:
|
|
|
|
|
|
Функция ![]() для
характеристического уравнения
для
характеристического уравнения ![]() теперь будет такой:
теперь будет такой:
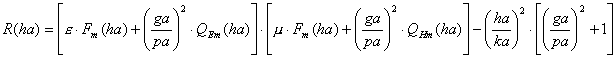 ,
,
а выражения для ![]() ,
, ![]() и
и ![]() останутся прежними с
учетом изменившихся функций
останутся прежними с
учетом изменившихся функций ![]() и
и ![]() .
.
Таким образом, системы волн в
двухслойном диэлектрическом волноводе для случаев ![]() и
и ![]() отличаются. Можно
показать, что если допустить возможность существования мнимого поперечного
волнового числа
отличаются. Можно
показать, что если допустить возможность существования мнимого поперечного
волнового числа ![]() , то два вышеуказанных случая будут переходить один в другой.
, то два вышеуказанных случая будут переходить один в другой.
Для анализа корней
характеристического уравнения можно использовать кривую зависимости ![]() при непрерывном
изменении продольного волнового числа. Исследуя эту кривую при определенных
геометрических и электрических параметрах волновода, можно определить
количество корней ,их приблизительные величины. и понять, как итерационная процедура находит решения
характеристического уравнения и на какие именно корни эта процедура выходит.
при непрерывном
изменении продольного волнового числа. Исследуя эту кривую при определенных
геометрических и электрических параметрах волновода, можно определить
количество корней ,их приблизительные величины. и понять, как итерационная процедура находит решения
характеристического уравнения и на какие именно корни эта процедура выходит.
Для вычисления диаграммы
направленности открытого конца металлодиэлектрического волновода в сферических
координатах ![]() ,
, ![]() ,
, ![]() , связанных с открытым концом волновода, выполним следующие
действия:
, связанных с открытым концом волновода, выполним следующие
действия:
1. Найдем векторы электрического и магнитного полей регулярного волновода в цилиндрических координатах.
2. Полагая в соответствии с приближением Кирхгофа, что поля на открытом конце волновода такие же, как и в регулярном волноводе, запишем интегральные представления для векторных потенциалов в дальней зоне.
3. Проинтегрируем выражения для векторных потенциалов в дальней зоне.
4. Найдем компоненты электрического и магнитного полей в дальней зоне.
Электрическое и магнитное поля выражаются через векторные потенциалы следующим образом [2]:
|
где векторные потенциалы определяются выражениями:
|
|
Связь между компонентами электрического и магнитного полей в цилиндрической (регулярный волновод) и декартовой (на торце волновода) системах координат определяется следующим образом:
|
|
|
Эти выражения подставляются в формулы для векторных потенциалов, после чего производится аналитическое интегрирование декартовых составляющих в дальней зоне. Затем производится переход к сферическим координатам.
Связь между тангенциальными (по отношению к апертуре, по которой проводится интегрирование) компонентами векторных потенциалов и их компонентами в сферической системе координат определяется формулами:
|
|
|
В дальней зоне компоненты электрического и магнитного полей поля выражаются через векторные потенциалы следующим образом:
|
|
|
Для получения конкретных выражений
снова сначала рассмотрим случай "быстрой" волны ![]() . После интегрирования по апертуре и перехода к сферическим
координатам получаем выражения для полей в дальней зоне:
. После интегрирования по апертуре и перехода к сферическим
координатам получаем выражения для полей в дальней зоне:
|
|
|
где выражения, входящие в формулы, определяются следующим образом:
|
|
Для
случая "медленной" волны ![]() получаем аналогичные
формулы:
получаем аналогичные
формулы:
|
|
|
где выражения, входящие в формулы, определяются следующим образом:
|
|
|
При выводе аналитических выражений использовались справочники [3-5].
Ограничимся рассмотрением мод
металлодиэлектрического волновода с косинусоидальной азимутальной зависимостью,
которые описываются цилиндрическими функциями первого порядка (![]() ). Исследование характеристического уравнения показало, что
для "медленных" волн (
). Исследование характеристического уравнения показало, что
для "медленных" волн (![]() ) изменение частоты слабо изменяет поперечное волновое число
внутри диэлектрика.
) изменение частоты слабо изменяет поперечное волновое число
внутри диэлектрика.
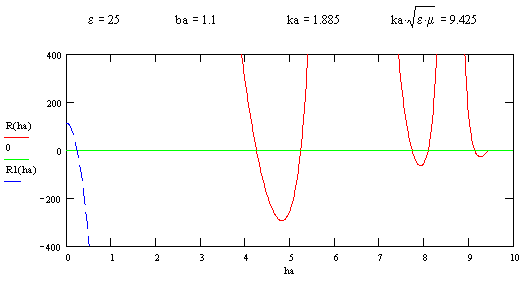
Рис. 2.
Кривые зависимости ![]() - для
"быстрой" волны:
- для
"быстрой" волны: ![]() и
и ![]() - для
"медленной" волны:
- для
"медленной" волны: ![]() .
.
На рисунке 2 изображены результаты
расчета кривых ![]() для случаев
для случаев ![]() (пунктирная линия) и
(пунктирная линия) и ![]() (сплошная линия).
Корни характеристического уравнения находятся на пересечениях кривых
(сплошная линия).
Корни характеристического уравнения находятся на пересечениях кривых ![]() с горизонтальной
осью. Из графика видно, что при
с горизонтальной
осью. Из графика видно, что при ![]() существует лишь один
корень, а при
существует лишь один
корень, а при ![]() - пять корней.
Следовательно, на одной частоте существуют шесть мод, и таким образом линия
работает в многомодовом режиме. Подбором геометрических и электрических
параметров системы можно добиться того, чтобы она работала в одномодовом
режиме, т.е. чтобы существовал лишь один корень, как показано на
рисунке 3.
Такой режим можно осуществить как для "быстрых", так и для
"медленных" волн.
- пять корней.
Следовательно, на одной частоте существуют шесть мод, и таким образом линия
работает в многомодовом режиме. Подбором геометрических и электрических
параметров системы можно добиться того, чтобы она работала в одномодовом
режиме, т.е. чтобы существовал лишь один корень, как показано на
рисунке 3.
Такой режим можно осуществить как для "быстрых", так и для
"медленных" волн.
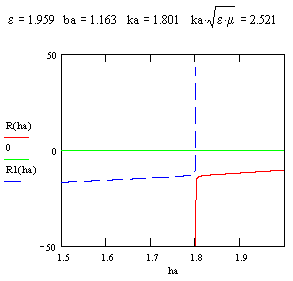
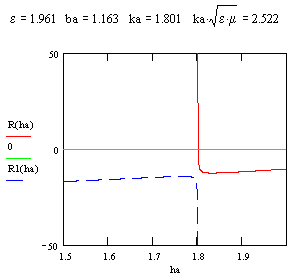
Рис. 3. Кривые
зависимости ![]() , иллюстрирующие смену модовых режимов в
металлодиэлектрическом волноводе в зависимости от изменения диэлектрической
проницаемости центрального стержня при фиксированной геометрии системы.
, иллюстрирующие смену модовых режимов в
металлодиэлектрическом волноводе в зависимости от изменения диэлектрической
проницаемости центрального стержня при фиксированной геометрии системы.
На
рисунке 3 показано, как в
металлодиэлектрическом волноводе при изменении диэлектрической проницаемости
центрального стержня от ![]() 1,959 (а) до
1,959 (а) до ![]() 1,961 (б) возле точки
1,961 (б) возле точки ![]() происходит переход от
модового режима "быстрой" волны
происходит переход от
модового режима "быстрой" волны ![]() к режиму
"медленной" волны
к режиму
"медленной" волны ![]() .
.
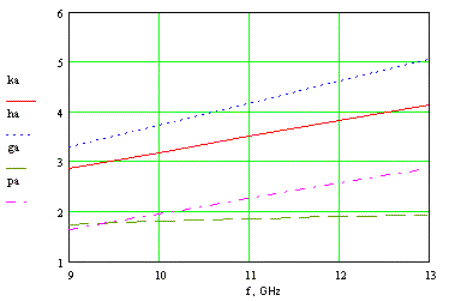
Рис. 4. Частотная зависимость волновых чисел.
На рисунке 4 показана зависимость волновых чисел от частоты. Поскольку слабее всего меняется поперечное волновое число в диэлектрике, а именно оно определяет вид диаграммы направленности, можно предположить, что диаграмма направленности также слабо меняется от частоты.
а) Частота 9 ГГц.
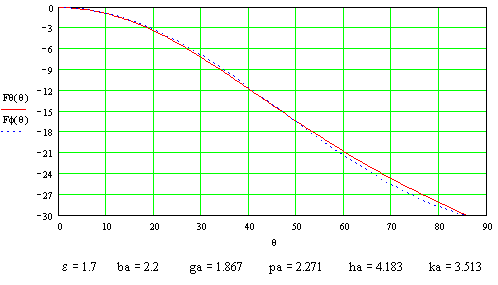
б) Частота 11 ГГц.
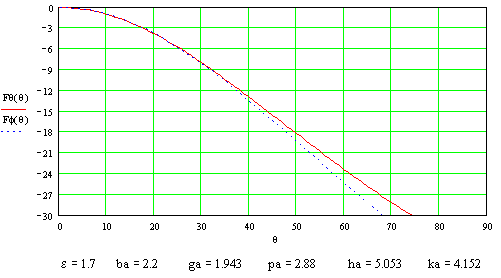
в) Частота 13 ГГц.
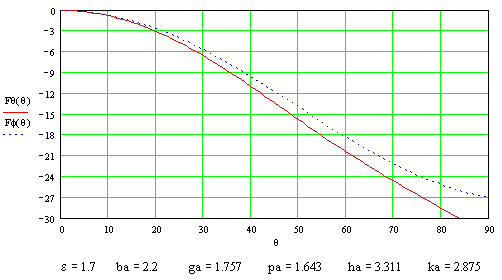
Рис. 5. Диаграммы направленности металлодиэлектрического волновода.
На
рисунке 5 изображены диаграммы
направленности (в Дб) металлодиэлектрического волновода в плоскости ![]() при
при ![]() (
(![]() -плоскость) и перпендикулярной к ней плоскости
-плоскость) и перпендикулярной к ней плоскости ![]() при
при ![]() (
(![]() -плоскость). Расчет проводился при частотах 9, 11 и 13 ГГц
для металлодиэлектрического волновода с радиусом диэлектрического стержня
-плоскость). Расчет проводился при частотах 9, 11 и 13 ГГц
для металлодиэлектрического волновода с радиусом диэлектрического стержня ![]() =15,25 мм. Остальные
электрические и геометрические параметры волновода (указанные в подрисуночной
подписи) подобраны таким образом, чтобы диаграммы направленности в
=15,25 мм. Остальные
электрические и геометрические параметры волновода (указанные в подрисуночной
подписи) подобраны таким образом, чтобы диаграммы направленности в ![]() - и
- и ![]() - плоскостях имели
хорошее совпадение в широком диапазоне углов. Из рисунка видно, что диаграммы
направленности слабо меняются при изменении частоты. Это объясняется тем, что
поле сосредоточено в основном внутри диэлектрика, снаружи оно экспоненциально затухает
от границы "диэлектрик - воздух" до металлической стенки, а поперечное
волновое число внутри диэлектрика, как уже отмечалось выше, слабо зависит от
частоты.
- плоскостях имели
хорошее совпадение в широком диапазоне углов. Из рисунка видно, что диаграммы
направленности слабо меняются при изменении частоты. Это объясняется тем, что
поле сосредоточено в основном внутри диэлектрика, снаружи оно экспоненциально затухает
от границы "диэлектрик - воздух" до металлической стенки, а поперечное
волновое число внутри диэлектрика, как уже отмечалось выше, слабо зависит от
частоты.
Таким образом, проведенные исследования показали перспективность использования излучателей в виде открытого конца круглого металлодиэлектрического волновода в качестве широкополосных облучателей зеркальных и линзовых антенн. Такие излучатели позволяют реализовать диаграммы направленности с низким уровнем боковых лепестков на двух поляризациях в широкой полосе частот, в том числе осесимметричные диаграммы направленности.
ЛИТЕРАТУРА
1. Г.И. Веселов, Л.А. Любимов К теории двухслойного диэлектрического волновода в цилиндрическом экране, Радиотехника и электроника, т.8, №9, 1963, стр. 1530-1541.
2. Л.А. Вайнштейн Электромагнитные волны, М., Радио и связь, 1988.
3. М. Абрамовиц, И. Стиган Справочник по специальным функциям, М., Наука, 1979.
4. А.П. Прудников, Ю.А. Брычков, О.И. Маричев Интегралы и ряды. Специальные функции, М., Наука, 1983.
5. И.С. Градштейн, И.М. Рыжик Таблицы интегралов, сумм, рядов и произведений, М., Государственное издательство физико - математической литературы, 1962.
Авторы:
д.ф.-м.н. Вадим Анатольевич Калошин, email: vak@cplire.ru
к.ф.-м.н. Михаил Весник, email: vesnik@cplire.ru
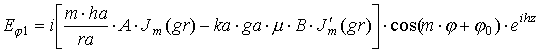
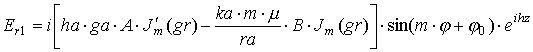
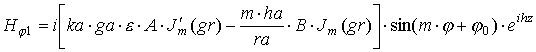
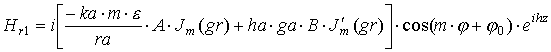
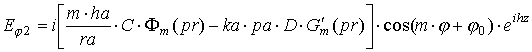
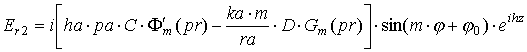
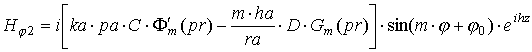
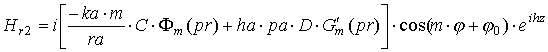
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
, 
 ,
, 
 .
. ,
, 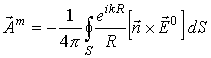
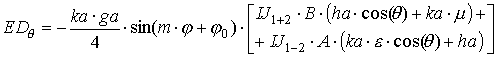
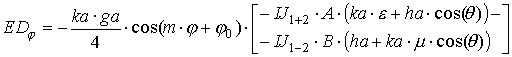
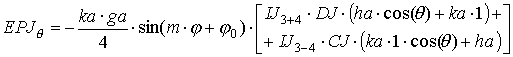
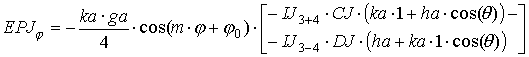
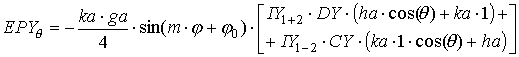
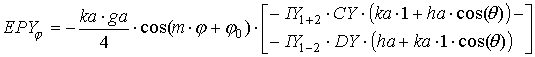
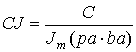 ,
,  ,
,  ,
,  .
.
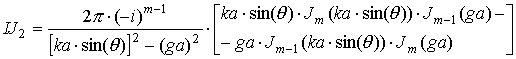
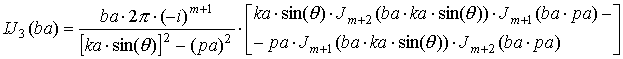
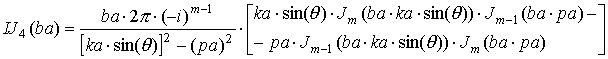
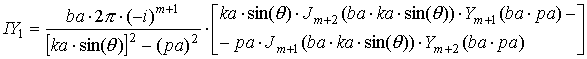
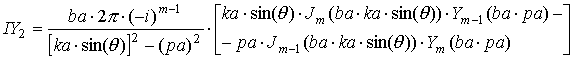
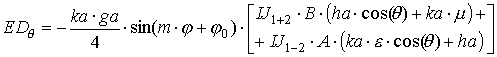
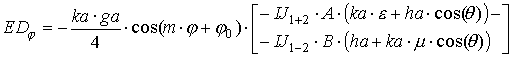
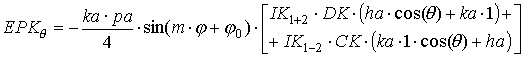
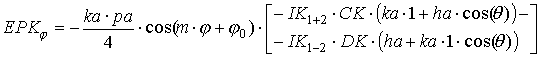
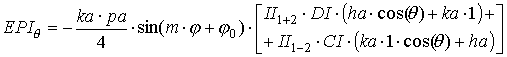
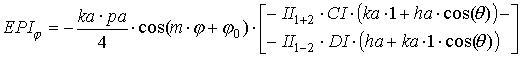
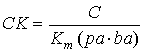 ,
,  ,
,  ,
,  ,
,