|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2002 |
|
ЭЛЕКТРОННОЕ «УЗКОЕ ГОРЛО» И АНОМАЛИИ ЗАТУХАНИЯ КВАНТОВАНИЯ ЛАНДАУ.
В.И. Кадушкин, А.Б. Дюбуа.
E-mail: kadush@ttc.ryazan.ru
Рязанский государственный педагогический университет.
Получена 10 мая 2002 г.
Найдены выражения для времени электрон – электронной релаксации, матричных элементов потенциала полной экранировки и динамической зависимости диэлектрической функции 2D – электронной системе с тонкой структурой энергетического спектра и пространственного распределения электронной плотности. Результаты расчетов хорошо описывают осциллирующую зависимость времени столкновительного уширения уровней Ландау от температуры. Показана доминирующая роль в электрон – электронных столкновениях одного из сателлитов электронов возбужденной подзоны размерного квантования. Исследован спектр плазмонов.
1. Электрон - электронные взаимодействия играют первостепенную роль в кинетических явлениях. Среди других следует отметить эффекты горячих электронов, квантовые поправки к проводимости, и затухание квантования Ландау в объемных и двумерных полупроводниковых соединениях с вырожденными электронами. Известны аномалии низкотемпературного магнитотранспорта, связанные с заполнением 2D электронами нескольких подзон размерного квантования [1-3].
В [4] обнаружена
осциллирующая зависимость времени нетеплового (столкновительного) уширения
уровней Ландау от температуры и концентрации 2D вырожденных электронов ![]() . Там же предложена качественная
интерпретация наблюдаемым эффектам на основе учета конкуренции каналов электрон
- электронных («е-е») взаимодействий в сложной электронной системе. Попытки
привлечь результаты работ [5,6] к количественному описанию экспериментов
[4]
окончились неудачей, так как рассматриваемые теорией модели не соответствовали
реальной экспериментальной ситуации [4] (учета
. Там же предложена качественная
интерпретация наблюдаемым эффектам на основе учета конкуренции каналов электрон
- электронных («е-е») взаимодействий в сложной электронной системе. Попытки
привлечь результаты работ [5,6] к количественному описанию экспериментов
[4]
окончились неудачей, так как рассматриваемые теорией модели не соответствовали
реальной экспериментальной ситуации [4] (учета ![]() и динамической зависимости диэлектрической
функции).
и динамической зависимости диэлектрической
функции).
В настоящей работе
сообщаются результаты исследований «е-е» релаксационных процессов в системе
сильновырожденных 2D электронов с
тонкой структурой энергетического спектра и пространственного распределения
электронной плотности. Найдены выражения для времени «е-е» внутри - ![]() и межподзонного
и межподзонного ![]() взаимодействия,
определены матричные элементы полного потенциала экранирования и диэлектрической функции
взаимодействия,
определены матричные элементы полного потенциала экранирования и диэлектрической функции ![]() в условиях
в условиях ![]() и приближении далекого от длинноволнового
предела. Показано, что осцилляции
и приближении далекого от длинноволнового
предела. Показано, что осцилляции ![]() связаны с возбуждением плазменных
колебаний компонентов 2D
электронной системы. Исследован спектр частот плазмонов.
связаны с возбуждением плазменных
колебаний компонентов 2D
электронной системы. Исследован спектр частот плазмонов.
Рассмотрение «е-е» взаимодействия
выполнено на основе расчета энергетической структуры зоны проводимости ![]() (см. рис. 7 в
[4]).
Потенциальную яму гетероперехода,
(см. рис. 7 в
[4]).
Потенциальную яму гетероперехода,
![]() подобно [7], аппроксимируем треугольным
профилем с изломами на уровнях размерного квантования
подобно [7], аппроксимируем треугольным
профилем с изломами на уровнях размерного квантования ![]() и
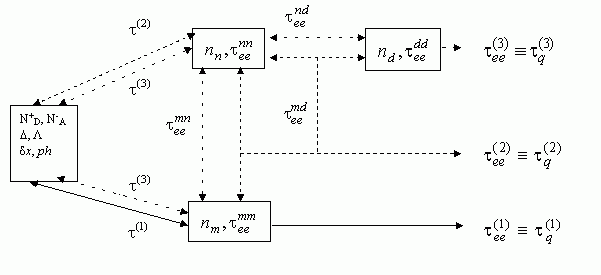
и ![]() . Схема-модель «е-е» взаимодействий в 2D электронной системе представлена на
рис. 1, где также приведены типичные каналы прохождения возмущения от
источников (ионизированные доноры
. Схема-модель «е-е» взаимодействий в 2D электронной системе представлена на
рис. 1, где также приведены типичные каналы прохождения возмущения от
источников (ионизированные доноры ![]() , акцепторы
, акцепторы ![]() , островки роста длиной Λ и высотой
Δ, колебания мольной доли δх). Здесь введены обозначения:
, островки роста длиной Λ и высотой
Δ, колебания мольной доли δх). Здесь введены обозначения: ![]() – концентрация 2D электронов основной подзоны
размерного квантования (main –
компонент), а
– концентрация 2D электронов основной подзоны
размерного квантования (main –
компонент), а ![]() ,
,
![]() - ближний (near) и удаленный (distance) от гетерограницы сателлиты возбужденного
компонента (perturbed – компонент)
- ближний (near) и удаленный (distance) от гетерограницы сателлиты возбужденного
компонента (perturbed – компонент) ![]() (в дальнейшем n и d сателлиты) возбужденной подзоны
размерного квантования. Из всей совокупности нами рассмотренных каналов
разрушения квантования Ландау следует выделить три, на которых просматриваются
основные особенности. Поскольку
(в дальнейшем n и d сателлиты) возбужденной подзоны
размерного квантования. Из всей совокупности нами рассмотренных каналов
разрушения квантования Ландау следует выделить три, на которых просматриваются
основные особенности. Поскольку ![]() и «центры тяжести»
и «центры тяжести» ![]() на уровнях
на уровнях ![]() и
и ![]() пространственно разнесены, то
возмущение от источника за
пространственно разнесены, то
возмущение от источника за
![]() воспринимает массив
воспринимает массив ![]() 2D электронов. За счет внутриподзонного (
2D электронов. За счет внутриподзонного (![]() ) и межподзонных (
) и межподзонных (![]() ) «е-е» взаимодействий,
опосредованных
) «е-е» взаимодействий,
опосредованных ![]() и
и
![]() внутриподзонным
взаимодействием, возмущение распространяется на всю 2D электронную систему. Траектория этого механизма на
рис. 1
показана сплошной линией:
внутриподзонным
взаимодействием, возмущение распространяется на всю 2D электронную систему. Траектория этого механизма на
рис. 1
показана сплошной линией:
Рис. 1
Схема — модель каналов прохождения возмущения от источников формирующих нетепловое, столкновительное уширение уровней Ландау. Пояснения в тексте.
Определяющим фактором
здесь является взаимодействие ![]() и
и ![]() электронов: «m-d», а
электронов: «m-d», а ![]() - есть пассивный («n») элемент. Второй сценарий соответствует восприятию
возмущения n – сателлитом. В этом случае время
разрушения формируется в цепочке, показанной на рис.1 штриховой линией; так
- есть пассивный («n») элемент. Второй сценарий соответствует восприятию
возмущения n – сателлитом. В этом случае время
разрушения формируется в цепочке, показанной на рис.1 штриховой линией; так
Контролирующими ситуацию факторами
являются межподзонное взаимодействие «n-d», «n-m», «m-d». Взаимодействие «n-d» - основное в этом канале, а ![]() – пассивный элемент. Третий
вариант формируется в цепочке, где основным взаимодействием является «m-n»,
– пассивный элемент. Третий
вариант формируется в цепочке, где основным взаимодействием является «m-n», ![]() - есть пассивный элемент:
- есть пассивный элемент:
Траектория показана штрихпунктирной линией.
По характеру переходов «е-е» взаимодействий можно разделить на три типа: 1 – взаимодействия в одной подзоне, ограниченное переходами в пределах этой подзоны; 2 – внутриподзонное взаимодействие, возбуждающее межподзонные переходы; 3 – взаимодействие электронов различных подзон, вызывающее также и внутриподзонную реакцию.
2. Время е-е взаимодействия,
за которое состояние ![]() переходит
в
переходит
в ![]() с точностью до второго члена разложения внешнего
потенциала
с точностью до второго члена разложения внешнего
потенциала ![]() теории
возмущения определяется известным соотношением
теории
возмущения определяется известным соотношением
где комбинация индексов i, j, k, l пробегают совокупность m (основной компонент), n, d (саттелиты ![]() - компонента), которые описывают тип
электронных переходов. Используя тождественные преобразования [8], перепишем
(4) в виде
- компонента), которые описывают тип
электронных переходов. Используя тождественные преобразования [8], перепишем
(4) в виде
где
где ![]() , S- площадь 2D электронного газа.
, S- площадь 2D электронного газа.
Матричные элементы потенциала полной экранировки с учетом параметров энергетической диаграммы для первого и второго типов переходов приводятся к виду
для i=k и j=l, а для третьего типа
с i=j и k=l.
Времена релаксации в виде удобном для вычислений для 1-го и 2-го типов переходов имеют вид функций
а для 3- го типа
при i≠1, где P-n(T), Q-n(T), W-n(T)многочлен степени «-n»,. ζ – дзета-функция Римана.
Расчеты ![]() выполнены в
соответствии со схемой-моделью каналов разрушения квантования Ландау. При этом,
учитывая «траектории» каналов (1)-(3), включающие как внутри-, так и межподзонные переходы, расчет
выполнены в
соответствии со схемой-моделью каналов разрушения квантования Ландау. При этом,
учитывая «траектории» каналов (1)-(3), включающие как внутри-, так и межподзонные переходы, расчет ![]() нами выполнен по формулам (9) и (10), в
соответствии со следствием правила Матиссена
нами выполнен по формулам (9) и (10), в
соответствии со следствием правила Матиссена ![]() , где суммирование выполняется по всем
внутри- и межподзонным компонентам схемы-модели (рис. 1).
, где суммирование выполняется по всем
внутри- и межподзонным компонентам схемы-модели (рис. 1).
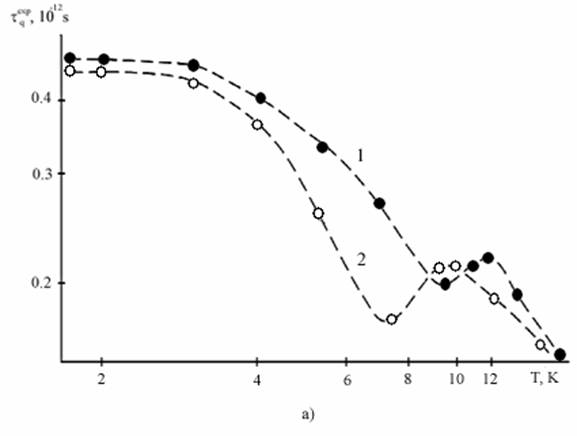
На рис. 2а и 2б приведены
экспериментальные и расчетные зависимости времени разрушения квантования Ландау
для двух гетероструктур с концентрацией, достаточной для заполнения двух подзон
размерного квантования (детали обработки эксперимента в [4]). Первое, на что
следует обратить внимание, это количественное «попадание» расчетов в интервал
величин τ в изученной области температур 2≤Т≤12К для реальных концентраций ![]() ,
, ![]() ,
, ![]() и, соответственно,
и, соответственно, ![]() . Из всех рассмотренных
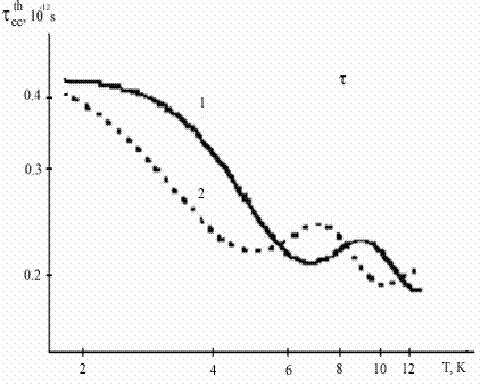
вариантов схемы-модели (рис. 1) наиболее удовлетворителен сценарий (3). Именно
для него и представлены результаты расчета
. Из всех рассмотренных
вариантов схемы-модели (рис. 1) наиболее удовлетворителен сценарий (3). Именно
для него и представлены результаты расчета ![]() на рис. 2б.
на рис. 2б.
б)
Рис. 2
Сопоставление
экспериментальных
![]() (из
работы [4])— (а) и расчетных
(из
работы [4])— (а) и расчетных
![]() —(b) зависимостей:
—(b) зависимостей:
![]() , 1011
см-2: 1—9.1, 2—10.
, 1011
см-2: 1—9.1, 2—10.
При низких температурах (Т<5К) затухание квантования Ландау
определяется ![]() электронами.
Численный анализ разложения диэлектрических функций (6) показывает появление немонотонностей
электронами.
Численный анализ разложения диэлектрических функций (6) показывает появление немонотонностей
![]() при
при ![]() и Т>5К. Это позволяет утверждать, что характерные осцилляции
и Т>5К. Это позволяет утверждать, что характерные осцилляции ![]() появляются лишь с
заполнением электронами второй возбужденной подзоны размерного квантования и
отклика на температурное воздействие при Т>5К. Второй результат – это роль в
возникновении осцилляций
появляются лишь с
заполнением электронами второй возбужденной подзоны размерного квантования и
отклика на температурное воздействие при Т>5К. Второй результат – это роль в
возникновении осцилляций ![]() - сателлита, независимо от того какой
компонент 2D электронов воспринимает возмущение. Это
на рис. 1 показано каналом
- сателлита, независимо от того какой
компонент 2D электронов воспринимает возмущение. Это
на рис. 1 показано каналом ![]() . Напрямую это видно, если положить
. Напрямую это видно, если положить ![]() , отличными от нуля
будут лишь
, отличными от нуля
будут лишь ![]() и
и ![]() и осцилляций
и осцилляций ![]() не возникает.
не возникает.
Эффект электронного
«узкого горла» состоит в следующем. Изменение (повышение) температуры опыта инициирует
сканирование внешнего возмущения ![]() по частоте в сторону увеличения
ω. 2D система электронов «прозрачная» для
по частоте в сторону увеличения
ω. 2D система электронов «прозрачная» для ![]() до того момента, пока не будет достигнута
до того момента, пока не будет достигнута ![]() одного из компонентов.
Наименьшая
одного из компонентов.
Наименьшая ![]() соответствует
соответствует
![]() сателлиту.
Этот компонент, а именно внутриподзонная релаксация его и является «узким
горлом» для
сателлиту.
Этот компонент, а именно внутриподзонная релаксация его и является «узким
горлом» для ![]() ,
возбуждающим 2D систему электронов в целом. Что, в
конечно счете, разрушает квантование циклотронных орбит (затухание квантования
Ландау). Этот эффект «узкого горла» иллюстрирует совпадение резонансных частот
для «m-n» и «d-n» каналов (см. ниже на рис. 4 (кривые 1 и 3) в области
низких частот).
,
возбуждающим 2D систему электронов в целом. Что, в
конечно счете, разрушает квантование циклотронных орбит (затухание квантования
Ландау). Этот эффект «узкого горла» иллюстрирует совпадение резонансных частот
для «m-n» и «d-n» каналов (см. ниже на рис. 4 (кривые 1 и 3) в области
низких частот).
Таким образом, экспериментально
наблюдаемые особенности ![]() для области Т<5К связаны только с
внутризонными «е-е» переходами
для области Т<5К связаны только с
внутризонными «е-е» переходами ![]() ≈
≈![]() ≈
≈![]() . При более высоких температурах
реализуется смешанный механизм разрушения квантования Ландау:
. При более высоких температурах
реализуется смешанный механизм разрушения квантования Ландау: ![]() .
.
Необходимо отметить, что, варьируя
параметры ямы, можно добиться удовлетворительного согласия с экспериментом.
Данная методика открывает возможность воссоздания реального профиля потенциала
по суперпозиции зависимостей ![]() и
и ![]() для образцов различной степени легирования
и соответственно отличающих вариацией формфакторов
для образцов различной степени легирования
и соответственно отличающих вариацией формфакторов ![]() и
и ![]() . Однако такое
совмещение расчетных кривых
. Однако такое
совмещение расчетных кривых ![]() с экспериментальными
с экспериментальными ![]() ограничено определенным
произволом в подгоночных параметрах
ограничено определенным
произволом в подгоночных параметрах ![]() и
и ![]() — формфакторах потенциальной
ямы. Последнее связано с тем, что вид Ec(z) может быть установлен с достаточным приближением, это
касается величин ND, NA,
неоднозначности разрыва зон
— формфакторах потенциальной
ямы. Последнее связано с тем, что вид Ec(z) может быть установлен с достаточным приближением, это
касается величин ND, NA,
неоднозначности разрыва зон ![]() для AlGaAs/GaAs
гетеросистемы (см. например [9] и [10]).
для AlGaAs/GaAs
гетеросистемы (см. например [9] и [10]).
3. Естественными (исходя из осцилляций ![]() и
и ![]() ) представляются соображения о резонансном
отклике компонентов сложной 2D
электронной системы на внешнее возмущение
) представляются соображения о резонансном
отклике компонентов сложной 2D
электронной системы на внешнее возмущение ![]() на частоте плазменных колебаний. На спектр
на частоте плазменных колебаний. На спектр ![]() электронная 2D
система реагирует одним из
электронная 2D
система реагирует одним из ![]() компонентов (или их комбинацией), и
за время tee(
компонентов (или их комбинацией), и
за время tee(![]() ) возмущение распространяется на всю систему. Это приводит к
разрушению квантовых состояний (циклотронных орбит), что в эксперименте сопровождается
уменьшением амплитуды осцилляций d(1/В)Т. Последнее формально эквивалентно повышению
температуры опыта Т. Поэтому резонансному отклику с разрушением квантования
Ландау соответствует минимум на зависимостях
) возмущение распространяется на всю систему. Это приводит к
разрушению квантовых состояний (циклотронных орбит), что в эксперименте сопровождается
уменьшением амплитуды осцилляций d(1/В)Т. Последнее формально эквивалентно повышению
температуры опыта Т. Поэтому резонансному отклику с разрушением квантования
Ландау соответствует минимум на зависимостях ![]() и
и ![]() .
.
Нами
выполнен спектральный анализ дисперсионных уравнений для ![]() (6) для различных каналов «е-е» взаимодействий
согласно схемы рис.1 и различных соотношений концентраций
(6) для различных каналов «е-е» взаимодействий
согласно схемы рис.1 и различных соотношений концентраций ![]() при условии заполнения двух подзон размерного
квантования (
при условии заполнения двух подзон размерного
квантования (![]() ).
Условие существования плазменных колебаний на частоте
).
Условие существования плазменных колебаний на частоте ![]() определяется дисперсионным
уравнением
определяется дисперсионным
уравнением ![]() . При этом минимумам
. При этом минимумам ![]() соответствуют минимум
соответствуют минимум ![]() и
и ![]() , а максимуму на
, а максимуму на ![]() соответствуют
соответствуют ![]() и максимум
и максимум ![]() [5,11].
[5,11].
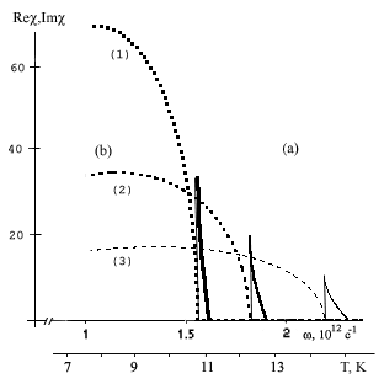
На рис.3 и
4
иллюстрируется соотносительность парциальных вкладов отдельных механизмов в
формирование разрушения квантования Ландау и концентрационные особенности. Так
на рис.3 приведены частотные зависимости ![]() и
и ![]() для
для ![]() трех каналов межподзонных переходов.
Видно, что доминирующим является взаимодействия
трех каналов межподзонных переходов.
Видно, что доминирующим является взаимодействия ![]() и
и ![]() . Более того, резонансная частота
определяется концентрацией n-сателлита.
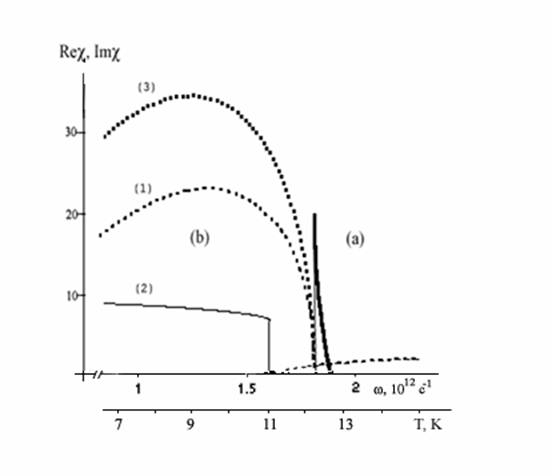
На рис.4 показано влияние степени заполнения второй подзоны размерного квантования.
С увеличением концентрации
. Более того, резонансная частота
определяется концентрацией n-сателлита.
На рис.4 показано влияние степени заполнения второй подзоны размерного квантования.
С увеличением концентрации ![]() , а следовательно, и
, а следовательно, и ![]() (и
(и ![]() , соответственно), резонансная
частота смещается на область больших величин, а контрастность разрыва
, соответственно), резонансная
частота смещается на область больших величин, а контрастность разрыва ![]() и
и ![]() уменьшается. ( это все соответствует третьему сценарию схемы-модели
рис.1).
уменьшается. ( это все соответствует третьему сценарию схемы-модели
рис.1).
Рис. 3.
Частотная зависимость диэлектрической функции для взаимодействия основной подзоны размерного квантования с «n—сателлитом». nm,1011 см-2: (1) — 8.5, (2) — 10, (3) — 11.5. dp/dm=3.5.
Рис. 4
Частотная зависимость диэлектрической функции для концентрации nm=10·1011 см-2. (1) – «d — n взаимодействие», (2) — «m — d взаимодействие», (3) — «m — n взаимодействие». dp/dm=3.5.
Аналогичные исследования для других каналов по траекториям (1) и (2) схемы-модели рис.1 в целом подтвердили тенденции результатов, представленные на рис.3 и 4.
Работа выполнена при частичной финансовой поддержке Минпром науки и технологий РФ (грант 4.15.99) Программы АНФКС и гранта № Е 00-3.4-75 Минобразования РФ.
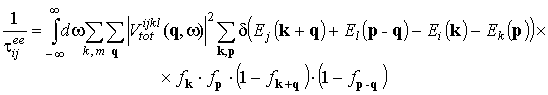 , (4)
, (4)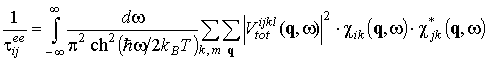 , (5)
, (5)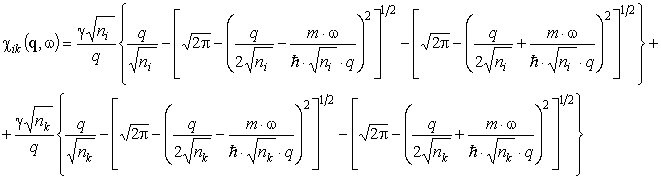 , (6)
, (6)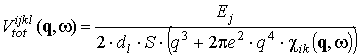 (7)
(7)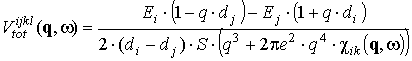 (8)
(8)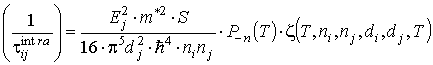 (9)
(9)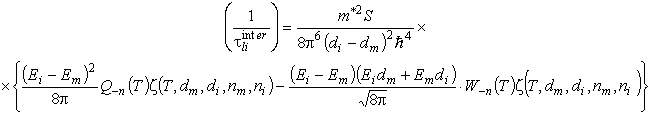 , (10)
, (10)