|
|
"JOURNAL OF RADIOELECTRONICS" N 10, 2002 |
|
DISCRETE WAVELET TRANSFORM APPLICATION TO RAYLEIGHT FADING CHANNEL ESTIMATION IN RADIO COMMUNICATIONS
Zaharov V.V., Fausto Casco S.
Universidad Autonoma Metropolitana - Iztapalapa,
México D.F., MEXICO,
Tel. (5255)55923957, vick@xanum.uam.mx
Received on 20.09.2002.
Four algorithms for flat fading radio channel estimation was investigated, namely algorithms based on AR-model with sliding window and without sliding window, algorithm that uses Discrete Wavelet Transform, algorithm that uses Discrete Wavelet Packet Transform. As it is shown, the application of DWT and DWPT in channel estimation problem allows decrease the square average prediction error in comparison with methods that use AR-model. It is shown as well that performance of the radio communications with application DWT and DWPT can be increase the capacity of the channel up to ~3 dB comparing with conventional method based on AR-model. This goal obtained due to more detailed analysis of flat fading channel in the varied bands of frequency that received from coefficients of DWT and DWPT.
Within the past few years Discrete Wavelet Transforms (DWT) have received considerable attention in the technical literature, prompting applications in a variety of disciplines such a speech and image processing, compression, signal processing, information theory etc.[1-4,8,9,11], because it allows to present investigated process more adequately.
The basis of complex exponents used in Discrete Fourier Transform (DFT) is optimal as to the many criteria in case of stationary process since whereat the coefficients of decomposition are uncorrelated. In case of nonstationary process they lose localization in time domain. The analysis of such signals is possible with the DFT using sliding window through the data [6,7]. The disadvantage of such approach is the high computational complexity of the decomposition algorithm.
In DWT instead of harmonic orthogonal functions are used the systems of functions generated by shifts and the compressions of some generating functions with compact support in frequency and time domains. That allows divide process on “small details” in frequency domain and in the same time to localize them in time domain. This "compact support" allows the wavelet transform to translate a time-domain function into a representation that is not only localized in frequency but in time as well.
Fundamentally,
wavelets are a new type of function, which provide an excellent orthonormal
basis for functions of one or more variables. They provide a localized basis,
and can represent any square-integrable functions in a locally finite manner.
In [4] was fined for the first time a parameterised family of orthonormal
systems of functions in ![]() with certain important complementary
properties:
with certain important complementary
properties:
·
Each system is
generated from a scaling function and a wavelet function by rescaling and
translations, and the
wavelet system is an orthonormal basis for ![]() .
.
· Each element in a given system has compact support in time and frequency domain.
· There are fast algorithms for computing the coefficients of wavelet transform
The first application of DWT for linear prediction system was proposed in [3]. The concept behind this system is to use the DWT to decompose the data into "subspaces" that are easier to model with multiple linear predictors. The paper [12] considers the DWT application for market stock rate analysis some of the nonstationary data. In [5] the Autoregressive Model (AR) was described for prediction of the fading channel with slow sampling rate using minimum mean square error criteria.
In this paper four algorithms for flat fading radio channel estimation will be investigated: two algorithms based on AR-model, algorithm that based on Discrete Wavelet Transform (DWT) and algorithm that based on Discrete Wavelet Packet Transform (DWPT). The comparative analysis of algorithm by criteria of mean square average prediction error and probability of bit error rate was carried out as well.
2. RAYLEIGHT FADING CHANNEL DESCRIPTION
The fading signal is result of the interference between several scattered signals. One the method of decreasing of influence of the fading signal on signal of interest is based on prediction of future fading by estimation of important scatters, e.g. their relative phases, directions and amplitudes. We consider a low-pass complex model of the received signal [10]
where ![]() is
the multiplicative flat fading coefficients,
is
the multiplicative flat fading coefficients, ![]() is the transmitted signal, and
is the transmitted signal, and ![]() is additive white
Gaussian noise (AWGN), M is number of scatters,
is additive white
Gaussian noise (AWGN), M is number of scatters, ![]() is the amplitude, Doppler
frequency and phase on the n-th scatters,
is the amplitude, Doppler
frequency and phase on the n-th scatters, ![]() is data sequence,
is data sequence, ![]() is the transmitter pulse, and
is the transmitter pulse, and ![]() is symbol duration.
is symbol duration.
Output of the discrete - time system is given by
where ![]() is
sampled the fading signal and
is
sampled the fading signal and ![]() is discrete AWGN process.
is discrete AWGN process.
As shown in [10] ![]() can be modeled as
complex Gaussian random process with Rayleight distributed amplitudes and
uniform phases. In a variety of mobile radio environments the multipath signal
consists of about 10 or fewer discrete sinusoidal components, that changes
their parameters
can be modeled as
complex Gaussian random process with Rayleight distributed amplitudes and
uniform phases. In a variety of mobile radio environments the multipath signal
consists of about 10 or fewer discrete sinusoidal components, that changes
their parameters ![]() much
slower that the coherent time of the signal envelope. Thus, the fading
coefficients can be predicted for beyond the coherence time.
much
slower that the coherent time of the signal envelope. Thus, the fading
coefficients can be predicted for beyond the coherence time.
When the future samples is known the modified received signal on the output of the matched filter is given by
where ![]() is prediction of fading channel.
is prediction of fading channel.
When ![]() we have perfect estimation and
fast fading channel becomes the AWGN channel with average probability of bit
error rate (BER) that corresponds of a lower bounds for BPSK modulation
we have perfect estimation and
fast fading channel becomes the AWGN channel with average probability of bit
error rate (BER) that corresponds of a lower bounds for BPSK modulation
where 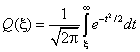 .
.
The upper bound obtained in [10] for Rayleight fading channel is
The eqs. (4) and (5) are the lower and
upper limits of the performance. Really, the value ![]() is
between this limits and below we will investigate
is
between this limits and below we will investigate ![]() depending of quality of channel
prediction.
depending of quality of channel
prediction.
3. DWT AND DWPT IN MATHEMATICS
The main
problem of the wavelets analysis is creating of basis functions for wavelets
systems. The synthesis of basis function is founded on the theory of
multiresolution analysis (MA) [4,8-11]. The sequence of closed subspaces ![]() of
of ![]() , is defined as a multiresolution
analysis of
, is defined as a multiresolution
analysis of ![]() if
are satisfied the following properties:
if
are satisfied the following properties:
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
4. If ![]() .
.
5.Such function ![]() (scaling function) with a non-vanishing
integral exists, that the collection of his shifts
(scaling function) with a non-vanishing
integral exists, that the collection of his shifts ![]() is a orthonormal basis of
is a orthonormal basis of ![]() .
.
Since ![]() a sequence hk
exists such that the scaling function satisfies the condition
a sequence hk
exists such that the scaling function satisfies the condition
The eq.(6) is refinement equation (or two scale difference equation). The Fourier transform of the scaling function is
where ![]() is a 2p-periodic function.
is a 2p-periodic function.
By integrating both sides of eq.(6), and dividing by the
non-vanishing integral of ![]() , we see that
, we see that ![]() , and as a consequence
, and as a consequence ![]() . The scaling function
meets the normalization condition
. The scaling function
meets the normalization condition ![]() and for its collection
and for its collection ![]() .
.
The collection of the functions
is the orthonormal basis of the space![]() .
.
In many applications, we never need the scaling function itself.
Instead we may often work directly with the hk. An orthogonal
scaling function is a function j(t) such that the set ![]()
![]() is an orthonormal basis of
is an orthonormal basis of ![]() and satisfies by the
next property
and satisfies by the
next property
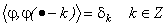 .
(9)
.
(9)
Using the Poisson summation formula [2], in the frequency domain we have
We consider the subspace ![]() as complementary space of
as complementary space of ![]() in
in ![]() ,
, ![]() , symbol Å is direct sum. If
the set
, symbol Å is direct sum. If
the set ![]() consists
on functions which spectrums are concentrated in interval
consists
on functions which spectrums are concentrated in interval ![]() , then
, then ![]() consists on the function with spectrum in
interval
consists on the function with spectrum in
interval ![]() and
and ![]() .
In other words, each element of
.
In other words, each element of ![]() can be written as the sum
can be written as the sum ![]() . The space
. The space ![]() contains
the detail information needed to go from an approximation at resolution j
to an approximation at resolution j+1. Consequently,
contains
the detail information needed to go from an approximation at resolution j
to an approximation at resolution j+1. Consequently, ![]() .
.
A function ![]() is a wavelet if the collection
of his shifts
is a wavelet if the collection
of his shifts ![]()
![]() is a
orthonormal basis of
is a
orthonormal basis of ![]() .
The function
.
The function
is an orthonormal basis of ![]() . Since
the subspaces
. Since
the subspaces ![]() are
mutually orthogonal, the collection of functions
are
mutually orthogonal, the collection of functions ![]() is an orthonormal basis of L2(R).
is an orthonormal basis of L2(R).
Each element in a given system has compact support in time and
frequency. Since the wavelet ![]() a sequence gk exists
such that
a sequence gk exists
such that
where ![]() and
and ![]() , ¾ is the sign of
conjugation.
, ¾ is the sign of
conjugation.
The Fourier transform of the wavelet is given by
where ![]() is a 2p-periodic function and
is a 2p-periodic function and ![]() .
.
The basis of ![]() have the orthonormal property. In this
case
have the orthonormal property. In this
case
The eq.(14) in
the frequency domain is ![]() .
.
The sufficient condition for a
multiresolution analysis to be orthogonal is ![]() or
or
The eq.(15) in the frequency domain has a form
The decomposition
of any given function in space![]() can be presented as
can be presented as
where 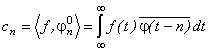 .
.
Taking into
account that ![]() and
applying of eq.(17) we write
and
applying of eq.(17) we write
According with Lemma [9] we have
Multiplying
eq.(18) at ![]() and
applying eq.(9), (15) and Lemma we get
and
applying eq.(9), (15) and Lemma we get
![]() ½ ´
½ ´ ![]()
Multiplying
eq.(18) at ![]() and
applying eq.(14) we get
and
applying eq.(14) we get
In general case ![]() and we have equation
and we have equation
From eq.(22) the
coefficients ![]() and
and
![]() can be define
as
can be define
as
Replacing ![]() y
y ![]() we get
we get
The eq. (24) is direct discrete
fast wavelet transform that consists from 2 convolutions, and ![]() is initial coordinates
of any function in the space
is initial coordinates
of any function in the space![]() , where
, where ![]() . Applying the similar manner by multiplying
(22) at
. Applying the similar manner by multiplying
(22) at ![]() we have
we have
Therefore we have inverse fast wavelet transform
One of the powers of wavelet technology is the ability to choose the defining coefficients for a given wavelet system to be best adapted to the given problem. Daubechies developed in her original paper [4] specific families of wavelet systems which had maximal vanishing moments of the function and which were very good for representing polynomial behavior.
4. PYRAMIDAL STRUCTURE OF THE WAVELET TRANSFORM
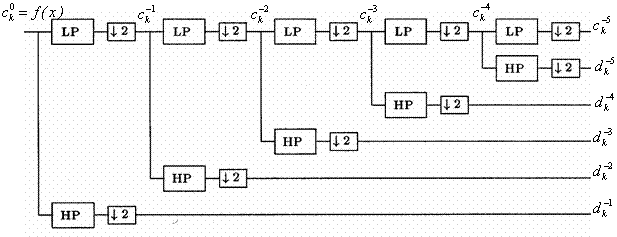
As follows from (24) and (26) the forward and inverse wavelet transform can be implemented using a set of upsamplers, downsamplers and recursive two-channel filter banks, that named also pyramidal algorithm because has pyramidal structure. At [1,2] has shown that the tree or pyramid algorithm can be applied to the wavelet transform by using the wavelet coefficients for calculate the filter coefficients of the QMF (Quadrature Mirror Filter) filter pairs.
The same wavelet coefficients are used in both the low-pass (LP) and
high-pass (HP) (actually, band-pass) filters. The low-pass filter coefficients ![]() are associated with the
scaling function. The output of each low-pass filter is
are associated with the
scaling function. The output of each low-pass filter is ![]() , or approximation components, of
the original signal for that level of the tree. The high-pass filter
coefficients
, or approximation components, of
the original signal for that level of the tree. The high-pass filter
coefficients ![]() is
associated with the wavelet function (note the alternating sign change)
is
associated with the wavelet function (note the alternating sign change) ![]() .
.
The output of each high-pass filter is the ![]() ,
,![]() or detail components, of the original
signal. The
or detail components, of the original
signal. The ![]() of
the previous level are used to generate the new
of
the previous level are used to generate the new ![]() and
and ![]() for the next level of the tree. Decimation
by two corresponds to the multiresolution nature (the j parameter) of
the scaling and wavelet functions (Figure 1).
for the next level of the tree. Decimation
by two corresponds to the multiresolution nature (the j parameter) of
the scaling and wavelet functions (Figure 1).
Figure 1. Direct pyramidal structure of DWT
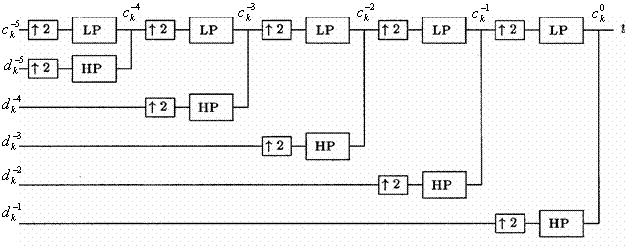
The reverse fast wavelet transform essentially performs the
operations associated with the forward fast wavelet transform in the opposite
direction (Figure 2). The expansion coefficients are combined to reconstruct
the original signal. The same ![]() ,
,![]() coefficients are used as in the forward
transform, but in reversed order. The process works down the branches of the
tree combining the approximation and detail signals into approximation signals
with higher levels of detail.
coefficients are used as in the forward
transform, but in reversed order. The process works down the branches of the
tree combining the approximation and detail signals into approximation signals
with higher levels of detail.
Figure 2. Inverse pyramidal structure of DWT
Instead of decimation, the signals are interpolated: zero’s are placed between each approximation and detail sample, and the signals are then passed through the low-pass and high-pass filters. The intermediate 0 values are replaced by "estimates" derived from the convolutions. The filters' outputs are then summed to form the approximation coefficients for the next higher level of resolution. The final set of approximation coefficients at the tree's top level in the reverse transform is a reconstruction of the original signal data points.
As follows from eq.(24) and (26) the signal
decomposition depends on the impulse responses of the LP and HP filters, that
in turn depends on the choosing of scaling and wavelets function. The function ![]() and
and ![]() can be interpreted as coefficients of the
series for the functions
can be interpreted as coefficients of the
series for the functions ![]() and
and ![]() and have the forms
and have the forms
In signal processing terminology, the various bases of the DWT can be used by choosing the corresponding coefficients of filter banks.
The packet of wavelets can be obtain when the spaces V and W of each stage are divided by own spaces V and W. In this case the wavelet packet transform is presented as a subspace decomposition tree. In the fundamental of the wavelets packet is the fact, called the splitting trick [8,9]:
Lets arbitrary function ![]() defined so that the set
of function
defined so that the set
of function ![]() is
a ortonormal basis and
is
a ortonormal basis and ![]() ,
, ![]() , then the sets of functions
, then the sets of functions ![]() and
and ![]() is ortonormal basis over the
set of function
is ortonormal basis over the
set of function ![]() as
well.
as
well.
It means that we obtained from one
orthogonal space two orthogonal spaces where ![]() ,
, ![]() .
.
In application of classical
multiresolution analysis the splitting trick for ![]() are
are ![]() and
and![]() . The wavelet packets are the basis
function for each subspases, not only for
. The wavelet packets are the basis
function for each subspases, not only for ![]() , but for
, but for ![]() as well. So, after L splitting we
have
as well. So, after L splitting we
have ![]() basis
function. In this case the wavelet packet transform is presented as a subspace
decomposition tree (Figure 3).
basis
function. In this case the wavelet packet transform is presented as a subspace
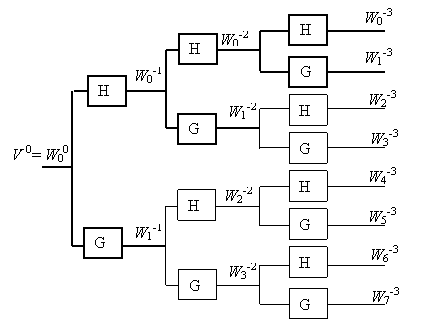
decomposition tree (Figure 3).
The bolt line in figure 3 is the
classical multiresolution analysis where ![]() ,
, ![]() .
. ![]() is the space of the basis with number j,k,
where j = -1,-2,.... is number of level of the tree and
is the space of the basis with number j,k,
where j = -1,-2,.... is number of level of the tree and ![]() is the number of branch
of the j-th level. As follows from Figure 3 each space of the function
is the number of branch
of the j-th level. As follows from Figure 3 each space of the function ![]() is generating the
subspaces
is generating the
subspaces ![]() and
and ![]() , so that
, so that ![]() , or for orthogonal basis
is truth that
, or for orthogonal basis
is truth that
Figure 3. Subspace decomposition tree for DWPT
As demonstrated in [8,9] the direct sum of the subspaces ![]() is complete orthogonal basis of the initial space. For the each spaces
is complete orthogonal basis of the initial space. For the each spaces ![]() , the
function
, the
function ![]() correspond,
so that this function is orthonormal basis of
correspond,
so that this function is orthonormal basis of ![]() . Its take a place the following recursive
sequence for pare of quadrature mirror filters H and G with
impulse response
. Its take a place the following recursive
sequence for pare of quadrature mirror filters H and G with
impulse response ![]() and
and
![]() :
:
where ![]() ,
, ![]() .
.
The functions ![]() and
and ![]() are the scaling and wavelet
functions respectively from classical MRA (in the Figure 3 it corresponds the
bold line) and then the “parent” function
are the scaling and wavelet
functions respectively from classical MRA (in the Figure 3 it corresponds the
bold line) and then the “parent” function ![]() generates the “children” functions
generates the “children” functions ![]() and
and ![]() .
.
The functions ![]() and
and
![]() have the
properties of orthogonal to itself and its pare, e.g.
have the
properties of orthogonal to itself and its pare, e.g.
Therefore the wavelet packet transform for any function ![]() will be presented in the
form
will be presented in the
form
where j =
-1,-2,…,-k is number of level of the direct tree,![]() is number of branches in the j-th
level.
is number of branches in the j-th
level.
The inverse wavelet packet transform
where j =
-k,-k+1,…,-1 is number of level of the inverse tree,![]() is number of branches
in the j-th level.
is number of branches
in the j-th level.
6. FADING CHANNEL ESTIMATION
We consider applying of DWT and DWPT for fading channel estimation. As the basic method will be used the maximum entropy method [6,7] in which instead of spectral Fourier coefficients have been used the coefficients of DWT or DPWT calculated according to eqs.(24), (26) and (33),(34).
We will use the classical method of prediction using AR-model for an estimation of a forward linear prediction of flat fading channel coefficients xn, n =1,2...,N + p and xn = 0 at n < 1, n > N
where ![]() is estimation of element of xn ,
ak is a coefficients of prediction filter, N is number of
estimated elements, p is order of AR - model.
is estimation of element of xn ,
ak is a coefficients of prediction filter, N is number of
estimated elements, p is order of AR - model.
If minimize an error of a linear
prediction ![]() ,
then a vector of a linear
,
then a vector of a linear
prediction parameters ak which
minimizes the average square of an error ![]() is the solution of the normal equations
is the solution of the normal equations
where ![]() is (p + 1)
vector,
is (p + 1)
vector, ![]() ,
,![]() ,
,
![]() , ~ is
symbol of transpose and conjugate, T is transpose symbol,
, ~ is
symbol of transpose and conjugate, T is transpose symbol, ![]() is Toeplitz (p+1)´(p+1)
correlation matrix of input data, X is (N+p)´ (p+1)
matrix of input data with structure as shown below
is Toeplitz (p+1)´(p+1)
correlation matrix of input data, X is (N+p)´ (p+1)
matrix of input data with structure as shown below
The eq.(36) is the Yule-Walker equation for autoregressive process and can be solved concerning to parameters ai, i = 1,2..., p by various known algorithms, for example by Levinson algorithm [7]. In particularly if the inverse matrix has a form
Then the solution of eq.(36) is
The solution (39) allows obtaining the spectral density of input data for the received parameters with maximum entropy
were ![]() is estimation of parameter an,
, Dt
is a sampling interval.
is estimation of parameter an,
, Dt
is a sampling interval.
For prediction of nonstationary sequences more referable introduce the exponential window that is gone along the input data, creating the least change of the current errors and very strongly reducing of older ones. Thus, the parameter r we put as
were w is positive real scalar satisfying to a condition 0 < w £ 1. Then expression for a matrix R we can write
where ![]() is n-th row of matrix X , n
= 1,2..., N+p.
is n-th row of matrix X , n
= 1,2..., N+p.
We will consider and then compare for criteria of minimum mean square prediction errors 4 basic algorithm of fading channel estimation:
Algorithm1. Classical method of prediction that uses AR-model without sliding window:
Step 1. Obtaining of current input data element xk, k=1,2,…,N+p.
Step 2. Forming matrix of input data X according of eq.(37).
Step 3. Calculation of a matrix ![]() and vector A
using eqs.(38) and (39).
and vector A
using eqs.(38) and (39).
Step 4. Estimation of a forward linear prediction of elements xn with eq. (35).
Algorithm2. Classical method of prediction with sliding window, that consists from the following steps:
Step 1. Obtaining of current input data element xk, k=1,2,…,N+p.
Step 2. Forming and waiting of n´(p + 1) input data matrix X
where ![]() , n = 1,2, …, N +p is
number of the current element.
, n = 1,2, …, N +p is
number of the current element.
Step 3. Calculation of a matrix ![]() and vector A
using eqs.(38) and (39).
and vector A
using eqs.(38) and (39).
Step 4. Estimation of a forward linear prediction of elements xn with eq.(35).
Algorithm 3. Prediction algorithm that uses DWT.
Step 1. Obtaining of current input data element xk, k =1,2,…,N+p.
Step 2. Calculating the DWT of the input data in the finite interval and defining the DWT
coefficients.
where ![]() is the initial sampled the fading signal.
is the initial sampled the fading signal.
Step 3. Carrying out of forward linear prediction of wavelets coefficients for each level of
scale.
where the coefficients ![]() of the prediction filter
determined similar as in eq.(39).
of the prediction filter
determined similar as in eq.(39).
Step 4. Obtaining the predicted data using inverse DWT with prediction coefficients.
where ![]() is the predicted fading signal.
is the predicted fading signal.
Algorithm 4. Prediction algorithm that uses DWPT.
Step 1. Obtaining of current input data element xk, k =1,2,…,N+p.
Step 2. Calculating the DWT of the input data in the finite interval and defining the DWPT
coefficients.
where ![]() is initial sampled fading signal.
is initial sampled fading signal.
Step 3. Carrying out of forward linear prediction of wavelets coefficients for each level of
scale.
where the coefficients ![]() of the prediction filter
determined similar as in eq.(39).
of the prediction filter
determined similar as in eq.(39).
Step 4. Obtaining the predicted data using inverse DWPT with prediction coefficients.
where ![]() is predicted fading signal.
is predicted fading signal.
The variety of orthonormal bases which can be formed by the Discrete Wavelet Transform algorithm, coupled with the infinite number of wavelet and scaling functions which can be created, yields a very flexible analysis tool. Not only can the best wavelet be chosen to analyze a particular signal but the best orthonormal basis as well. But in many applications as shows the practice the Daubechies wavelets are optimum at concentrating the signal power into the lower-scale transform coefficients. As a result, there is less "risk" in the prediction.
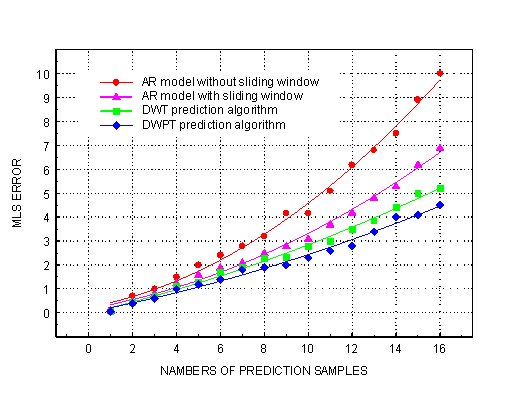
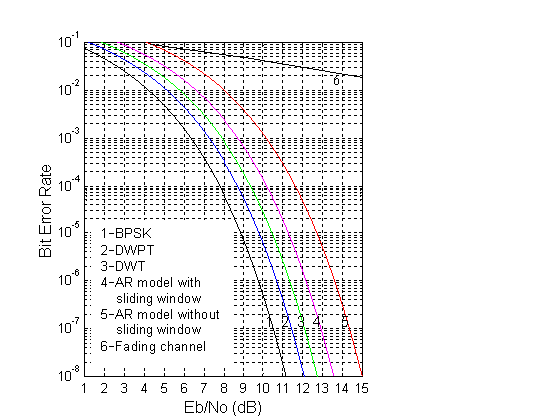
The flat fading channel was simulated by three scatters in the presence of AWGN without channel parameter variation. The Doppler frequencies correspond to 100, 50 and 30 Hz with signal/noise rations 8, 6, 9db. The sampling frequency of the channel is 240 Hz. The channel is observed for the first 150 samples. The LMS error between the actual and prediction envelopes for the 4 prediction algorithms was obtained. The result is presented in Figura.4. In the bit error rate (BER) simulation was applied coherent detection and BPSK modulation. The simulation result is presented in Figura.5, where the lower and upper bounds was obtained with eq.(4) and eq.(5).
As follows from Figure 4, the estimation of the fading channel with application DWT and DWPT allows to decrease the square average prediction error in comparison with methods that use AR-model 1.5 ¸2.5 times. As follows at the Figura.5, the performance can be increased by ~ 1¸3 dB with application of WPT and DWPT prediction methods. As the simulation results has shown obtaining relations have very weak depending on the number of scatters in fading channel.
Figure 4. Comparison of estimation channel algorithms by the minimum least square error criteria.
Figure 5. Performance of the radio communications for different estimation channel algorithms
8. CONCLUSION
In this paper the application of Discrete Wavelet Transform and Discrete Wavelet Packet Transform to fading channel estimation was presented. The comparative analysis of 4 estimated algorithms was carry out: two algorithms based on AR-model (with sliding window and without sliding window), algorithm that uses Discrete Wavelet Transform and algorithm that uses Discrete Wavelet Packet Transform. As it is shown, the application of DWT in maximum entropy prediction method is allows decrease the square average prediction error in comparison with methods that used AR model with sliding window and without sliding window at 1.5 ¸2.5 times when number of prediction samples is 16. It shown that performance of the radio communications with application DWT and DWPT can be increase the capacity of the channel up to ~ 1¸3 dB comparing with conventional methods based on AR-model. This goal obtained due to more detailed analysis of flat fading channel that received from coefficients of DWT and DWPT.
9. REFERENCES
1. Akansu A.N., Smith M.J.T., Subband and Wavelet Transforms: Design and Applications, Kluwer, 1996.
2. Benedetto J., Wavelets, Mathematics and Applications, Press New York, 1994, 574p.
3. Cody, Mac A. “Wavelet Transforms as Applied to Financial Market Analysis”, Issue of the conference “Evolving Complexity Challenges to Society, Economy and the Individual”, The University of Texas at Dallas, Nov., 1994
4. Daubechies I., Ten Lectures on Wavelets, SIAM,v.61,1992.
5. Eyceoz T., Duel-Hallen A.,andHallen H.,“Deterministic Channel Modeling and Long Range Prediction of Fast Fading Mobile Radio Channels ”,IEEE Comm.Letters ,Vol.2,No.9,pp.254 –256,Sept.1998.
6. Haykin S. Adaptive Filter Theory, New Jersey, Prentice Hall, 1996.
7. Marple S.L. Jr., Digital spectral analysis with application, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1987.
8. Meyer Y., Wavelets: Algorithms and Applications, Cambrige University Press, 1993.
9. Petukhov A.P. The introduction in theory of wavelets bases, St.Peterburg,1999.
10. Proakis J.G., Digital Communications, McGraw-Hill, New York,1995.
11. Strang G., Nguyen T., Wavelets and filter banks, Wellesley-Cambridge Press, 1996, 490p.
12. Zaharov V.V., Kokhanov A.B. “Discrete Wavelet Transform Application for Market Stock Rate Analysis” Issue of International Scientific Conference “Methods & Algorithms of Applied Mathematics in Engineering, Medicine And Economics”, Novocherkassk, Russia, Feb.2001, pp.30-34.
|
|
|
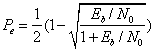 .
.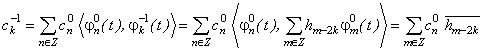 . (20)
. (20)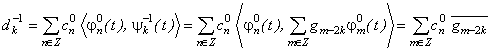 . (21)
. (21)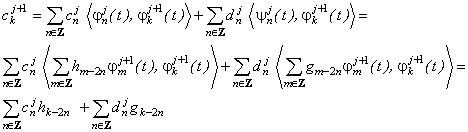 (25)
(25)
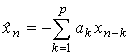 , (35)
, (35) .
.
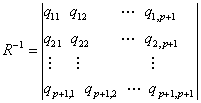 .
.
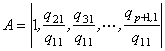 .
.
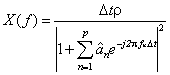 ,
(40)
,
(40)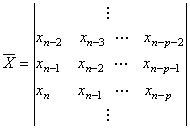 (44)
(44)