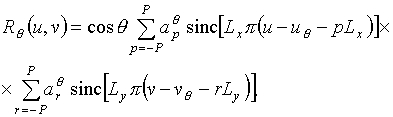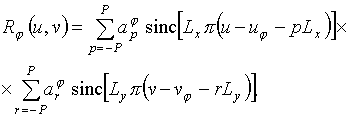|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2001 |  |
ЗАДАЧА СИНТЕЗА АНТЕННОЙ РЕШЕТКИ ПРОИЗВОЛЬНОЙ ГЕОМЕТРИИ ПО ЗАДАННОЙ ВЕКТОРНОЙ ДИАГРАММЕ НАПРАВЛЕННОСТИ
Д. Д. Габриэльян, С. Е. Мищенко
Ростовский военный институт ракетных войск
Получена 5 сентября 2001 г.
В работе предлагается общий метод нахождения векторов электрических и магнитных токов в излучателях антенной решетки с эллиптической поляризацией сигнала в виде суперпозиции решений задач синтеза антенных решеток с линейной поляризацией сигнала. Получены соотношения, позволяющие в зависимости от типа излучателей и конфигурации решетки свести задачу синтеза по заданной векторной диаграмме направленности к двум независимым задачам синтеза антенных решеток с линейной поляризацией сигнала. Приведены результаты численных исследований.
В радиотехнических системах различного назначения часто используются антенные решетки (АР) с эллиптической поляризацией сигнала. Для антенн данного типа определение комплексных амплитуд возбуждения излучателей по заданной векторной диаграмме направленности (ДН) представляет интерес не только в практическом, но и теоретическом плане. Это обусловлено тем, что использование общих подходов, изложенных в работах [1-2], требует решения ряда вопросов. В частности, в данных работах рассматриваются задачи синтеза антенн с линейной поляризацией сигнала. Кроме того, распространение известных подходов на случай трехмерного раскрыва и излучателей, в которых существует одновременно несколько компонент электрического и (или) магнитного токов, встречает определенные трудности.
В отдельных работах, например [3-4], рассмотрены частные вопросы синтеза АР по заданной векторной ДН, однако общие подходы к решению данных задач отсутствуют.
Цель данной статьи заключается в определении общего метода нахождения векторов электрических и магнитных токов в излучателях АР с эллиптической поляризацией сигнала в виде суперпозиции решений задач синтеза АР с линейной поляризацией сигнала.
Рассмотрим антенную решетку M излучателей. Пусть в соответствии с [1] известны:
а) координаты излучателей
и функции
![]() ,
,
![]() (
(![]() ; m=1,2,…,M);
; m=1,2,…,M);
![]() ;
;
![]() ;
;
![]() - углы, определяющие направление в
пространстве; индексы e, -
указывают, что источником поля является электрический или магнитный ток
соответственно;
- углы, определяющие направление в
пространстве; индексы e, -
указывают, что источником поля является электрический или магнитный ток
соответственно;
б) векторная функция
![]() - заданная векторная
ДН, где
- заданная векторная
ДН, где
![]() ,
,
![]() - орты сферической
системы координат;
- орты сферической
системы координат;
в) допустимая ошибка
![]()
отклонения синтезируемой
нормированной диаграммы
![]() от заданной. Здесь
от заданной. Здесь
![]() - вектор, элементами которого являются
отклонения соответствующих проекций заданной и синтезируемой векторных ДН.
Геометрия задачи приведена на рис. 1.
- вектор, элементами которого являются
отклонения соответствующих проекций заданной и синтезируемой векторных ДН.
Геометрия задачи приведена на рис. 1.
Требуется найти
обладающее минимальной нормой распределение комплексных амплитуд, которые
формируют векторную ДН
![]() , удовлетворяющую условию (1).
, удовлетворяющую условию (1).
Диаграмма направленности
![]() системы излучателей
определяется двумя компонентами в виде [1]
системы излучателей
определяется двумя компонентами в виде [1]
(2)
![]() ,
,
где
В соотношениях (3) и (4) W0 - волновое сопротивление свободного пространства;
![]() ,
,
![]() - комплексные амплитуды x-й составляющей электрического и
магнитного токов соответственно (
- комплексные амплитуды x-й составляющей электрического и
магнитного токов соответственно (![]() ) в m-м излучателе. Функции
) в m-м излучателе. Функции
![]() и
и
![]() (
(![]() ; m=1,2,…,M) определяют проекцию на
соответствующую ось векторной ДН антенной решетки при возбуждении m-го
излучателя
; m=1,2,…,M) определяют проекцию на
соответствующую ось векторной ДН антенной решетки при возбуждении m-го
излучателя
![]() -составляющей
стороннего электрического (индекс e) или стороннего магнитного (индекс
-составляющей
стороннего электрического (индекс e) или стороннего магнитного (индекс
![]() ) тока единичной амплитуды, в то время как
остальные излучатели нагружены на согласованные нагрузки.
) тока единичной амплитуды, в то время как
остальные излучатели нагружены на согласованные нагрузки.
Примерами излучающих элементов, в которых могут одновременно существовать независимо три составляющих тока являются излучатели, описанные в [5,6].
Из соотношений (2)-(4)
следует, что при необходимости реализации различных требований к
![]() - и
- и
![]() -компоненте векторной ДН должно
осуществляться независимое управление двумя составляющими электрического и
(или) магнитного тока в каждом излучателе.
-компоненте векторной ДН должно
осуществляться независимое управление двумя составляющими электрического и
(или) магнитного тока в каждом излучателе.
С помощью несложных
преобразований формулы (3) и (4) могут быть приведены к виду, связывающему
составляющие
![]() и
и
![]() (
(![]() ) с компонентами векторной
ДН. Такими соотношениями, например, могут являться
) с компонентами векторной
ДН. Такими соотношениями, например, могут являться
при управлении составляющими
![]() и
и
![]() в излучателях;
в излучателях;
при управлении составляющими
![]() и
и
![]() в излучателях;
в излучателях;
при управлении составляющими
![]() и
и
![]() в излучателях;
в излучателях;
при управлении составляющими
![]() и
и
![]() в излучателях;
в излучателях;
при управлении составляющими
![]() и
и
![]() в излучателях и
в излучателях и
при управлении составляющими
![]() и
и
![]() в излучающих элементах.
в излучающих элементах.
Так, в работах [3,4] были решены задачи синтеза АР по заданной векторной ДН для случаев (7) и (12) соответственно.
При этом компоненты
вектора
![]() в
первом случае описывались выражениями
в
первом случае описывались выражениями
Легко видеть, что
минимизация компонент вектора
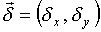 приведет к минимизации его нормы
приведет к минимизации его нормы
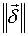 . В связи с этим задача
синтеза АР по заданной векторной ДН может быть сформулирована в виде двух
независимых задач оптимизации, в качестве целевых функций которых выступают
. В связи с этим задача
синтеза АР по заданной векторной ДН может быть сформулирована в виде двух
независимых задач оптимизации, в качестве целевых функций которых выступают
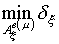 .
.
Решением задачи синтеза
являются коэффициенты
![]() (
(![]() ; m=1,2,…,M), обеспечивающие выполнение условия
(1).
; m=1,2,…,M), обеспечивающие выполнение условия
(1).
Заметим, что в случае
синтеза АР с линейной поляризацией (![]() или
или
![]() ) соотношения (7)-(12) сводятся к известным
задачам, рассмотренным, например, в [1,2].
) соотношения (7)-(12) сводятся к известным
задачам, рассмотренным, например, в [1,2].
Задача синтеза АР при
управлении составляющими
![]() и
и
![]() рассмотрена в [3], а
рассмотрена в [3], а
![]() и
и
![]() - в работе [4]. В данных работах отражена
принципиальная возможность формирования векторной ДН с использованием методов
синтеза АР. Для того, чтобы продемонстрировать возможности синтеза АР с
круговой поляризацией сигнала, рассмотрим пример, в котором формируется двухлучевая
ДН. Направление максимума первого луча - (
- в работе [4]. В данных работах отражена
принципиальная возможность формирования векторной ДН с использованием методов
синтеза АР. Для того, чтобы продемонстрировать возможности синтеза АР с
круговой поляризацией сигнала, рассмотрим пример, в котором формируется двухлучевая
ДН. Направление максимума первого луча - (![]() ), второго - (
), второго - (![]() ). В направлении (
). В направлении (![]() ) формируется только q-компонента поля, в направлении (
) формируется только q-компонента поля, в направлении (![]() ) - только
) - только
![]() -компонента.
-компонента.
Рассмотрим задачу синтеза
плоской 8x8 элементной АР точечных излучателей,
размещенных в узлах прямоугольной сетки с шагом 0,5![]() (рис. 1). Пусть конструкция
излучателей позволяет реализовать управление составляющими
(рис. 1). Пусть конструкция
излучателей позволяет реализовать управление составляющими
![]() и
и
![]() . С использованием выражений (7) определим
функции
. С использованием выражений (7) определим
функции
![]() ,
,
![]() в виде
в виде
где
![]() ;
;
![]() ; - координаты фазовых центров излучателей.
; - координаты фазовых центров излучателей.
Заметим, что при
возбуждении сигналом единичной амплитуды одного единственного n-го входа такой АР (например,
![]()
![]()
![]() , m=1,2,…,M,
, m=1,2,…,M,
![]() )
приведет к формированию изотропной ДН с линейной поляризацией сигнала. Таким
образом, использование выбранной модели при управлении только комплексными
амплитудами
)
приведет к формированию изотропной ДН с линейной поляризацией сигнала. Таким
образом, использование выбранной модели при управлении только комплексными
амплитудами
![]() или
или
![]() приводит к
модели плоской АР точечных изотропных излучателей.
приводит к
модели плоской АР точечных изотропных излучателей.
Определим функцию
![]() аналогично [3] с
использованием выражений
аналогично [3] с
использованием выражений
где sinc(*)- функции Котельникова;
![]() ,
,
![]() - постоянные коэффициенты (p=-P,-P+1,…,P); Lx, Ly - размер раскрыва рассматриваемой АР
вдоль одного из координатных направлений.
- постоянные коэффициенты (p=-P,-P+1,…,P); Lx, Ly - размер раскрыва рассматриваемой АР
вдоль одного из координатных направлений.
Пусть в рассматриваемом
случае P=1,
![]() ,
,
![]() ;
;
![]() (8-1), кроме того, положим
(8-1), кроме того, положим
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Решим задачу синтеза,
исходя из требования минимума величины
![]()
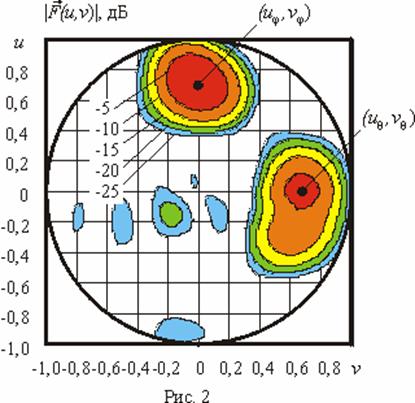
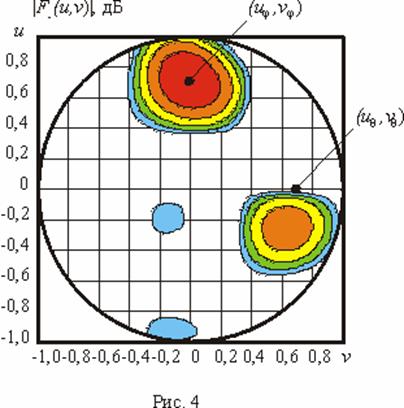
На рис. 2 приведено
контурное изображение двухлучевой объемной ДН
![]() рассматриваемой АР по полю, сформированной
в результате решения задачи синтеза.
рассматриваемой АР по полю, сформированной
в результате решения задачи синтеза.
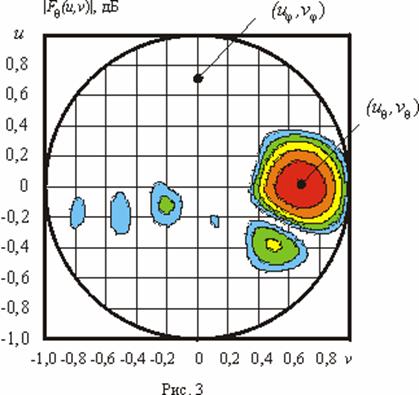
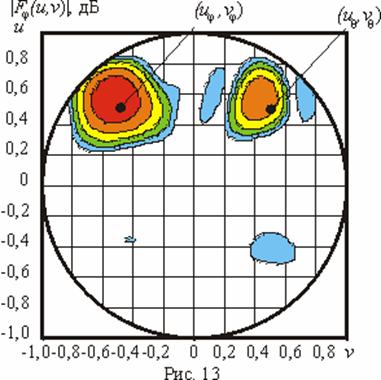
На рис. 3 и
рис. 4 приведены объемные
контурные ДН
![]() и
и
![]() ,
соответствующие
,
соответствующие
![]() -
и
-
и ![]() -компонентам
синтезированной ДН
-компонентам
синтезированной ДН
![]() соответственно.
Значения линий уровня на этих рисунках совпадают со значениями на
рис. 1. Приведенные
на данных рисунках ДН являются уже однолучевыми. Направления максимумов каждой
из компонент
соответственно.
Значения линий уровня на этих рисунках совпадают со значениями на
рис. 1. Приведенные
на данных рисунках ДН являются уже однолучевыми. Направления максимумов каждой
из компонент
![]() и
и
![]() в рассматриваемом случае
соответствуют направлениям с низким уровнем излучения ортогональных компонент.
в рассматриваемом случае
соответствуют направлениям с низким уровнем излучения ортогональных компонент.
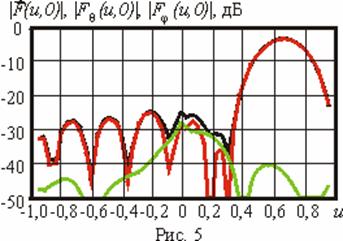
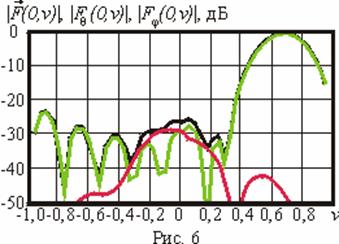
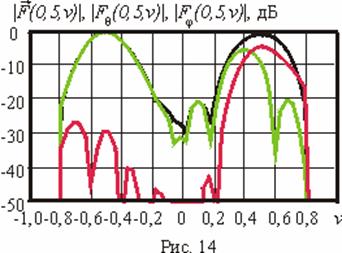
На рис. 5 и
рис. 6
представлены сечения формируемой ДН, проходящие через одно из направлений
максимума и начало обобщенной системы координат. Кривая, обозначенная черным
цветом, на данных рисунках соответствует сечениям синтезированной суммарной ДН
![]() , красная и зеленая
кривые - сечениям компонент
, красная и зеленая
кривые - сечениям компонент
![]() и
и
![]() соответственно.
соответственно.
Полученные результаты свидетельствуют не только о работоспособности предлагаемого метода, но и хорошо иллюстрируют практические возможности пространственно-поляризационной селекции. Помимо рассмотренного примера были проведены исследования и решена задача синтеза АР с круговой поляризацией для ряда других случаев.
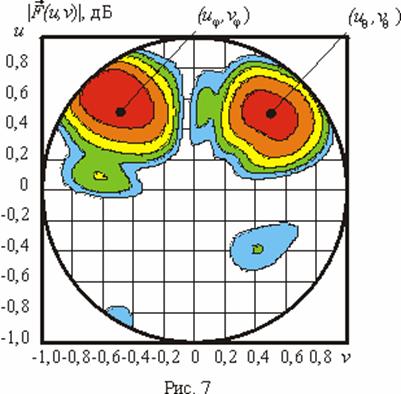
Сначала была решена
задача синтеза рассмотренной выше АР при
![]() ,
,
![]() ;
;
![]() ,
,
![]() . На рис. 7 приведено контурное изображение
двухлучевой объемной ДН
. На рис. 7 приведено контурное изображение
двухлучевой объемной ДН
![]() рассматриваемой АР по полю, сформированной
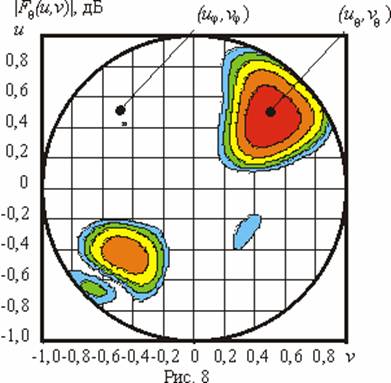
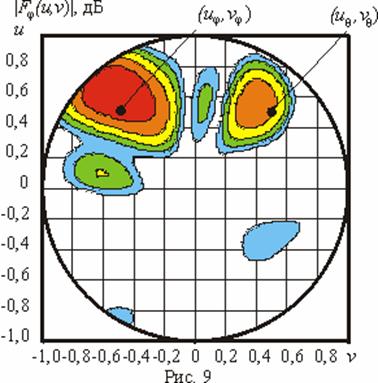
в результате решения задачи синтеза, а на рис. 8 и
рис. 9 - контурные ДН
рассматриваемой АР по полю, сформированной
в результате решения задачи синтеза, а на рис. 8 и
рис. 9 - контурные ДН
![]() и
и
![]() , соответствующие
, соответствующие
![]() - и
- и![]() -компонентам синтезированной ДН
-компонентам синтезированной ДН
![]() . Обозначения на данных
рисунках аналогичны введенным на рис. 2-4.
. Обозначения на данных
рисунках аналогичны введенным на рис. 2-4.
В данном случае оба луча
формируемой ДН
![]() могут
быть представлены на одном сечении. На рис. 10 приведены сечения ДН
могут
быть представлены на одном сечении. На рис. 10 приведены сечения ДН
![]() и ее компонент.
Обозначения на данном рисунке аналогичны обозначениям, введенным на
рис. 5.
и ее компонент.
Обозначения на данном рисунке аналогичны обозначениям, введенным на
рис. 5.
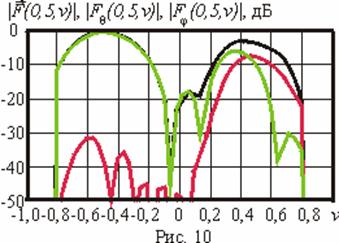
Полученные результаты показали, что, хотя полного подавления ортогональной компоненты в заданных направлениях не происходит, амплитуды сигналов отличаются по меньшей мере в два-три раза.
Похожая
задача была решена для плоской АР с излучателями, которые позволяли реализовать
управление составляющими
![]() и
и
![]() (выражения (11)). Заметим, что
применительно к такой конфигурации излучателей нельзя сформулировать первую из
решенных задач синтеза, что вытекает из анализа тригонометрических
сомножителей, входящих в выражения (11). В сечении
(выражения (11)). Заметим, что
применительно к такой конфигурации излучателей нельзя сформулировать первую из
решенных задач синтеза, что вытекает из анализа тригонометрических
сомножителей, входящих в выражения (11). В сечении
![]() невозможно реализовать
управление
невозможно реализовать
управление
![]() -компонентой
ДН АР, а в сечении u=0
- компонентой
-компонентой
ДН АР, а в сечении u=0
- компонентой
![]() .
Поэтому решенная задача соответствовала ориентации лучей
.
Поэтому решенная задача соответствовала ориентации лучей
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
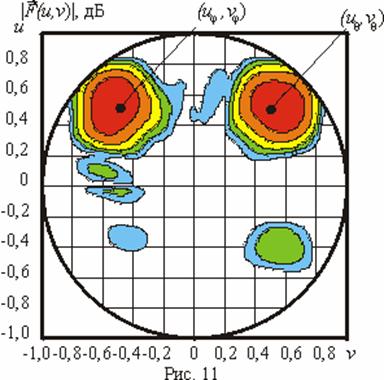
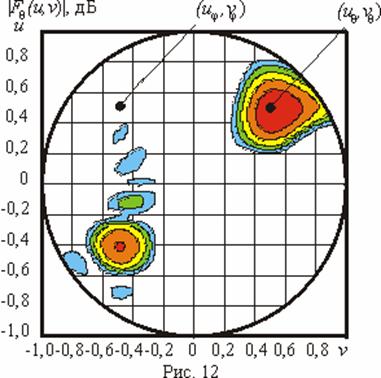
Совокупность результатов, полученных для данной задачи, приведена на рис. 11-14. Обозначения на данных рисунках аналогичны введенным ранее. Представленные результаты также показали работоспособность предложенного метода.
Таким образом, предлагаемый метод является развитием известных подходов к решению задач синтеза, так как позволяет решать задачи синтеза не только по заданной векторной, но и скалярной ДН. Кроме того, данный метод позволяет решать принципиально новые задачи, позволяющие обеспечивать не только пространственную, но и поляризационную селекцию полезного сигнала с помощью АР. Предложенный метод позволяет решать не только задачи амплитудно-фазового синтеза, что продемонстрировано в данной работе и работе [3], а также другие задачи, например, задачи фазового синтеза, решаемые в [4].
Полученные выражения (7)-(12), а также аналогичные выражения, которые могут быть построены на основании (2)-(4) позволяют не только формулировать требования к реализуемой заданной векторной ДН, но также позволяют и выбирать конфигурацию и тип излучателей, способных обеспечить выполнение требований, предъявляемые к ДН синтезируемой АР. Работа выполнена при финансовой поддержке РФФИ (код проекта № 01-01-00030).
СПИСОК ЛИТЕРАТУРЫ
1. Бахрах Л.Д., Кременецкий С.Д. Синтез излучающих систем (теория и методы расчета). М.: Радио и связь, 1974.
2. Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: фазированные антенные решетки и антенны с непрерывным раскрывом. М.: Сов. радио, 1980.
3. Габриэльян Д.Д., Мануилов Б.Д., Мищенко С.Е., Сариев К.Э. // РЭ. 2000. Т.45. № 3. С. 285.
4. Мищенко С.Е., Тупичкин Д.В. Фазовый синтез векторной диаграммы направленности плоской антенной решетки по методу проектируемого градиента // Сборник научных докладов IV международного симпозиума "ЭМС-2001". Санкт-Петербург, 19-22 июня 2001 г. С.417.
Авторы:
Габриэльян Дмитрий Давидович, Мищенко Сергей Евгеньевич,
e-mail:
jaguar@jeo.ru,
Ростовский военный институт ракетных войск
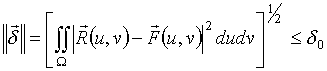
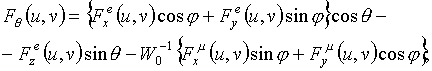
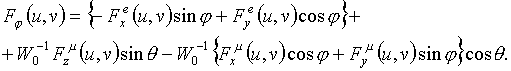
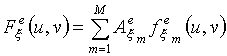 ,
,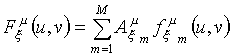 ;
;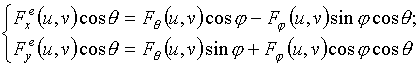
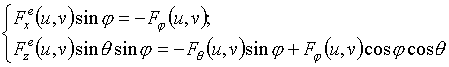
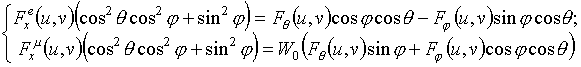
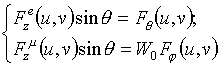
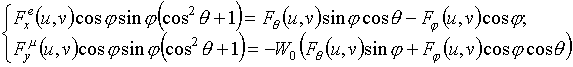
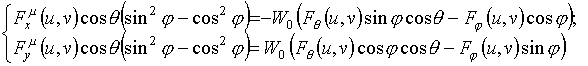
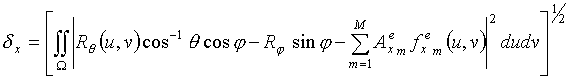 ;
;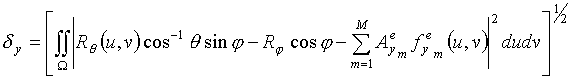 .
.