| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8 , 2000 |
О ВЛИЯНИИE ДВИЖЕНИЯ ДОМЕННОЙ ГРАНИЦЫ НА СПЕКТРАЛЬНЫЕ CВОЙСТВА УДЕРЖИВАЕМЫХ МАГНИТОСТАТИЧЕСКИХ ВОЛН
1 Ульяновское
отделение Института радиотехники и
электроники РАН, г. Ульяновск
![]() Институт радиотехники и электроники РАН , г.
Москва
Институт радиотехники и электроники РАН , г.
Москва
Получена 7 августа 2000 г.
В безобменном магнитостатическом приближении рассмотрены спектральные свойства поверхностных магнитостатических волн (ПМСВ) на равномерно движущейся доменной границе (ДГ) феррогранатового кристалла. Показано , что ПМСВ существенно модифицирует свою структуру и вид спектра под влиянием движения удерживающей границы. Установлено , что при уменьшении угла между волновым вектором ПМСВ и осью намагниченности, ПМСВ более подвержена параметрическому преобразованию за счет движения ДГ.
Отличительная особенность поверхностных магнитостатических волн (ПМСВ) в слоистых структурах магнитных материалов, широко применяемых для обработки сигнальной информации, состоит в их локализации границами раздела сред
[1]. Они также способны эффективно удерживаться доменными границами (ДГ) магнитных кристаллов, демонстрируя при этом существенную зависимость своих спектральных параметров от выбора направления распространения по отношению к внутренним полям в доменахПоведение магнитостатических и спиновых волн на движущихся ДГ рассматривалось в магнитодинамике в связи с проблемой их устойчивости при внешних воздействиях или поступательном перемещении
[4,6]. Внимание, поэтому, фиксировалось на установлении устойчивого режима движения ДГ и описании характера возмущений, развивающихся по внутренним (структурным) степеням свободы доменных стенок, что , например, имеет значение для решения проблемы генерации спиновых волн (см. [7,8]). Применительно к потребностям обработки сигнальной информации привлекательна, как раз, обратная ситуация, когда ДГ возмущается чрезвычайно (или достаточно) слабо и ей отводится единственная роль - каналировать магнитостатические (спиновые) волны, генерируемые внешним источником. С таких позиций влияние движения ДГ на спектральные свойства удерживаемых магнитостатических волн еще не оценевалось.В настоящей работе
рассмотрено распространение ПМСВ вдоль
равномерно движущейся в ферромагнетике (с
одноосной или кубической анизотропией) со
скоростью ![]() 180-градусной ДГ типа блоховской стенки.
Полагается, что в лабораторной (кристаллографической)
системе отсчета
180-градусной ДГ типа блоховской стенки.
Полагается, что в лабораторной (кристаллографической)
системе отсчета ![]() ДГ имеет (010)-ориентацию и перемещается
перпендикулярно оси
ДГ имеет (010)-ориентацию и перемещается
перпендикулярно оси ![]() спонтанного намагничения
спонтанного намагничения ![]() в доменах (
в доменах (![]() -
номер домена). Обозначим текущую координату
как
-
номер домена). Обозначим текущую координату
как ![]() ,
где
,
где ![]() -
время. Соответственно этому, принимая
границу раздела доменов геометрически
тонкой и бесструктурной (
-
время. Соответственно этому, принимая
границу раздела доменов геометрически
тонкой и бесструктурной (![]() -
волновое число ПМСВ ,
-
волновое число ПМСВ , ![]() -
толщина ДГ), спонтанным намагниченностям
-
толщина ДГ), спонтанным намагниченностям ![]() и внутренним магнитным полям
и внутренним магнитным полям ![]() в доменах (обуславливаются проявлением
магнитной анизотропии и действием внешних,
вообще говоря , неоднородных градиентных
магнитных полей, управляющих смещением ДГ)
предпишем значения:
в доменах (обуславливаются проявлением
магнитной анизотропии и действием внешних,
вообще говоря , неоднородных градиентных
магнитных полей, управляющих смещением ДГ)
предпишем значения:
где ![]() при
при ![]() при
при ![]() .
.
Во избежании
учета процессов структурной динамической
перестройки и самовозбуждения блоховской
стенки при ее перемещении [9] ,
условимся, что кристалл находится вдали от
фазового перехода , а ![]() достаточно мало по сравнению с предельной
уокеровской скоростью движения ДГ. При
нарушении оговоренных условий необходимо
рассматривать типичную для
магнитодинамики задачу описания движения
ДГ с учетом различных аспектов ее
динамической устойчивости в духе работ [4-6,9].
достаточно мало по сравнению с предельной
уокеровской скоростью движения ДГ. При
нарушении оговоренных условий необходимо
рассматривать типичную для
магнитодинамики задачу описания движения
ДГ с учетом различных аспектов ее
динамической устойчивости в духе работ [4-6,9].
Примем далее
, что ПМСВ распространяется под углом ![]() к оси
к оси ![]() и имеет
волновой вектор
и имеет
волновой вектор ![]() .
Ограничиваясь магнитостатическим
безобменным приближением будем полагать,
что длина волны ПМСВ много меньше
характерного размера кристалла. В таких
условиях граничные эффекты на внешних
границах ферромагнетика и его форма не
влияют существенно на поведение ПМСВ и
могут не учитываться.
.
Ограничиваясь магнитостатическим
безобменным приближением будем полагать,
что длина волны ПМСВ много меньше
характерного размера кристалла. В таких
условиях граничные эффекты на внешних
границах ферромагнетика и его форма не
влияют существенно на поведение ПМСВ и
могут не учитываться.
Для
построения решения перейдем из
лабораторной системы отсчета в систему
покоя ДГ ![]() .
Поскольку
.
Поскольку ![]() (
(![]() - скорость света
), то связь координат выразится
преобразованием Галилея:
- скорость света
), то связь координат выразится
преобразованием Галилея:
Используемые
для определения магнитных потенциалов ![]() уравнение Уокера и стандартные граничные
условия магнитостатики [10] не
содержат временных производных . Поэтому
они не изменят своего вида с переходом в
систему покоя ДГ. Однако содержащиеся в них
компоненты тензора магнитной
проницаемости
уравнение Уокера и стандартные граничные
условия магнитостатики [10] не
содержат временных производных . Поэтому
они не изменят своего вида с переходом в
систему покоя ДГ. Однако содержащиеся в них
компоненты тензора магнитной
проницаемости ![]() и
и ![]() зависят от частоты
зависят от частоты ![]() ,
которая с учетом (2) преобразуется согласно
замене:
,
которая с учетом (2) преобразуется согласно
замене: ![]() .
Здесь
.
Здесь ![]() -
частота колебаний в системе покоя ДГ ,
-
частота колебаний в системе покоя ДГ , ![]() -
характеристический коэффициент,
устанавливающий зависимость решения от
координаты
-
характеристический коэффициент,
устанавливающий зависимость решения от
координаты ![]() .
Таким образом, в качестве исходного
уравнения имеем уравнение Уокера
.
Таким образом, в качестве исходного
уравнения имеем уравнение Уокера
при следующих граничных условиях
![]()
Величины ![]() и
и ![]() имеют
при этом вид
имеют
при этом вид
где ![]() - магнитомеханическое отношение.
- магнитомеханическое отношение.
Как видно из
уравнений (3) и (5),
структура ПМСВ и доплеровский сдвиг
частоты будет определятся величиной ![]() .
В общем случае (произвольный угол
.
В общем случае (произвольный угол ![]() )
из (3),(5) следует , что
)
из (3),(5) следует , что
где знаки
коэффициента граничной локализации ![]() ПМСВ выбраны по условию ограниченности
решения в доменах. Решение (3) ищем
в виде
ПМСВ выбраны по условию ограниченности
решения в доменах. Решение (3) ищем
в виде
Здесь ![]() .
После подстановки (7) в (3),(4)
из условия разрешимости образующейся
системы однородных алгебраических
уравнений относительно амплитуд
.
После подстановки (7) в (3),(4)
из условия разрешимости образующейся
системы однородных алгебраических
уравнений относительно амплитуд ![]() получим дисперсионное соотношение для ПМСВ
на движущейся ДГ:
получим дисперсионное соотношение для ПМСВ
на движущейся ДГ:
![]() ,
(8)
,
(8)
где ![]()
![]() .
.
В случае
поперечного распространения к оси
намагниченности ![]() из (8) можно получить
из (8) можно получить
Согласно (9)
при ![]() ПМСВ в структурном отношение аналогична
обычной коллинеарной (
ПМСВ в структурном отношение аналогична
обычной коллинеарной (![]() )
поверхностной волне без доплеровского
сдвига частоты. При углах отличных от
)
поверхностной волне без доплеровского
сдвига частоты. При углах отличных от ![]() частота волны
частота волны ![]() претерпевает вследствие движения ДГ
доплеровский сдвиг, а фронт ее, из-за
присутствия радиационного добавка
претерпевает вследствие движения ДГ
доплеровский сдвиг, а фронт ее, из-за
присутствия радиационного добавка ![]() ,
разворачивается в сторону движения ДГ:
,
разворачивается в сторону движения ДГ: ![]() .
Из рис.1,2 видно, что с
уменьшением угла
.
Из рис.1,2 видно, что с
уменьшением угла ![]() наклон фронта увеличивается (растет модуль
вектора
наклон фронта увеличивается (растет модуль
вектора ![]() )
и увеличивается делокализация ПМСВ (уменьшается
коэффициент
)
и увеличивается делокализация ПМСВ (уменьшается
коэффициент ![]() ).
Расчеты для этих и последующих рисунков
выполнены для железоиттриевого граната с
параметрами
).
Расчеты для этих и последующих рисунков
выполнены для железоиттриевого граната с
параметрами ![]() ,
,
![]() . Для
нормировки скорости ДГ использовалось
значение скорости
. Для
нормировки скорости ДГ использовалось
значение скорости
акустических
поперечных волн ![]()
![]() .
.
При
продольном распространении ПМСВ ![]() дисперсионные соотношения согласно (8)
в случае
дисперсионные соотношения согласно (8)
в случае ![]() имеют вид:
имеют вид:
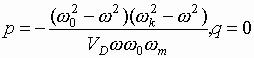 ,
(10)
,
(10)
где ![]() .
Выражения (10) свидетельствуют об
объемном характере распространения
магнитостатичекой волны, которая в случае
статичной ДГ (
.
Выражения (10) свидетельствуют об
объемном характере распространения
магнитостатичекой волны, которая в случае
статичной ДГ (![]() )
вырождается в однородные
магнитостатические колебания:
)
вырождается в однородные
магнитостатические колебания: ![]() .
К аналогичному выводу приводят результаты
Гилинского И.А. [2] для системы
эквидистантных ДГ.
.
К аналогичному выводу приводят результаты
Гилинского И.А. [2] для системы
эквидистантных ДГ.
Рис. 1 Зависимость
модуля вектора ![]() от скорости ДГ
от скорости ДГ ![]() :
:
1-![]() , 2-
, 2-![]() ,
3-
,
3-![]() , 4-
, 4-![]() ,
5-
,
5-![]() ;
; ![]() .
.
Рис. 2 Зависимость
коэффициента амплитудного спадания ![]() от скорости ДГ
от скорости ДГ ![]() :
:
1-![]() , 2-
, 2-![]() ,
3-
,
3-![]() , 4-
, 4-![]() ,
5-
,
5-![]() ;
; ![]() ;
;
![]() - коэффициент
амплитудного спадания на статичной ДГ.
- коэффициент
амплитудного спадания на статичной ДГ.
Спектр ПМСВ на
движущейся ДГ без учета потерь для ряда
углов ![]() показан в плоскости спектральных
переменных
показан в плоскости спектральных
переменных ![]() на рис.3 штриховыми кривыми.
на рис.3 штриховыми кривыми.
Рис.3 Спектральная
зависимость ![]() от
от ![]() .Тонкие
сплошные прямые -
.Тонкие
сплошные прямые - ![]() :
1-
:
1-![]() , 2-
, 2-![]() ,
3-
,
3-![]() , 4-
, 4-![]() .
Штриховые (сплошные жирные с учетом
затухания при
.
Штриховые (сплошные жирные с учетом
затухания при ![]() )
кривые без учета затухания (
)
кривые без учета затухания (![]() )
при
)
при![]() :
6-
:
6-![]() , 7-
, 7-![]() ,
8-
,
8-![]() , 9-
, 9-![]() .
.
Здесь же
тонкие прямые линии представляют частотные
дуплеты ![]() для
статичной ДГ. Наличие их вытекает в
высокочастотном пределе (переход к
уединенной ДГ) из спектра
магнитостатических волн в периодических
доменных структурах [2,3].
При этом в [2] , хотя и без ясного
обоснования, оговаривалось необходимость
отбрасывания в решении спектральной линии
дуплета
для
статичной ДГ. Наличие их вытекает в
высокочастотном пределе (переход к
уединенной ДГ) из спектра
магнитостатических волн в периодических
доменных структурах [2,3].
При этом в [2] , хотя и без ясного
обоснования, оговаривалось необходимость
отбрасывания в решении спектральной линии
дуплета ![]() (тонкая прямая линия 5 на рис.3).
(тонкая прямая линия 5 на рис.3).
Движение
устраняет моночастотность спектральных
линий и придает распространению ПМСВ
сигнальный характер. При ![]() происходит моночастотное замыкание
образующихся дисперсионных ветвей за
корневой точкой
происходит моночастотное замыкание
образующихся дисперсионных ветвей за
корневой точкой ![]() с координатами
с координатами ![]() в штриховую линию на частоте
в штриховую линию на частоте ![]() .
Для других углов
.
Для других углов![]() моночастотный предел за корневыми точками
моночастотный предел за корневыми точками ![]() сменяется спадающей зависимостью
сменяется спадающей зависимостью ![]() от
от
![]() .
.
Рис.4 Зависимость
![]() от
от ![]() .
Штриховые (сплошные жирные с учетом
затухания при
.
Штриховые (сплошные жирные с учетом
затухания при ![]() )
кривые без учета затухания (
)
кривые без учета затухания (![]() )
при
)
при ![]() :
:
1-![]() , 2-
, 2-![]() ,
3-
,
3-![]() , 4-
, 4-![]() .
.
На рис.4
приведены соответствующие спектрам рис.
3 зависимости ![]()
![]() от
от ![]() с
точками
с
точками ![]() ветвления , которые соответствуют точкам
ветвления , которые соответствуют точкам ![]() . Видно, что в бездиссипативном случае за
точками ветвления частота
. Видно, что в бездиссипативном случае за
точками ветвления частота ![]() становится комплексной . Это приводит к
неустойчивости связанных ПМСВ, описываемых
высокочастотными и низкочастотными
участками штриховых кривых. Такого рода
неустойчивость связанных ПМСВ хорошо
известна в электродинамике [11] и в
гидродинамике [12] ; в
гидродинамике она, в частности, отвечает
неустойчивости Кельвина-Гельмгольца. Точки
зарождения ветвей ПМСВ
становится комплексной . Это приводит к
неустойчивости связанных ПМСВ, описываемых
высокочастотными и низкочастотными
участками штриховых кривых. Такого рода
неустойчивость связанных ПМСВ хорошо
известна в электродинамике [11] и в
гидродинамике [12] ; в
гидродинамике она, в частности, отвечает
неустойчивости Кельвина-Гельмгольца. Точки
зарождения ветвей ПМСВ ![]() принадлежат вещественной оси частот, что
свидетельствует [13] о
конвективной (сносовой) природе
неустойчивости ПМСВ на движущейся ДГ.
принадлежат вещественной оси частот, что
свидетельствует [13] о
конвективной (сносовой) природе
неустойчивости ПМСВ на движущейся ДГ.
Для оценки поведения
спектров в окрестности корневых
особенностей принято вводить потери,
присущие реальным системам. Производя в
этой связи замену ![]() в уравнениях (8),(9),(10),
где величина
в уравнениях (8),(9),(10),
где величина ![]() определяет уровень магнитных потерь,
приходим к зависимостям
определяет уровень магнитных потерь,
приходим к зависимостям ![]() , показанных на рис.3,4
жирными линиями. Заметим , что на рис.3
сохранены только те физические ветви
решения, в которые из-за движения и потерь
модифицируются высокочастотные участки
штриховых кривых и которым соответствуют
на рис.4 зависимости с
, показанных на рис.3,4
жирными линиями. Заметим , что на рис.3
сохранены только те физические ветви
решения, в которые из-за движения и потерь
модифицируются высокочастотные участки
штриховых кривых и которым соответствуют
на рис.4 зависимости с ![]() ,
описывающие затухающие магнитостатические
колебания. Замечание [2] о
необходимости отбрасывания спектральной
линии
,
описывающие затухающие магнитостатические
колебания. Замечание [2] о
необходимости отбрасывания спектральной
линии ![]() (рис.3)
получает таким образом физическое
объяснение. При учете движения и потерь
именно она трансформируется в ветвь
решения
(рис.3)
получает таким образом физическое
объяснение. При учете движения и потерь
именно она трансформируется в ветвь
решения ![]() ,
которая соответствует физически
нереализуемым по условию предельного
перехода
,
которая соответствует физически
нереализуемым по условию предельного
перехода ![]() , нарастающим магнитостатическим
колебаниям . Следует отметить , что в
гидродинамике известны гидродинамические
системы (к примеру волны в потоках
стратифицированной жидкости [12]),
для которых имеет обратная ситуация -
нарастающие во времени волны имеют
физический смысл, а затухающие нет.
, нарастающим магнитостатическим
колебаниям . Следует отметить , что в
гидродинамике известны гидродинамические
системы (к примеру волны в потоках
стратифицированной жидкости [12]),
для которых имеет обратная ситуация -
нарастающие во времени волны имеют
физический смысл, а затухающие нет.
Рис.5 Зависимость
групповой скорости ![]() ПМСВ от
ПМСВ от ![]() :
:![]() ;
;
1-![]() ,
2-
,
2-![]() ,
3-
,
3-![]() ,
4-
,
4-![]() ,
5-
,
5-![]() .
.
В феррогранатовых
кристаллах ![]() и при достижимых скоростях
и при достижимых скоростях ![]() см
/ сек корневые особенности
см
/ сек корневые особенности ![]() попадают в магнитостатическую область
волновых чисел
попадают в магнитостатическую область
волновых чисел ![]() .
При этом следует ожидать наиболее
существенных изменений спектра ПМСВ под
влиянием движения ДГ. В частности ,
посредством движения ДГ возможно управлять
задержкой сигнала со спектром ,
приходящимся преимущественно на "спадающую"
часть зависимостей
.
При этом следует ожидать наиболее
существенных изменений спектра ПМСВ под
влиянием движения ДГ. В частности ,
посредством движения ДГ возможно управлять
задержкой сигнала со спектром ,
приходящимся преимущественно на "спадающую"
часть зависимостей ![]() рис.3, где ПМСВ представляет
собой обратную волну. Окрестность корневой
особенности бездиссипативного спектра (8)
ПМСВ на движущейся ДГ интересна еще и тем ,
что именно здесь, согласно (8), масштаб
граничной локализации ПМСВ относительно
геометрических размеров кристалла
наиболее мал. Групповая скорость ПМСВ в
этой окрестности имеет с учетом затухания
ярко выраженный максимум. (см. рис.5 ).
При этом с увеличением скорости ДГ корневая
точка
рис.3, где ПМСВ представляет
собой обратную волну. Окрестность корневой
особенности бездиссипативного спектра (8)
ПМСВ на движущейся ДГ интересна еще и тем ,
что именно здесь, согласно (8), масштаб
граничной локализации ПМСВ относительно
геометрических размеров кристалла
наиболее мал. Групповая скорость ПМСВ в
этой окрестности имеет с учетом затухания
ярко выраженный максимум. (см. рис.5 ).
При этом с увеличением скорости ДГ корневая
точка ![]() и
соответственно максимум групповой
скорости в ее окрестности смещаются в
длинноволновую область спектра.
и
соответственно максимум групповой
скорости в ее окрестности смещаются в
длинноволновую область спектра.
Рис.6 Зависимость
коэффициента ![]() от скорости ДГ -
от скорости ДГ - ![]() :
:
1-![]() , 2-
, 2-![]() ,
3-
,
3-![]() , 4-
, 4-![]() 5-
5-![]() ;
; ![]() .
.
Эффективность параметрического преобразования ПМСВ за счет движения охарактеризуем коэффициентом
где
где
приходящиеся на единицу площади ДГ. Учитывая формулы (12), (13) и отличия в
где
Инвариантность
значений ![]() по отношению к выбору системы отсчета
позволяет говорить о таком же характере
поведения коэффициента
по отношению к выбору системы отсчета
позволяет говорить о таком же характере
поведения коэффициента ![]() и в лабораторной системе отсчета.
и в лабораторной системе отсчета.
Работа выполнена по Проекту А0066 ФЦП "Интеграция".
СПИСОК ЛИТЕРАТУРЫ
1. Вугальтер Г.А., Гилинский И.А. // Изв. ВУЗов. Радиофизика. 1989. Т.32. № 10. С.1187
.2. Гилинский И.А., Минц Р.Г. // ЖЭТФ. 1970. Т.59. Вып.10. С.1230.
3. Сигал М.А.// ЖТФ. 1989. Т.59. Вып.10
. С.137.4. Winter J.M.// Phys. Rev. 1961. Vol.124. P.452.
5. Звездин А.К. , Попков А.Ф.// Письма В ЖЭТФ. 1984. Т.39. Вып.8. С.348.
6. Барьяхтар В.Г., Иванов Б.А., Четкин М.В. // УФН. 1885. Т.146. Вып.3. С.417.
7. Bass F.G., Nasonov N.N., Naumenko O.V. // Phys. Stat. Solidi (b). 1988. Vol.146. N 1. P.61.
8. Потемина Л.Г. // ЖЭТФ. 1986. Т.90. Вып.3. С.964.
9. Филиппов Б.Н., Танкеев А.П. // Динамические эффекты в ферромагнетиках с доменной структурой. М.:Наука, 1987. С.216.
10. Гуревич А.Г. // Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука, 1973. С.592.
11. Лифшиц Е.М., Питаевский Л.П. // Физическая кинетика. М.: Наука, 1979. С.335.
12. Островский Л.А., Рыбак С.А., Цимринг Л.Ш. // УФН. 1986. Т.150. Вып.3. С.417.
13. Ландау Л.Д., Лифшиц Е.М. // Механика сплошных сред. М.: Ростехиздат, 1954. С.141.
Авторы:
Вилков Евгений Александрович, Шевяхов
Николай Сергеевич, e-mail: ufire@MV.ru
Шавров Владимир Григорьевич, e-mail: shavrov@mail.cplire.ru