
| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2001 |  |
КРАЕВАЯ
ЗАДАЧА МАГНИТОСТАТИКИ НА ПЛОСКОСТИ
ДЛЯ СРЕД С КОНЕЧНОЙ МАГНИТНОЙ ПРОНИЦАЕМОСТЬЮ
С.Н. Кузнецов
Северо-Кавказский
государственный технологический университет
Получена 25 октября 2001 г.
В работе поставлена и решена краевая задача магнитостатики на плоскости для конечной относительной магнитной проницаемости среды. В отличие от работ других авторов, граничные условия для магнитного поля были представлены в комплексной форме. Задача была решена в замкнутом виде с применением конформных преобразований и интеграла типа Коши. Показано применение полученных результатов на простейших примерах.
ВВЕДЕНИЕ
В классических работах по теории электромагнитного поля (в частности [1..3]) в основном рассматриваются граничные условия Неймана и Дирихле для уравнений магнитостатики. Решения этих краевых задач были получены в аналитическом или замкнутом виде.
В общем случае для магнитного поля граничные условия формулируются следующим образом:
на
границе раздела магнитных сред для магнитного поля выполняется условие непрерывности
тангенциальной составляющей вектора напряженности магнитного поля - ![]() , [4]:
, [4]:
![]() ,
(1)
,
(1)
для
магнитного поля на границе раздела сред выполняется условие непрерывности
нормальной составляющей вектора магнитной индукции - ![]() [4]:
[4]:
![]() ,
(2)
,
(2)
где "+" и "-" - означают предельные значения на границе раздела сред.
Для таких граничных условий в аналитическом или замкнутом виде решены только простейшие задачи (поле тока расположенного над плоской границей, ограничивающей среду с конечной магнитной проницаемостью; бесконечный полый цилиндр с конечной магнитной проницаемостью в однородном магнитном поле и т.д.).
Поэтому нахождение решения краевой задачи на плоскости для граничных условий (1) и (2) является весьма актуальной задачей.
Широкое применение для решения подобных задач находит теория функций комплексного переменного (ТФКП) [5]. Для того, чтобы воспользоваться методами ТФКП, необходимо представить граничные условия (1) и (2) в комплексной форме записи. Затем решить краевую задачу, используя конформные преобразования и интеграл типа Коши.
Следует отметить, что сама теория функций комплексного переменного и в особенности теория конформных отображений - возникла и развилась на основании физических представлений. А интеграл типа Коши для краевых задач теории аналитических функций комплексного переменного [5], [6] является аналогом потенциалов простого и двойного слоя.
1. ГРАНИЧНЫЕ УСЛОВИЯ В КОМПЛЕКСНОЙ ФОРМЕ
Пусть
имеется контур ![]() , который ограничивает
односвязную область
, который ограничивает
односвязную область ![]() , с относительной
магнитной проницаемостью
, с относительной
магнитной проницаемостью ![]() (рис. 1). Дополнительную
к области
(рис. 1). Дополнительную
к области ![]() часть плоскости
обозначим через
часть плоскости
обозначим через ![]() . Относительная магнитная
проницаемость области
. Относительная магнитная
проницаемость области ![]() равняется единице.
равняется единице.
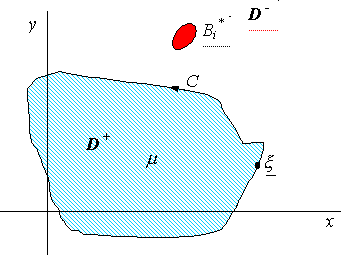
Рис. 1.
Обозначим
через ![]() комплексную магнитную
индукцию, а через
комплексную магнитную
индукцию, а через ![]() комплексно-сопряженную
магнитную индукцию [2], [3], где
комплексно-сопряженную
магнитную индукцию [2], [3], где ![]() - проекция вектора
магнитной индукции на ось x,
- проекция вектора
магнитной индукции на ось x, ![]() - проекция вектора
магнитной индукции на ось y, j- мнимая единица
- проекция вектора
магнитной индукции на ось y, j- мнимая единица ![]() ,
, ![]() -комплексная координата,
-комплексная координата,
![]() сопряженная комплексная
координата ("*"- обозначает сопряженную комплексную величину).
сопряженная комплексная
координата ("*"- обозначает сопряженную комплексную величину).
Комплексный магнитный потенциал можно представить ![]() , где
, где ![]() - действительная
функция комплексного переменного
- действительная
функция комплексного переменного ![]() , которая называется
функцией потока,
, которая называется
функцией потока, ![]() - действительная
функция комплексного переменного
- действительная
функция комплексного переменного ![]() , которая называется
потенциальной функцией.
, которая называется
потенциальной функцией.
Производная
от комплексного магнитного потенциала ![]() умноженная на j,
не что иное, как комплексно-сопряженная магнитная индукция
умноженная на j,
не что иное, как комплексно-сопряженная магнитная индукция ![]() [2], [3]:
[2], [3]:
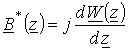 .
.
Перейдем к выводу граничных условий в комплексной форме записи.
Преобразовав
(1), с учетом того, что 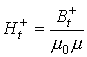 и
и 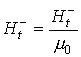 , получим известное
соотношение [1] для тангенциальной составляющей вектора магнитной индукции
, получим известное
соотношение [1] для тангенциальной составляющей вектора магнитной индукции 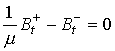 .
.
Представим
вектор магнитной индукции ![]() , как сумму векторов
"источника" магнитного поля
, как сумму векторов
"источника" магнитного поля ![]() и отклика от среды
и отклика от среды
![]() :
:
![]() .
(3)
.
(3)
Под "источниками" будем понимать проводники с постоянным током, электрически заряженные частицы и тела, движущиеся с постоянной скоростью в однородной и изотропной среде, а также намагниченные тела, которые и создают статическое магнитное поле (кавычки применяются потому, что магнитное поле - вихревое).
Для
тангенциальной составляющей вектора ![]() будем иметь
будем иметь ![]() . Тангенциальная
составляющая "источника"
. Тангенциальная
составляющая "источника" ![]() функция непрерывная
везде, кроме некоторых точек принадлежащих области "источника" и поэтому
можно записать
функция непрерывная
везде, кроме некоторых точек принадлежащих области "источника" и поэтому
можно записать
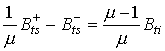 .
(4)
.
(4)
Пусть
![]() - угол наклона касательной
к точке
- угол наклона касательной
к точке ![]() лежащей на границе
раздела магнитных сред,
лежащей на границе
раздела магнитных сред, ![]() - нормальная составляющая
магнитной индукции,
- нормальная составляющая
магнитной индукции, ![]() - тангенциальная
составляющая магнитной индукции,
- тангенциальная
составляющая магнитной индукции, ![]() и
и ![]() - орты,
- орты, ![]() - единичный вектор
нормали,
- единичный вектор
нормали, ![]() - единичный вектор
касательной (рис. 2).
- единичный вектор
касательной (рис. 2).
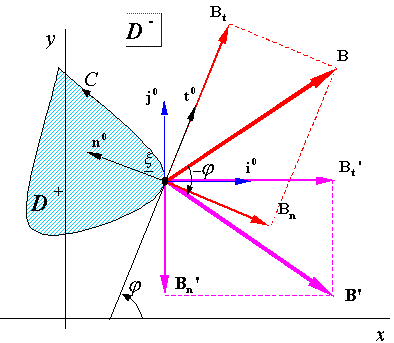
Рис. 2.
Повернем
вектор![]() на угол
на угол ![]() , тогда тангенциальная
составляющая
, тогда тангенциальная
составляющая ![]() также повернется
на угол
также повернется
на угол ![]() и будет параллельна
оси x, а нормальная составляющая
и будет параллельна
оси x, а нормальная составляющая ![]() , после порота будет
параллельна оси y (рис. 2). В комплексной форме поворот на угол
, после порота будет
параллельна оси y (рис. 2). В комплексной форме поворот на угол ![]() , можно представить,
как:
, можно представить,
как:
![]() ,
,
или для сопряженных комплексных величин
![]() .
(5)
.
(5)
Из соотношения (5) для тангенциальной составляющей получим
![]() .
(6)
.
(6)
Тогда подставив (6) в (4), будем иметь
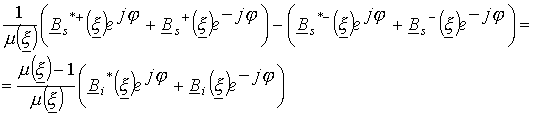 .
.
Умножив
левую и правую часть на ![]() , получим
, получим
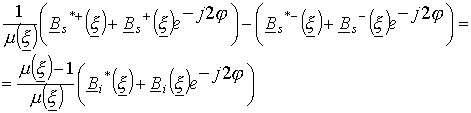 .
.
Дифференциал
![]() комплексно сопряжен
с дифференциалом
комплексно сопряжен
с дифференциалом ![]() , следовательно
, следовательно
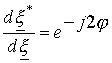 .
(7)
.
(7)
Подставляя
выражение (7) в предыдущее, получим граничное условие для тангенциальной составляющей
![]() в комплексной форме
записи
в комплексной форме
записи
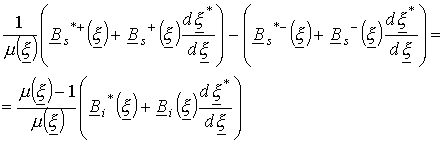 .
(8)
.
(8)
Из выражения (5) для нормальной составляющей, будем иметь
![]() .
(9)
.
(9)
Подставим соотношение (3) в граничное условие (2), затем в полученное выражение подставим (9), имеем
![]() .
.
Умножим
левую и правую часть на ![]() , подставим далее
выражение (7) в полученное, будем иметь граничное условие для нормальной составляющей
, подставим далее
выражение (7) в полученное, будем иметь граничное условие для нормальной составляющей
![]() в комплексной форме
записи
в комплексной форме
записи
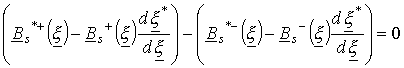 .
(10)
.
(10)
2. ПОСТАНОВКА И РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Краевая задача формулируется следующим образом: найти
функцию ![]() аналитическую в
областях
аналитическую в
областях ![]() и
и ![]() , предельное значение
которой, удовлетворяет на контуре
, предельное значение
которой, удовлетворяет на контуре ![]() (рис. 1) краевому
условию вида (8) и (10).
(рис. 1) краевому
условию вида (8) и (10).
Решение краевой задачи:
Отобразим
область ![]() на нижнюю полуплоскость
при помощи конформного преобразования
на нижнюю полуплоскость
при помощи конформного преобразования ![]() , где
, где ![]() , а
, а ![]() принадлежит нижней
полуплоскости (рис.3).
принадлежит нижней
полуплоскости (рис.3).
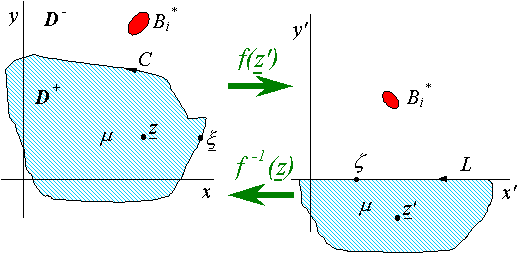
Рис. 3.
Для
точки ![]() принадлежащей контуру
принадлежащей контуру
![]() и точки
и точки ![]() принадлежащей действительной
оси, можно записать
принадлежащей действительной
оси, можно записать ![]() , тогда
, тогда
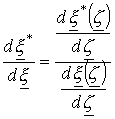 .
(11)
.
(11)
Из выражения для комплексно-сопряженной магнитной индукции будем иметь
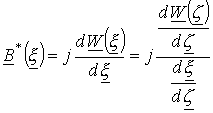 ,
(12)
,
(12)
а для комплексной магнитной индукции
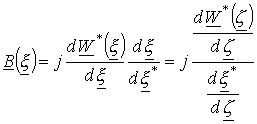 .
(13)
.
(13)
Подставляя соотношения (11), (13) и (13) в граничное условие (8), имеем
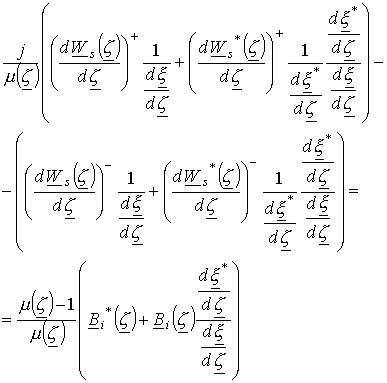 .
.
Производя
несложные преобразования, получим выражение граничного условия для тангенциальной
составляющей ![]() в случае плоской
границы
в случае плоской
границы
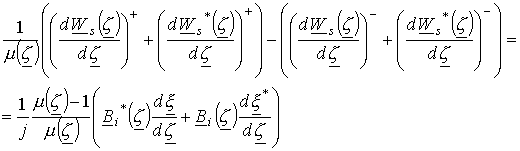 .
(14)
.
(14)
Аналогично
для нормальной составляющей ![]() , граничное условие
в случае плоской границы можно получить из соотношения (10):
, граничное условие
в случае плоской границы можно получить из соотношения (10):
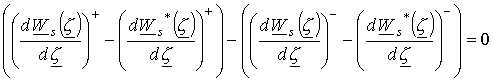 .
(15)
.
(15)
Для нахождения решение краевой задачи для плоской границы будем использовать интеграл типа Коши [5..8] (подобный подход предложен Ф.Д. Гаховым для решения краевой задачи общего типа [7]), в виде которого можно представить производную комплексного магнитного потенциала:
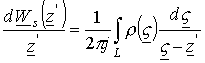 ,
,
где
![]() - плотность, которая
должна удовлетворять условиям Гёльдера, а
- плотность, которая
должна удовлетворять условиям Гёльдера, а ![]() - ядро.
- ядро.
Проинтегрировав
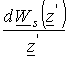 по
по ![]() , получим для комплексного
магнитного потенциала решение в виде
, получим для комплексного
магнитного потенциала решение в виде
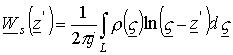 .
(16)
.
(16)
По формуле Сохоцкого [6..8] определим для нижней полуплоскости предельное значение производной комплексного магнитного потенциала в виде
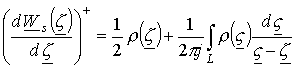 ,
(17)
,
(17)
где
точка ![]() принадлежит границе
между верхней и нижней полуплоскостью (рис. 3).
принадлежит границе
между верхней и нижней полуплоскостью (рис. 3).
Для верхней полуплоскости по формуле Сохоцкого предельное значение производной комплексного магнитного потенциала имеет вид
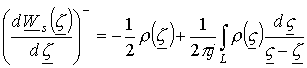 .
(18)
.
(18)
Для
комплексно-сопряженной величины 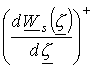 выполняется следующее
соотношение
выполняется следующее
соотношение 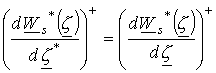 , так как
, так как ![]() , в следствии того,
что точка
, в следствии того,
что точка ![]() лежит на действительной
оси.
лежит на действительной
оси.
Вычтем из выражения (17) сопряженную комплексную величину и получим
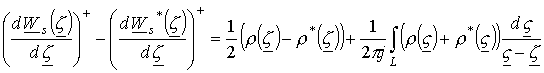 .
.
Вычитая из соотношения (18) сопряженную комплексную величину, будем иметь
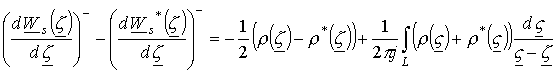 .
.
Вычитая из предыдущего выражения последнее, получим
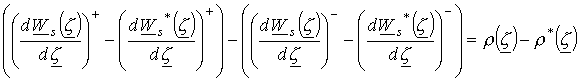
Тогда
исходя из того, что граничное условие (15) равно нулю, следует что ![]() .
.
Сложим с соотношением (17) сопряженную комплексную величину, получим
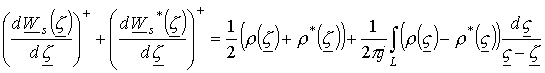 .
.
А с выражением (18) также сложим сопряженную комплексную величину, будем иметь
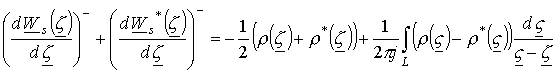 .
.
Интеграл в двух последних выражениях равен нулю, следовательно
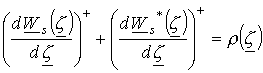
и
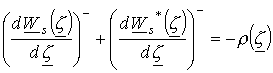 .
.
Подставляя полученные соотношения в граничное условие (14), будем иметь
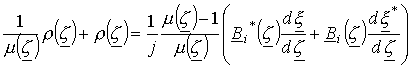 .
.
Делая простые преобразования, получим для плотности следующую формулу
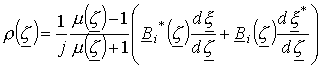 .
(19)
.
(19)
Подставив
формулу для определения плотности (19) в соотношение (16) и прибавляя ![]() , получим выражение
для комплексного магнитного потенциала
, получим выражение
для комплексного магнитного потенциала
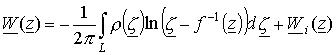 ,
,
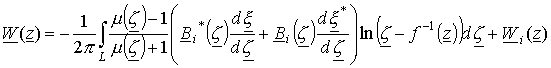 ,
,
где
![]() - контур, ограничивающий
нижнюю полуплоскость и
- контур, ограничивающий
нижнюю полуплоскость и ![]() - конформное преобразование
нижней полуплоскости на область
- конформное преобразование
нижней полуплоскости на область ![]() .
.
Применяя
обратное конформное преобразование ![]() , получим выражение
для комплексного магнитного потенциала
, получим выражение
для комплексного магнитного потенциала
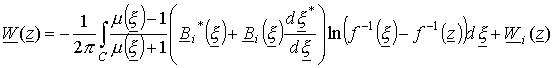 ,
(20)
,
(20)
где
![]() - контур,
ограничивающий область
- контур,
ограничивающий область ![]() . Или используя то,
что
. Или используя то,
что ![]() и
и ![]() , так как
, так как ![]() лежит на действительной
оси, получим другое представление для комплексного магнитного потенциала
лежит на действительной
оси, получим другое представление для комплексного магнитного потенциала
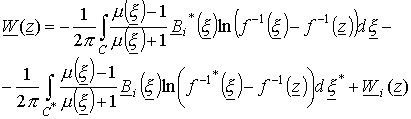 ,
(21)
,
(21)
где
![]() - контур, сопряженный
к контуру
- контур, сопряженный
к контуру ![]() .
.
Дифференцируя комплексный магнитный потенциал (20) и умножая на мнимую единицу, получим решение краевой задачи для комплексно-сопряженной магнитной индукции
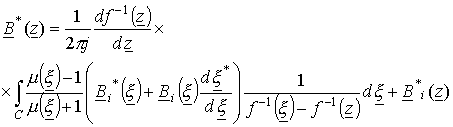 ,
(22)
,
(22)
Аналогично комплексному магнитному потенциалу решение краевой задачи для комплексно-сопряженной магнитной индукции можно представить и в виде
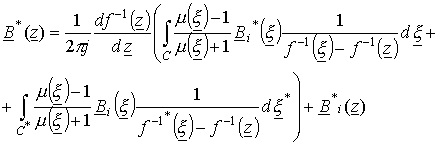 .
(23)
.
(23)
Проверим полученные формулы (22) и (23) для частных случаев.
3. ПРИМЕРЫ
3.1.
Произвольный "источник" магнитного поля ![]() над полуплоскостью
с относительной магнитной проницаемостью
над полуплоскостью
с относительной магнитной проницаемостью ![]() (рис. 4.).
(рис. 4.).
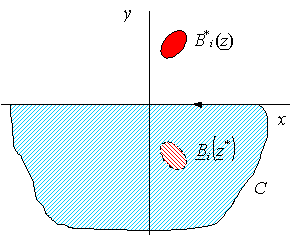
Рис. 4.
Исходя
из формулы (23) и того, что ![]() для среды в виде
нижней полуплоскости имеем
для среды в виде
нижней полуплоскости имеем
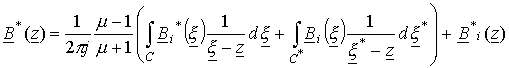 .
.
В
следствии того, что ![]() и
и ![]() аналитические функции
в нижней и верхней полуплоскости соответственно, и непрерывные на границе раздела
сред (на действительной оси) - интегралы в последнем выражении - будут интегралами
Коши.
аналитические функции
в нижней и верхней полуплоскости соответственно, и непрерывные на границе раздела
сред (на действительной оси) - интегралы в последнем выражении - будут интегралами
Коши.
Тогда комплексно-сопряженная магнитная индукция для верхней полуплоскости примет вид:
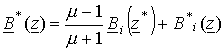 ,
,
то
есть поле будет создаваться двумя "источниками" 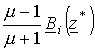 и
и ![]() (рис. 4).
(рис. 4).
Для
нижней полуплоскости поле создается источником 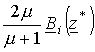 (рис. 4), то есть
(рис. 4), то есть
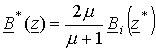 .
.
Таким образом, получены хорошо известные выражения для магнитной индукции, которые получены методом зеркальных изображений [1..3].
3.2.
Произвольный "источник" магнитного поля ![]() над угловой границей
среды с относительной магнитной проницаемостью
над угловой границей
среды с относительной магнитной проницаемостью ![]() (рис. 5).
(рис. 5).
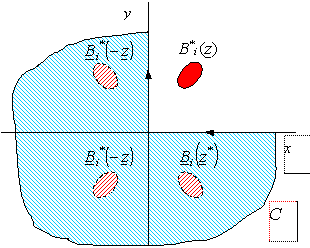
Рис. 5.
Для
среды с границей в виде прямого угла - конформное отображение ![]() и производная
и производная 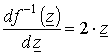 . И тогда из формулы
(23) получим
. И тогда из формулы
(23) получим
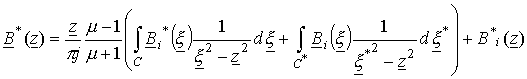
Делая несложные преобразования, имеем
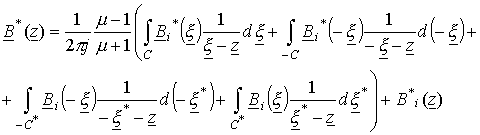 .
.
Поскольку
![]() аналитическая функция
в области ограниченной контуром
аналитическая функция
в области ограниченной контуром ![]() и непрерывна на
этом контуре, первый интеграл в предыдущей формуле - интеграл Коши.
и непрерывна на
этом контуре, первый интеграл в предыдущей формуле - интеграл Коши.
![]() аналитична в области
ограниченной контуром
аналитична в области
ограниченной контуром ![]() и непрерывна на
и непрерывна на
![]() , поэтому и второй
интеграл также будет интегралом Коши.
, поэтому и второй
интеграл также будет интегралом Коши.
Третий
интеграл также является интегралом Коши в следствии того, что ![]() аналитическая функция
в области ограниченной контуром
аналитическая функция
в области ограниченной контуром ![]() и непрерывная функция
на данном контуре.
и непрерывная функция
на данном контуре.
Аналогично
и четвертый интеграл - интеграл Коши из-за аналитичности ![]() в области ограниченной
контуром
в области ограниченной
контуром ![]() и непрерывности
и непрерывности
![]() на контуре
на контуре ![]() .
.
Тогда комплексно-сопряженная магнитная индукция для первого квадранта примет вид:
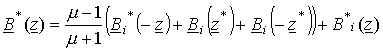 ,
,
для второго квадранта
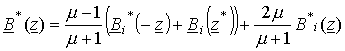 ,
,
для третьего квадранта
 ,
,
и, наконец, для четвертого квадранта
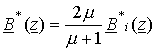 .
.
Метод зеркальных изображений позволяет также получить эти выражения для магнитной индукции [1..3].
3.3.
Произвольный "источник" магнитного поля ![]() над границей в виде
окружности, ограничивающей среду с относительной магнитной проницаемостью
над границей в виде
окружности, ограничивающей среду с относительной магнитной проницаемостью ![]() .
.
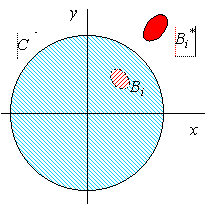
Рис. 6.
Полуплоскость является предельным случаем круга, когда его радиус стремится к бесконечности. Для случая круга формула (23) будет иметь вид
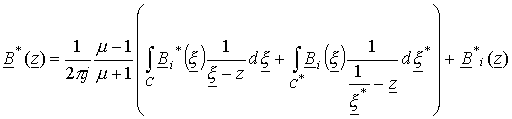 , или
, или
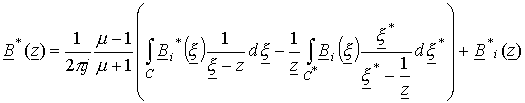 .
.
В
следствии того, что ![]() аналитическая функция
в области ограниченной контуром
аналитическая функция
в области ограниченной контуром ![]() и непрерывна на
этом контуре, первый интеграл в предыдущей формуле - интеграл Коши. Поэтому
внутри круга комплексно-сопряженная магнитная индукция имеет вид:
и непрерывна на
этом контуре, первый интеграл в предыдущей формуле - интеграл Коши. Поэтому
внутри круга комплексно-сопряженная магнитная индукция имеет вид:
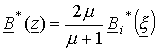 .
.
Для
внешней области ![]() аналитическая функция
непрерывная на контуре
аналитическая функция
непрерывная на контуре ![]() , поэтому второй
интеграл является интегралом Коши. Следовательно вне круга комплексно-сопряженная
магнитная индукция будет имеет вид:
, поэтому второй
интеграл является интегралом Коши. Следовательно вне круга комплексно-сопряженная
магнитная индукция будет имеет вид:
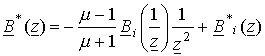 .
.
Подобный результат можно получить методом зеркальных изображений [1..3].
Частным
случаем предыдущего примера является поле тока над цилиндрической средой с относительной
магнитной проницаемостью ![]() . Комплексно-сопряженная
магнитная индукция оси с током
. Комплексно-сопряженная
магнитная индукция оси с током 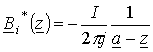 , а комплексная индукция
, а комплексная индукция
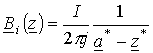 .
.
Вне цилиндрической среды
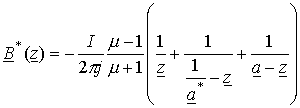 .
.
Внутри среды
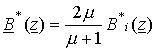 .
.
Приведенные примеры подтверждают правильность полученных выражений (22) и (23).
ЗАКЛЮЧЕНИЕ
В работе поставлена и решена краевая задача магнитостатики на плоскости для конечной магнитной проницаемости среды. Для того, чтобы воспользоваться хорошо разработанным аппаратом теории функций комплексного переменного, граничные условия были представлены в комплексной форме. Применяя конформные преобразования и интеграл типа Коши, было получено решение задачи в замкнутом виде.
Следует отметить, что:
§
решение было получено только для односвязных областей, но его
можно распространить и на многосвязные области,
§
для получения инженерных методик расчета необходимо использовать
приближенные конформные преобразования,
§
полученные результаты легко распространяются и на электростатику.
Решение этих задач и является предметом дальнейших исследований.
ЛИТЕРАТУРА
1. Шимони К. Теоретическая электротехника:
пер. с нем. - М.: Мир, 1964.
2. Бинс К., Лоуренс П. Анализ и расчёт электрических
и магнитных полей. - М.: Энергия, 1970.
3. Бухгольц Г. Расчёт электрических и магнитных полей.
- М.: ИЛ, 1961.
4. Зоммерфельд А. Электродинамика. - М.: ИЛ, 1958.
5. Лаврентьев М.А., Шабат Б.В. Методы теории функций
комплексного переменного. - М.: Наука, 1987.
6. Гахов Ф.Д. Краевые задачи. - М.: Наука,
1977.
7. Гахов Ф.Д. Краевые задачи Римана для
систем n пар функций // Успехи мат. наук. - 1952. - т. VII, вып. 4(50).
8. Смирнов В.И. Курс высшей математики. т. III.- М.:
Наука, 1974.
Автор: С.Н. Кузнецов, к.т.н., с.н.с. Информационного Центра СКГТУ, E-mail: apinf@globalalania.ru