|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2000 |
|
ИНТЕГРАЛ МЕДЛЕННОГО ДВИЖЕНИЯ РЕЛЯТИВИСТСКОГО ЭЛЕКТРОНА В СЛАБОНЕОДНОРОДНОМ ПЕРЕМЕННОМ ПОЛЕ В СЛАБОНЕОДНОРОДНОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЕ
Ю.К.
Алексеев, Ю.Г. Павленко Ю.Г.,
физический
факультет Московского Государственного
университета им. М.В. Ломоносова
Получена 20 января 2000 г.
В работе рассмотрено движение релятивистского электрона в слабонеоднородной параксиальной электромагнитной волне. С использованием гамильтонова формализма и параметризации времени получен адиабатический инвариант медленного движения частицы. Показано, что в сильном поле уменьшается средняя энергия ультрарелятивистского электрона.
Исследование медленного движения релятивистского электрона в слабонеоднородном переменном поле обычно проводится либо с помощью усреднения по явно входящему времени релятивистских уравнений движения [1], либо с помощью ряда замен переменных, исключающих явную зависимость от времени в уравнениях движения, либо в гамильтониане задачи [2]. При этом используется приближение слабого релятивизма, позволяющее существенно упростить математические преобразования и конечные выражения. Однако в ряде случаев представляет интерес точное решение поставленной задачи, единым образом описывающее все предельные случаи. В настоящей работе строится релятивистски-ковариантная теория медленного движения электрона на примере взаимодействия с бегущей слабонеоднородной параксиальной электромагнитной волной.
Зададим поле параксиальной волны
[2,3] вектор-потенциалом ![]() :
:
![]() (1)
(1)
где ![]() и
и ![]() изменяются адиабатически
медленно на расстоянии электронной длины волны. Соответствующий
4-потенциал
изменяются адиабатически
медленно на расстоянии электронной длины волны. Соответствующий
4-потенциал ![]() имеет следующий вид:
имеет следующий вид:
![]() ,
,
где ![]() - фаза волны,
- фаза волны, ![]() ,
, ![]() -
временная координата,
-
временная координата, ![]() ,
, ![]() - волновое число,
- волновое число,
![]() -
координаты волнового вектора.
-
координаты волнового вектора.
Гамильтониан электрона в пространстве Минковского имеет вид:
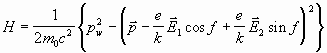 ,
,
где ![]() - 4-импульс электрона.
- 4-импульс электрона. ![]() Проведем ряд канонических преобразований переменных. Используя метод
вариации канонических постоянных и нулевое приближение задачи:
Проведем ряд канонических преобразований переменных. Используя метод
вариации канонических постоянных и нулевое приближение задачи:
![]() ,
,
получаем гамильтониан в следующем виде:
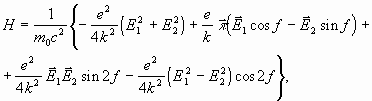
где ![]() - новые переменные.
Используя производящую функцию
- новые переменные.
Используя производящую функцию
![]() ,
,
проведем следующее каноническое преобразование к переменным
![]() , здесь
, здесь ![]() - характерный пролетный угол электронов, определяемый масштабом
неоднородности поля волны. В результате получаем:
- характерный пролетный угол электронов, определяемый масштабом
неоднородности поля волны. В результате получаем:
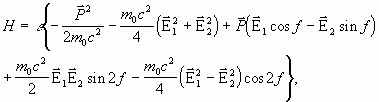
где ![]() ,
, ![]() .
.![]()
Избавившись от
![]() в гамильтониане с помощью замены
в гамильтониане с помощью замены ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
перейдем к медленным переменным
,
перейдем к медленным переменным ![]() ,
используя каноническую теорию усреднения [3]:
,
используя каноническую теорию усреднения [3]:
![]() ,
,
где ![]() - оператор усреднения по явно входящему собственному времени,
- оператор усреднения по явно входящему собственному времени,
![]() - скобки Пуассона,
- скобки Пуассона,
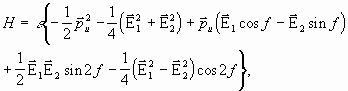 (9)
(9)
![]()
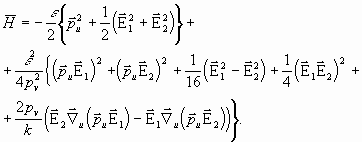 (10)
(10)
Проводя обратные канонические преобразования, получаем
гамильтониан частицы в медленных исходных переменных ![]() :
:
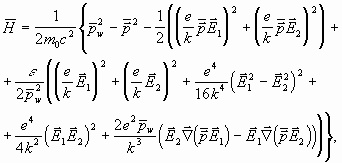 (11)
(11)
где
Рассмотрим первое по ![]() приближение. В трехмерном виде имеем:
приближение. В трехмерном виде имеем:
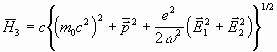 ,
,
здесь ![]() - трехмерный медленный импульс частицы. Отсюда следует, что в
собственном времени сохраняется следующий адиабатический
инвариант:
- трехмерный медленный импульс частицы. Отсюда следует, что в
собственном времени сохраняется следующий адиабатический
инвариант:
![]() .
.
В нерелятивистском приближении (13) переходит в обычный инвариант Гапонова-Миллера [5,6]:
![]()
Рассмотрим ультрарелятивистский случай, когда ![]() .
Используя связь энергии
.
Используя связь энергии ![]() и импульса частицы
и импульса частицы ![]() ,
получаем
,
получаем ![]() , где
, где
![]() - средняя энергия электрона.
Тогда инвариант приобретает форму:
- средняя энергия электрона.
Тогда инвариант приобретает форму:
![]() . (15)
. (15)
Таким образом, в ультрарелятивистском случае, когда его скорость
практически постоянна и равна скорости света, движение
электрона в сильном переменном поле приводит к
уменьшению его средней энергии ![]() .
.
Из (11) следует,
![]() , т.е.
, т.е. ![]() .
С другой стороны, с точностью до
.
С другой стороны, с точностью до ![]()
![]() ,
т.е.
,
т.е. ![]() , где
, где ![]() - собственное время,
- собственное время, ![]() - медленное лабораторное время. Таким образом,
- медленное лабораторное время. Таким образом,
![]() и
и ![]() пропорциональны и в первом приближении по
пропорциональны и в первом приближении по ![]() трехмерный релятивистский инвариант сохраняется в лабораторной системе отсчета.
Для анализа медленного движения с более высокой точностью
по
трехмерный релятивистский инвариант сохраняется в лабораторной системе отсчета.
Для анализа медленного движения с более высокой точностью
по ![]() необходимо использовать параметрическое описание
лабораторного времени на основе четырехмерного инварианта (11).
необходимо использовать параметрическое описание
лабораторного времени на основе четырехмерного инварианта (11).
Преимущество предложенной методики описания медленного движения заряженных частиц в слабонеоднородных быстроосциллирующих полях заключается в том, что использование релятивистски ковариантного гамильтонова формализма позволило строго учесть релятивистские эффекты в задаче, избавившись при этом от неудобных релятивистских радикалов и не прибегая к приближенным их разложениям. Кроме того, параметрическая форма задания лабораторного времени дает дополнительную свободу в описании медленного движения частицы, отсутствующую в трехмерном формализме.
Работа выполнена при поддержке грантов N 96-02-16197 (РФФИ) и N 96-15-97247 (Ведущие научные школы).
Список литературы
1. Schmidt G., Wilcox T. // Physical Review Letters, 1973, v.31, p.1380.
2. Ходжаев К.Ш., Чирков А.Г., Шаталов С.Д. // ЖТФ, 1983, т.53, с.1036.
3. Kogelnik H. and Li T.// Appl. Optics, 1966, v.10, p.1550.
4. Павленко Ю.Г. Гамильтоновы методы в
электродинамике и в квантовой механике.
М., МГУ, 1985, с.336.
5. Гапонов А.В., Миллер М.А. // ЖЭТФ, 1958, т.34, с.242.
6. Миллер М.А. // Изв. ВУЗов. Радиофизика, 1958, т.1, с.110.
Авторы: Алексеев Юрий Константинович,
e-mail: yuka@radp4.phys.msu.su
Павленко Юрий Григорьевич
|
|
|