УДК 621.391.01
АЛГОРИТМЫ НЕКОГЕРЕНТНОГО ПРИЕМА СИГНАЛЬНО-КОДОВЫХ КОНСТРУКЦИЙ НА ОСНОВЕ БЛОКОВЫХ ТУРБО-КОДОВ
Л. Е. Назаров1, П. В. Шишкин2
1ФИРЭ им. В.А.Котельникова РАН, г. Фрязино
2ОАО “Российские космические системы”, г. Москва
Получена 26 июня 2012 г.
Аннотация. Приведены описания и результаты исследований методов некогерентного приема сигнально-кодовых конструкций на основе блоковых турбо-кодов при отсутствии оценок о начальных фазах радиосигналов в приемных устройствах.
Ключевые слова: некогерентный прием, блоковые турбо коды, код Уолша-Адамара.
Abstract. The results of noncoherent decoding algorithm for block turbo codes are presented.
Keywords: noncoherent decoding, block turbo-codes, Walsh-Hadamard codes.
Введение
Проблема разработки методов некогерентного приема сигнально-кодовых конструкций актуальна при создании помехоустойчивых систем связи, для которых процедуры оценивания начальных фаз радиосигналов с использованием устройств фазовой подстройки частоты характеризуются сложностью исполнения и низкой точностью, например, для передачи информации по нестационарным каналам, для систем с псевдослучайной перестройкой рабочей частоты и др. [1].
Известный метод решения
данной задачи основан на каскадной схеме кодирования с использованием алфавита
ортогональных сигналов - используется внешний блоковый помехоустойчивый код и
внутренний ансамбль ортогональных сигналов. Как правило, в качестве внешних
кодов используются коды Рида-Соломона в недвоичных полях, на вход соответствующего
устройства приема поступают «жесткие» (двухуровневые) решения с выхода схемы
обработки сигналов из ансамбля ортогональных сигналов [1]. Примером является система
связи JTIDS (Joint Tactical Information Distribution System) с псевдослучайной перестройкой рабочей частоты,
основу которой составляет внешний код Рида-Соломона над полем ![]() ) с использованием ансамбля
квазиортогональных сигналов объемом
) с использованием ансамбля
квазиортогональных сигналов объемом ![]() .
.
В статье рассматривается схема, использующая в качестве внешнего кода блоковые турбо-коды [2,3]. Данные коды обеспечивают достижение практически предельных вероятностно-энергетических характеристик при умеренной сложности их исполнения средствами цифровой вычислительной техники. Подобная схема исследовалась в работе [4], в которой показана эффективность данной сигнально-кодовой конструкции для решения рассматриваемой задачи. В настоящей статье приведено описание нового алгоритма некогерентного приема данной конструкции, приведены результаты его моделирования и оценки энергетического выигрыша по отношению к исходному алгоритму [4].
Постановка задачи
Рассматривается канал передачи
радиосигналов без памяти, начальная фаза ![]() радиосигналов
полагается случайной величиной с равномерным законом распределения в пределах
радиосигналов
полагается случайной величиной с равномерным законом распределения в пределах ![]() . В канале присутствует белый аддитивный
гауссовский шум с односторонней спектральной плотностью
. В канале присутствует белый аддитивный
гауссовский шум с односторонней спектральной плотностью ![]() .
Используются радиосигналы с двоичной фазовой модуляцией, длительность
элементарных сигналов
.
Используются радиосигналы с двоичной фазовой модуляцией, длительность
элементарных сигналов ![]() .
.
На рис.1 приведена блок-схема формирования исследуемой сигнально-кодовой конструкции.
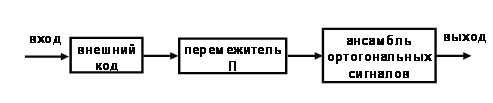
Рис.1 Блок-схема формирования сигнально-кодовой конструкции.
В качестве внешнего кода
используется блоковый турбо-код. Кодовые слова блоковых турбо-кодов формируются
на основе двух двоичных блоковых кодов ![]() (
(![]() ) и
) и ![]() (
(![]() ) и эквивалентны двумерной матрице
размером
) и эквивалентны двумерной матрице
размером ![]() . Строки матрицы - кодовые слова кода
. Строки матрицы - кодовые слова кода ![]() , столбцы матрицы - кодовые слова кода
, столбцы матрицы - кодовые слова кода ![]() [2]. Здесь
[2]. Здесь ![]() ,
, ![]() - длительность кодовых слов и размерность
блокового кода. Длительность кодовых слов турбо-кода равна
- длительность кодовых слов и размерность
блокового кода. Длительность кодовых слов турбо-кода равна ![]() , размерность
, размерность ![]() ,
кодовая скорость
,
кодовая скорость ![]() . Если составляющие блоковые
коды систематические, то информационные символы кода-произведения образуют
прямоугольную матрицу размером
. Если составляющие блоковые
коды систематические, то информационные символы кода-произведения образуют
прямоугольную матрицу размером ![]() в составе двумерной
матрицы кодовых слов.
в составе двумерной
матрицы кодовых слов.
С выхода перемежителя П
объемом ![]() последовательность кодовых символов
разбивается на
последовательность кодовых символов
разбивается на ![]() последовательностей
длительностью
последовательностей
длительностью ![]() , поступающих на вход устройства
формирования ортогональных сигналов, в качестве которых используется ансамбль
функций Уолша объемом
, поступающих на вход устройства
формирования ортогональных сигналов, в качестве которых используется ансамбль
функций Уолша объемом ![]() .
.
Пусть ![]() ,
, ![]() -
прямая и квадратурная дискретные реализации с выхода демодулятора
-
прямая и квадратурная дискретные реализации с выхода демодулятора
![]() , (1)
, (1)
![]() . (2)
. (2)
Здесь ![]() -
символы (
-
символы (![]() ) переданной функции Уолша с номером
) переданной функции Уолша с номером ![]() (
(![]() ),
), ![]() - амплитуда радиосигналов на входе
приемного устройства,
- амплитуда радиосигналов на входе
приемного устройства, ![]() - помеховые составляющие,
статистически независимые, имеющие гауссовский закон распределения с нулевыми
средними и с дисперсиями
- помеховые составляющие,
статистически независимые, имеющие гауссовский закон распределения с нулевыми
средними и с дисперсиями ![]() .
.
Разработка вычислительной
процедуры обработки реализаций ![]() ,
, ![]() при некогерентном приеме сигналов
составляет суть задачи.
при некогерентном приеме сигналов
составляет суть задачи.
Алгоритмы некогерентного приема
Процедура обработки
реализаций ![]() ,
, ![]() при
некогерентном приеме сигналов состоит из двух этапов [4].
при
некогерентном приеме сигналов состоит из двух этапов [4].
На первом этапе вычисляются
“мягкие” решения 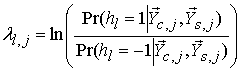 для декодера блокового
турбо-кода. Апостериорные вероятности
для декодера блокового
турбо-кода. Апостериорные вероятности ![]() вычисляются
по правилу
вычисляются
по правилу
![]() (3)
(3)
Здесь ![]() -
символ Кронекера;
-
символ Кронекера; ![]() . Обозначение
. Обозначение ![]() соответствует усредненной по
соответствует усредненной по ![]() условной вероятности функции Уолша
условной вероятности функции Уолша ![]() длительностью
длительностью ![]()
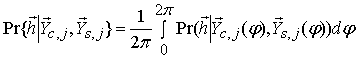 .
.
Для вероятности ![]() формула Байеса имеет вид
формула Байеса имеет вид 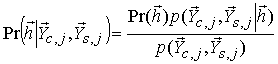 ,
, ![]() .
.
Для функции правдоподобия
![]() после усреднения по
после усреднения по ![]() получаем результирующее соотношение
получаем результирующее соотношение
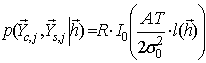 ,
, ![]() , (4)
, (4)
здесь ![]() -
функция Бесселя 0-го порядка,
-
функция Бесселя 0-го порядка, ![]() - постоянный
множитель;
- постоянный
множитель; 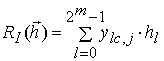 ;
; 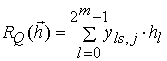 .
.
Таким образом, процедура
оценки апостериорных вероятностей ![]() заключается в
вычислении корреляций
заключается в
вычислении корреляций ![]() , их нелинейном преобразовании в
соответствии с (4) и суммировании (3).
, их нелинейном преобразовании в
соответствии с (4) и суммировании (3).
Вычисление ![]() и суммы (3) может быть осуществлено при
помощи алгоритма быстрого преобразования Уолша размерностью
и суммы (3) может быть осуществлено при
помощи алгоритма быстрого преобразования Уолша размерностью ![]() с базовыми операциями “сложение-вычитание-пересылки”,
что повышает производительность по отношению к прямому вычислению в
с базовыми операциями “сложение-вычитание-пересылки”,
что повышает производительность по отношению к прямому вычислению в ![]() раз [4,5].
раз [4,5].
Более простой метод вычисления
мягких решений ![]() , не требующий знания
энергетических параметров канала
, не требующий знания
энергетических параметров канала ![]() и
и ![]() , основан на применении приближенного соотношения
[3]
, основан на применении приближенного соотношения
[3]
![]() . (5)
. (5)
При вычислении
соотношения (5) можно применить модифицированный алгоритм быстрого
преобразования Уолша размерностью ![]() с базовыми операциями “сравнение-пересылки” [6]. На рис.2 приведена схема основного
элемента модифицированного алгоритма быстрого преобразования Уолша.
с базовыми операциями “сравнение-пересылки” [6]. На рис.2 приведена схема основного
элемента модифицированного алгоритма быстрого преобразования Уолша.
В результате выполнении
первого этапа вычисляются “мягкие” решения ![]() ,
, ![]() ,
, ![]() ,
образующие двумерную матрицу
,
образующие двумерную матрицу ![]() , соответствующую двумерным кодовым словам
блокового турбо-кода.
, соответствующую двумерным кодовым словам
блокового турбо-кода.
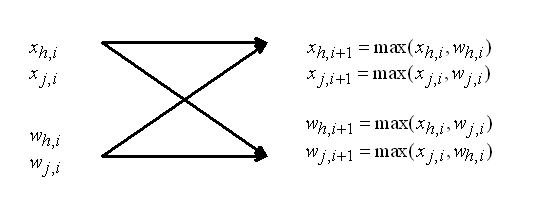
Рис.2. Схематическое изображение базового элемента модифицированного алгоритма быстрого преобразования Уолша с операциями “сравнение-пересылки”.
На втором этапе реализуется
алгоритм итеративного приема с использованием “мягких” решений ![]() . Пусть
. Пусть ![]() -
информационные символы, образующие матрицу в двумерной матрице
-
информационные символы, образующие матрицу в двумерной матрице ![]() блокового турбо-кода;
блокового турбо-кода; 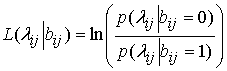 - отношение правдоподобия условных
плотностей вероятностей отсчетов
- отношение правдоподобия условных
плотностей вероятностей отсчетов ![]() ;
; 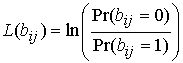 - отношение априорных символьных
вероятностей.
- отношение априорных символьных
вероятностей.
Алгоритм приема блоковых
турбо-кодов является итеративным, итерация содержит два шага [3]. На первом
шаге ![]() -ой итерации вычисляются приращения
отношений апостериорных вероятностей
-ой итерации вычисляются приращения
отношений апостериорных вероятностей ![]() для кодовых символов
для кодовых символов ![]() для
для ![]() -го
кодового слова
-го
кодового слова ![]() блокового кода
блокового кода ![]()
![]() . (6)
. (6)
Здесь 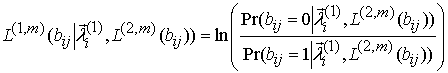 ;
; ![]() - реализация в составе
- реализация в составе ![]() , соответствующая кодовому слову
, соответствующая кодовому слову ![]() . Для первой итерации (
. Для первой итерации (![]() ) верно условие
) верно условие ![]() .
.
На втором шаге ![]() -ой итерации подобные вычисления
производятся для вычисления приращения апостериорных символьных вероятностей
кодовых слов
-ой итерации подобные вычисления
производятся для вычисления приращения апостериорных символьных вероятностей
кодовых слов ![]() кода
кода ![]()
![]() . (7)
. (7)
Здесь ![]() - реализация в составе
- реализация в составе ![]() , соответствующая кодовому слову
, соответствующая кодовому слову ![]() . Величины
. Величины ![]() используются
в качестве априорной информации для первого шага последующей (
используются
в качестве априорной информации для первого шага последующей (![]() )-ой итерации, то есть
)-ой итерации, то есть ![]() .
.
На последней итерации
принимаются решения относительно символов ![]() : при
условии
: при
условии ![]() полагается
полагается ![]() , иначе
, иначе
![]() .
.
При вычислении величин ![]() ,
, ![]() применяется
алгоритм подоптимальной оценки [3]
применяется
алгоритм подоптимальной оценки [3]
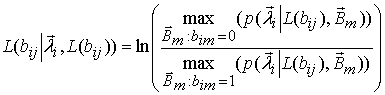 . (8)
. (8)
Процедура поиска кодовых
векторов ![]() , определяющих максимумы делимого и
делителя в (8), основана на использовании алгоритма Чейза [3]. Алгоритм Чейза
не требует оценки энергетических параметров канала передачи.
, определяющих максимумы делимого и
делителя в (8), основана на использовании алгоритма Чейза [3]. Алгоритм Чейза
не требует оценки энергетических параметров канала передачи.
Модификация изложенного алгоритма некогерентного приема (5)-(8) определяет дополнительный энергетический выигрыш. Суть модификации алгоритма - применение итеративной обработки, производимой в сочетании двух приведенных этапов.
Блок-схема результирующего алгоритма приведена на рис.3. Алгоритм включает выполнение двух этапов.
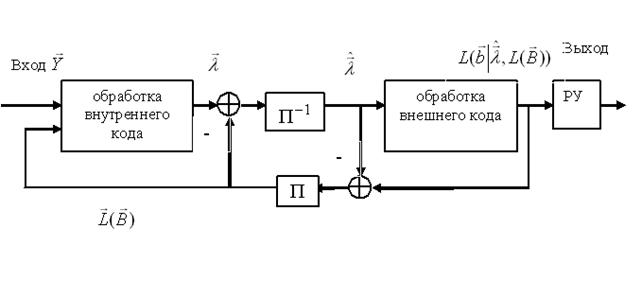
Рис.3. Блок-схема результирующего алгоритма некогерентного приема (РУ - решающее устройство).
На первом этапе вычисляются
мягкие решения, используя вычисленные значения ![]() с использованием
входных реализаций
с использованием
входных реализаций ![]() ,
, ![]() и априорной
информации
и априорной
информации ![]() относительно функций Уолша
относительно функций Уолша ![]() , поступающей с выхода блока обработки
внешнего кода,
, поступающей с выхода блока обработки
внешнего кода,
![]() . (9)
. (9)
На устройство обработки внешнего
блокового турбо-кода поступают величины ![]() с
выхода перемежителя
с
выхода перемежителя ![]() .
.
На втором этапе устройство
обработки внешнего блокового турбо-кода вычисляет приращения апостериорных символьных вероятностей
кодовых слов турбо-кода ![]() , которые после перемежения поступают на
устройство обработки внутреннего кода (функций Уолша).
, которые после перемежения поступают на
устройство обработки внутреннего кода (функций Уолша).
Решающим устройством
после выполнения задаваемого количества итераций принимается решение
относительно кодовых символов
![]() , правило решения совпадает с приведенным
правилом для блокового турбо-кода на втором этапе алгоритма некогерентного
приема.
, правило решения совпадает с приведенным
правилом для блокового турбо-кода на втором этапе алгоритма некогерентного
приема.
Результаты моделирования
На рис. 4 приведены
вероятности ошибки на бит ![]() для сигнально-кодовой
конструкции на основе блокового турбо-кода (1024,441) и ансамбля функций Уолша
объемом 64. По оси абсцисс отложены значения сигнал/помеха
для сигнально-кодовой
конструкции на основе блокового турбо-кода (1024,441) и ансамбля функций Уолша
объемом 64. По оси абсцисс отложены значения сигнал/помеха ![]() , здесь
, здесь ![]() -
энергия на бит. Кривая 1 соответствует применению исходного алгоритма
некогерентного приема, кривая 2 соответствует применению модифицированного
алгоритма итеративного некогерентного приема (5 итераций). Данные кривые
получены путем компьютерного моделирования приведенного модифицированного
алгоритма некогерентного приема. Энергетический выигрыш кривой 2 по отношению к
кривой 1 достигает 0.3 дБ.
-
энергия на бит. Кривая 1 соответствует применению исходного алгоритма
некогерентного приема, кривая 2 соответствует применению модифицированного
алгоритма итеративного некогерентного приема (5 итераций). Данные кривые
получены путем компьютерного моделирования приведенного модифицированного
алгоритма некогерентного приема. Энергетический выигрыш кривой 2 по отношению к
кривой 1 достигает 0.3 дБ.
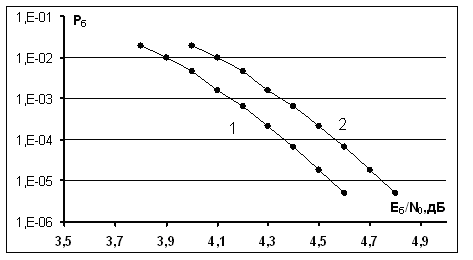
Рис. 4. Вероятности ошибки для сигнально-кодовой конструкции на основе блокового турбо-кода (1024,441) и ансамбля функций Уолша объемом 64: 1 - применение исходного алгоритма некогерентного приема; 2 - применение модифицированного алгоритма некогерентного приема.
На рис. 5 приведены
вероятности ошибки на бит ![]() для ряда
рассматриваемых сигнально-кодовых конструкции на основе блоковых турбо-кода и
кодов Рида-Соломона [3]. Кривая 1 и кривая 2 соответствуют сигнально-кодовым
конструкциям на основе кода Рида-Соломона (63,47) над полем
для ряда
рассматриваемых сигнально-кодовых конструкции на основе блоковых турбо-кода и
кодов Рида-Соломона [3]. Кривая 1 и кривая 2 соответствуют сигнально-кодовым
конструкциям на основе кода Рида-Соломона (63,47) над полем ![]() и турбо-кода (4096,2601) и ансамбля
функций Уолша объемом 64. Кодовые скорости кода Рида-Соломона и блокового
турбо-кода близки (
и турбо-кода (4096,2601) и ансамбля
функций Уолша объемом 64. Кодовые скорости кода Рида-Соломона и блокового
турбо-кода близки (![]() ). Данные кривые получены путем
компьютерного моделирования приведенного модифицированного итеративного алгоритма
некогерентного приема (5 итераций). Видно, что энергетический выигрыш кривой 2
по отношению к кривой 1 для значения
). Данные кривые получены путем
компьютерного моделирования приведенного модифицированного итеративного алгоритма
некогерентного приема (5 итераций). Видно, что энергетический выигрыш кривой 2
по отношению к кривой 1 для значения ![]() достигает 1.75 дБ. При
уменьшении вероятности
достигает 1.75 дБ. При
уменьшении вероятности ![]() значения энергетического выигрыша
увеличиваются.
значения энергетического выигрыша
увеличиваются.
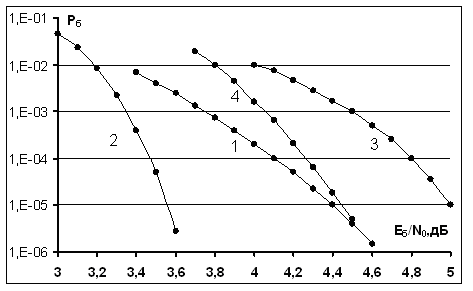
Рис. 5. Вероятностные кривые для
сигнально-кодовых конструкции на основе блоковых турбо-кода и кодов
Рида-Соломона: 1 - на основе кода Рида-Соломона (63,47) над полем ![]() и ансамбля функций Уолша объемом 64; 2 -
на основе турбо-кода (4096,2601) и ансамбля функций Уолша объемом 64; 3 - на
основе кода Рида-Соломона (63,31) над полем
и ансамбля функций Уолша объемом 64; 2 -
на основе турбо-кода (4096,2601) и ансамбля функций Уолша объемом 64; 3 - на
основе кода Рида-Соломона (63,31) над полем ![]() и
ансамбля функций Уолша объемом 64; 4 - на основе турбо-кода (1024,441) и
ансамбля функций Уолша объемом 64.
и
ансамбля функций Уолша объемом 64; 4 - на основе турбо-кода (1024,441) и
ансамбля функций Уолша объемом 64.
Кривые 3 и 4 на рис.5
соответствуют сигнально-кодовым конструкциям на основе кода Рида-Соломона (63,31)
над полем ![]() и турбо-кода (1024,441) и ансамбля
функций Уолша объемом 64. Кодовые скорости кода Рида-Соломона и турбо-кода
близки (
и турбо-кода (1024,441) и ансамбля
функций Уолша объемом 64. Кодовые скорости кода Рида-Соломона и турбо-кода
близки (![]() ). Видно, что энергетический выигрыш
кривой 2 по отношению к кривой 1 для
). Видно, что энергетический выигрыш
кривой 2 по отношению к кривой 1 для ![]() достигает 1.6 дБ.
достигает 1.6 дБ.
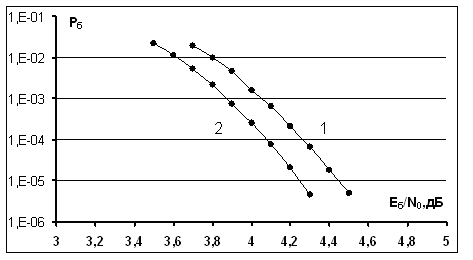
Рис. 6. Вероятностные кривые для сигнально-кодовой конструкции на основе турбо-кода (1024,441) и ансамбля функций Уолша объемом 64: 1 - исходный алгоритм некогерентного приема; 2 - модифицированный алгоритм некогерентного приема.
На рис. 6 приведены
вероятности ![]() для сигнально-кодовой конструкции на основе
турбо-кода (1024,441) и ансамбля функций Уолша объемом 64. Кривые 1 и 2
получены путем компьютерного моделирования исходного и модифицированного
алгоритмов некогерентного приема (5 итераций). Видно, что при применении
модифицированного алгоритма приема энергетический выигрыш по отношению к
исходному алгоритму некогерентного приема достигает 0.3 дБ.
для сигнально-кодовой конструкции на основе
турбо-кода (1024,441) и ансамбля функций Уолша объемом 64. Кривые 1 и 2
получены путем компьютерного моделирования исходного и модифицированного
алгоритмов некогерентного приема (5 итераций). Видно, что при применении
модифицированного алгоритма приема энергетический выигрыш по отношению к
исходному алгоритму некогерентного приема достигает 0.3 дБ.
Заключение
Приведено описание нового алгоритма итеративного некогерентного приема сигнально-кодовых конструкций на основе блоковых турбо-кодов и ансамблей ортогональных сигналов, соответствующих функциям Уолша. Путем компьютерного моделирования данного алгоритма для ряда конструкций показано наличие энергетического выигрыша по отношению к подобной сигнально-кодовым конструкциям на основе кодов Рида-Соломона и по отношению к известному алгоритму некогерентного приема.
Литература
1. Кларк Дж. мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. Перевод с англ. М.: Радио и связь. 1987. 392 с.
2. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Перевод с англ. М.: Техносфера. 2005. 320 с.
3. Pyndiah R.M. Near-optimum decoding of product-codes: block turbo-codes. //IEEE Transactions on Communication. 1998. V.46. N8. P.1003-1010.
4. Назаров Л.Е Итеративный некогерентный прием турбо-кодов на основе двоичных блоковых кодов. // Радиотехника и электроника. 2005. Т.50. №3 Стр.315-320.
5. Ахмед Н., Рао К.Р. Ортогональные преобразования при цифровой обработке сигналов. М.:Связь. 1980. 248 с.
6. Назаров Л.Е. Алгоритмы посимвольного приема сигналов.// Информационные технологии. 2010. №2. Стр.53-55.