|
Часть 3 |
3. Разработка методов повышения чувствительности голографического коррелятора
Проведенные нами исследования позволили установить, что путем преобразования информации либо во входной [7], либо в частотной плоскости коррелятора [8] удается существенно повысить чувствительность систем контроля. При этом для деталей малых размеров (менее 5 мм) с практической точки зрения оптимальным является преобразование информации в частотной плоскости, а для деталей с размерами более 5 мм — преобразование информации в предметной плоскости. Рассмотрим каждый из отмеченных случаев.
3.1. Преобразование информации в частотной плоскости коррелятора
Как известно [4], передаточная характеристика согласованного фильтра в общем виде описывается как
где ![]() — комплексно сопряженный спектр
эталонного сигнала;
— комплексно сопряженный спектр
эталонного сигнала;![]() — дополнительная фильтрующая функция;
— дополнительная фильтрующая функция; ![]() — функция зрачка [
— функция зрачка [![]() в пределах полосы пропускания фильтра и
в пределах полосы пропускания фильтра и ![]() вне поло сы]. Постоянный коэффициент
вне поло сы]. Постоянный коэффициент ![]() выбирается из условия, что
выбирается из условия, что ![]() .
.
Из выражения (8) видно,
что правильный выбор фильтрующей функции ![]() позволяет регулировать дискриминационные
возможности передаточной характеристики
фильтра
позволяет регулировать дискриминационные
возможности передаточной характеристики
фильтра ![]() .
Синтез фильтрующей функции
.
Синтез фильтрующей функции ![]() представляет собой довольно сложную
техническую проблему, так как в общем
случае функция
представляет собой довольно сложную
техническую проблему, так как в общем
случае функция ![]() должна быть комплексной. Однако для бинарных
сигналов, имеющих место при решении задач
автоматического контроля геометрии
деталей, проблема синтеза моделирующей
функции
должна быть комплексной. Однако для бинарных
сигналов, имеющих место при решении задач
автоматического контроля геометрии
деталей, проблема синтеза моделирующей
функции ![]() существенно упрощается. Объясняется это
тем, что детали состоят лишь из
пропускающих и не пропускающих свет
областей. В результате получается спектр
пространственных частот, имеющий высокую
интенсивность на низких частотах и очень
малую, но не исчезающую интенсивность на
высоких частотах. Последнее обстоятельство
и явилось причиной для
рассмотрения вопроса по увеличению
чувствительности голографического
коррелятора.
существенно упрощается. Объясняется это
тем, что детали состоят лишь из
пропускающих и не пропускающих свет
областей. В результате получается спектр
пространственных частот, имеющий высокую
интенсивность на низких частотах и очень
малую, но не исчезающую интенсивность на
высоких частотах. Последнее обстоятельство
и явилось причиной для
рассмотрения вопроса по увеличению
чувствительности голографического
коррелятора.
Действительно, пусть на входе голографического коррелятора находится деталь в виде прямоугольного отверстия с функцией пропускания
![]() ,
,
где ![]() — отклонение размера от эталона в
направлении оси X. Для согласованного
фильтра на эталонную деталь с откликом
— отклонение размера от эталона в
направлении оси X. Для согласованного
фильтра на эталонную деталь с откликом
![]()
и ![]() находим, что корреляционный отклик на входе
коррелятора
находим, что корреляционный отклик на входе
коррелятора
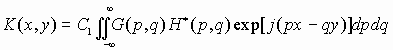
будет равен
Поскольку входной сигнал
является действительной функцией, то для
обработки можно использовать половину
спектра пространственных частот. Кроме
того, положив ![]() и вводя пределы интегрирования
и вводя пределы интегрирования ![]() и
и ![]() ,
выражение (9) можно записать как
,
выражение (9) можно записать как
После интегрирования получим
где ![]() —
интегральный синус.
—
интегральный синус.
Хотя выражение (11) и
дает полное аналитическое решение
выражения (10), требуемое
соотношение между главным значением ![]() и пределами интегрирования
и пределами интегрирования ![]() и
и ![]() здесь
найти весьма нелегко. Однако для
ограниченного интервала отклонения
здесь
найти весьма нелегко. Однако для
ограниченного интервала отклонения ![]() ,
лежащего в диапазоне
,
лежащего в диапазоне ![]() ,
где
,
где ![]() ,
оптимизация достигается путем разложения в
ряд выражения (10). С этой целью видоизменим
запись выражения (10) и разложим в
ряд члены с
,
оптимизация достигается путем разложения в
ряд выражения (10). С этой целью видоизменим
запись выражения (10) и разложим в
ряд члены с ![]() и
и ![]() .
Тогда будем иметь
.
Тогда будем иметь
![]()
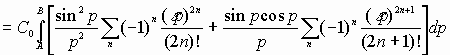
или окончательно получим, что
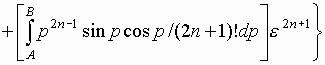 .
(12)
.
(12)
Так как выходной сигнал фотоприемника пропорционален интенсивности корреляционного отклика, то нас интересует поведение функции
где  .
.
Видно, что для исследования
поведения корреляционного отклика от
изменения отклонения ![]() необходимо знание коэффициентов
необходимо знание коэффициентов ![]() .
С учетом выражения (12)
.
С учетом выражения (12) ![]() — коэффициент разложения для
— коэффициент разложения для ![]() имеет вид
имеет вид
 .
(14)
.
(14)
Подставив (14) в (13)
найдем, что аналитическое выражение для
коэффициента ![]() запишется как
запишется как
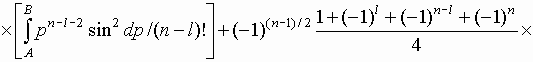
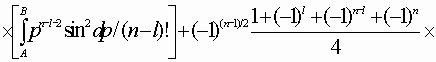
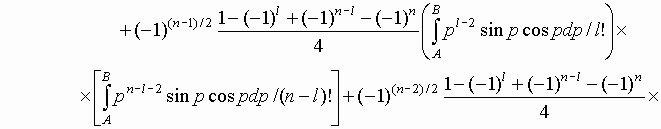
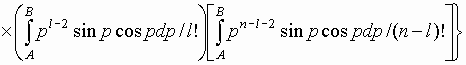
![]() .
(15)
.
(15)
Численное решение для
нормированного корреляционного отклика ![]() вплоть до члена пятого порядка показало,
что ряд быстро сходится внутри интервала
вплоть до члена пятого порядка показало,
что ряд быстро сходится внутри интервала ![]() .
.
Рассмотрим аппроксимацию третьего порядка, как представляющую практический интерес. Аппроксимация третьего порядка корреляционного отклика имеет вид
где с учетом выражения (15)
первые четыре коэффициента ![]() ,
,
![]() ,
, ![]() ,
,
![]() описываются как
описываются как
Из анализа выражений (17, 18, 19, 20) можно сделать следующее заключение.
Член ![]() представляет собой интенсивность
автокорреляционного сигнала, причем он
соответствует уровню интенсивности в
интервале отклонений
представляет собой интенсивность
автокорреляционного сигнала, причем он
соответствует уровню интенсивности в
интервале отклонений ![]() .
Для приемлемой производительности
обработки информации коррелятора
необходимо определить значения величин
.
Для приемлемой производительности
обработки информации коррелятора
необходимо определить значения величин ![]() и
и ![]() ,
которые находились бы в пределах
экспериментальных ограничений и давали бы
максимальное значение коэффициента
,
которые находились бы в пределах
экспериментальных ограничений и давали бы
максимальное значение коэффициента ![]() .
Для повышения точностных возможностей
коррелятора необходимо провести
оптимизацию отклика так, чтобы градиент
.
Для повышения точностных возможностей
коррелятора необходимо провести
оптимизацию отклика так, чтобы градиент ![]() стал наибольшим. При этом
коррелятор, предназначенный для
разбраковки изделий, должен иметь линейный
корреляционный отклик в интервале
требуемых отклонений. Этого можно
достигнуть применением дополнительного
фильтра
стал наибольшим. При этом
коррелятор, предназначенный для
разбраковки изделий, должен иметь линейный
корреляционный отклик в интервале
требуемых отклонений. Этого можно
достигнуть применением дополнительного
фильтра ![]() ,
который должен усиливать коэффициент
,
который должен усиливать коэффициент ![]() и ослаблять коэффициенты
и ослаблять коэффициенты ![]() и
и ![]() .
Усиление коэффициента
.
Усиление коэффициента ![]() можно получить за счет использования либо
линейного амплитудного
фильтра
можно получить за счет использования либо
линейного амплитудного
фильтра ![]() ,
пропускающего любую положительную или
отрицательную часть подинтегрального
выражения
,
пропускающего любую положительную или
отрицательную часть подинтегрального
выражения ![]() (соотношения (18)), либо линейного
фазового фильтра
(соотношения (18)), либо линейного
фазового фильтра ![]() ,
обеспечивающего задержку фазы на
,
обеспечивающего задержку фазы на ![]() относительно соседнего экстремума.
относительно соседнего экстремума.
Отметим невозможность полного
подавления коэффициентов высших порядков
из-за того, что подинтегральные выражения
всех нечетных коэффициентов являются
осциллирующими по фазе функциями [выр. (14,
17-20)] и любое усиление
коэффициента ![]() приводит к усилению коэффициентов вида
приводит к усилению коэффициентов вида ![]() .
Сказанное поясняется рис.3. Из
него видно, что фазовый линейный фильтр
.
Сказанное поясняется рис.3. Из
него видно, что фазовый линейный фильтр ![]() можно рассматривать в качестве
оптимального, поскольку он работает как
минимизирующий линейный фильтр, полностью
подавляя часть
можно рассматривать в качестве
оптимального, поскольку он работает как
минимизирующий линейный фильтр, полностью
подавляя часть 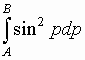 коэффициента
коэффициента ![]() .
.
|
Рис.3. Пояснение к принципу действия дополнительных фильтров: (- ¾
¾ ¾ )
член нулевого порядка,
|
Для обеспечения допусков при
разбраковке изделий коррелятор должен
иметь гладкую выходную характеристику и
должен быть связан с пороговой схемой. В
частности, такую разбраковку изделий
обеспечивает отклик коррелятора с
квадратичной характеристикой. Достигается
это за счет применения дополнительного
фильтра ![]() ,
который должен минимизировать
одновременно коэффициенты
,
который должен минимизировать
одновременно коэффициенты ![]() и
и ![]() .
.
Так как среднее значение
основной части коэффициента ![]() меньше
меньше 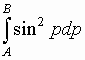 ,
но больше
,
но больше ![]() ,
то любое расширение полосы пропускания
приводит к увеличению чувствительности
коррелятора. Другими словами, оптимальным
фильтром
,
то любое расширение полосы пропускания
приводит к увеличению чувствительности
коррелятора. Другими словами, оптимальным
фильтром ![]() будет являться полосовой фильтр,
обеспечивающий максимальную полосу
пропускания и подавляющий коэффициенты
будет являться полосовой фильтр,
обеспечивающий максимальную полосу
пропускания и подавляющий коэффициенты ![]() и
и ![]() .
.
Для нахождения предельных
значений ![]() и
и ![]() дополнительных фильтров
дополнительных фильтров ![]() и
и ![]() была
проведена количественная оценка выражений
(18) и (16) с привлечением
ЭВМ. Аппроксимация пятого порядка
выходного сигнала
была
проведена количественная оценка выражений
(18) и (16) с привлечением
ЭВМ. Аппроксимация пятого порядка
выходного сигнала ![]() проводилась путем изменения параметров
проводилась путем изменения параметров ![]() и
и ![]() в
интервале от
в
интервале от ![]() до
до ![]() соответственно для области отклонений
соответственно для области отклонений ![]() .
Полученные результаты показали быструю
сходимость ряда внутри указанного
интервала для обоих типов дополнительных
фильтров, работающих с четырьмя
максимумами пространственного спектра
частот. Поскольку, как было отмечено выше,
фазоинверсный фильтр
.
Полученные результаты показали быструю
сходимость ряда внутри указанного
интервала для обоих типов дополнительных
фильтров, работающих с четырьмя
максимумами пространственного спектра
частот. Поскольку, как было отмечено выше,
фазоинверсный фильтр ![]() является оптимальным для линейного отклика
коррелятора, то нет необходимости в
проведении оценки параметров
является оптимальным для линейного отклика
коррелятора, то нет необходимости в
проведении оценки параметров ![]() и
и ![]() для
этого фильтра. Что касается амплитудного
фильтра
для
этого фильтра. Что касается амплитудного
фильтра ![]() ,
то он заслуживает количественной оценки,
так как он более прост в практической
реализации. Такая оценка была проведена и
результаты машинных расчетов представлены
в виде графиков: зависимость
,
то он заслуживает количественной оценки,
так как он более прост в практической
реализации. Такая оценка была проведена и
результаты машинных расчетов представлены
в виде графиков: зависимость ![]() от изменения
от изменения ![]() для фильтра в виде щелей с числом N=1,2,3 и 4
на рис.4; зависимость
для фильтра в виде щелей с числом N=1,2,3 и 4
на рис.4; зависимость ![]() от изменения
от изменения ![]() для различных величин ширины щели на рис.5;
зависимость
для различных величин ширины щели на рис.5;
зависимость ![]() от изменения полосы пропускания на рис.6.
от изменения полосы пропускания на рис.6.
|
|
Рис.4.
Зависимость интенсивности
корреляционного отклика от изменения
величины e для
различного числа щелей N в
дополнительном фильтре |
|
| Рис.6.
Зависимость коэффициента e
от изменения ширины полосы пропускания
|
На рис.4 видно, что в
отклике коррелятора наблюдается
нелинейность, которая увеличивается по
мере увеличения числа щелей в
дополнительном фильтре. Это связано с тем,
что амплитудный фильтр не подавляет
существенную часть 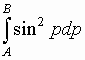 коэффициента
коэффициента ![]() .
Принимая во внимание численные результаты (рис.5
и 6), целесообразный компромисс в
отношении отклика коррелятора достигается
при использовании дополнительного
амплитудного фильтра
.
Принимая во внимание численные результаты (рис.5
и 6), целесообразный компромисс в
отношении отклика коррелятора достигается
при использовании дополнительного
амплитудного фильтра ![]() ,
содержащего 4 щели шириной
,
содержащего 4 щели шириной ![]() .
Уменьшение ширины полосы пропускания
.
Уменьшение ширины полосы пропускания ![]() приводит к уменьшению квадратичного члена
без заметного влияния на коэффициент
приводит к уменьшению квадратичного члена
без заметного влияния на коэффициент ![]() ,
но в тоже самое время ведет к снижению
уровня интенсивности
,
но в тоже самое время ведет к снижению
уровня интенсивности ![]() .
.
Характер поведения отклика
коррелятора ![]() от ширины полосы пропускания при
использовании фильтра
от ширины полосы пропускания при
использовании фильтра ![]() иллюстрируется рис.7. Видно, что
оптимизация отклика коррелятора в этом
случае состоит в максимизации допустимой
полосы пропускания
иллюстрируется рис.7. Видно, что
оптимизация отклика коррелятора в этом
случае состоит в максимизации допустимой
полосы пропускания ![]() и минимизация коэффициентов
и минимизация коэффициентов ![]() и
и ![]() .
Числовая оценка отмеченных коэффициентов
показала [9], что оптимизация
достигается при сочетании
.
Числовая оценка отмеченных коэффициентов
показала [9], что оптимизация
достигается при сочетании ![]() ,
,
![]() и
ширины полосы пропускания
и
ширины полосы пропускания ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
3.2. Преобразование информации в предметной плоскости.Рис.7. Зависимость интенсивности корреляционного отклика от изменения величины e для различных ширин полосы пропускания
= 1,5; 2,5; 3,5 для дополнительного фильтра
Повышение чувствительности голографического коррелятора за счет дополнительных фильтров, располагаемых в частотной плоскости, применимо для определенного размера деталей
- до 5 мм. Связано это с физической возможностью воздействия на пространственный спектр частот, который, как хорошо известно [10], уменьшается по мере увеличения размера деталей.Однако, проведенные нами исследования
[11] позволили установить, что повышение чувствительности коррелятора возможно и для деталей с размерами более 5 мм. Достигается это путем оконтуривания изображения в предметной плоскости коррелятора. Оконтуривание позволяет целенаправленно регулировать абсолютную погрешность голографического коррелятора. Данное обстоятельство обусловлено особенностями представления в случае контроля деталей обрабатываемой информации - в виде пропускающей свет области и однозначной связи между относительной и абсолютной погрешностями измерения.В зависимости от типа носителя информации операция оконтуривания может быть выполнена различными способами, например, путем вычитания негативного и позитивного расфокусированного изображения
, дифференцирования с помощью электронно-лучевых трубок, пропускания через соответствующие фильтры [12]. При использовании в качестве носителя информации фотопленки оконтуривание реализуется достаточно просто путем маскирования части входной плоскости системы голографической обработки информации. Так, если контролируемая деталь зарегистрирована в виде негатива, то маскирование достигается за счет размещения перед или за ним маски–шаблона, но меньших чем деталь размеров. Если же деталь зарегистрирована на фотопленке в виде позитива, то операция маскирования осуществляется путем помещения детали внутрь пропускающей свет апертуры, размеры которой больше, чем размеры контролируемой детали. При этом конфигурация маски или апертуры должна быть подобна конфигурации контролируемой детали, а их размеры выбираются из условия, что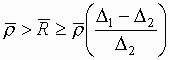 — для маски,
— для маски,
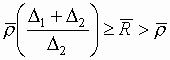 — для апертуры,
— для апертуры,
где ![]() — радиус–вектор
контролируемой детали,
— радиус–вектор
контролируемой детали,
![]() — радиус–вектор маски или
апертуры,
— радиус–вектор маски или
апертуры,
![]() и
и ![]() —
предельное и требуемое значения абсолютной
погрешности измерения.
—
предельное и требуемое значения абсолютной
погрешности измерения.
Таким образом, в результате
оконтуривания входной плоскости системы
контроля преобразуется в кольцеобразное
отверстие, границами которой служат, с
одной стороны, контур контролируемой
детали, а с другой стороны -
контур маски или апертуры. Другими словами,
информация о конфигурации детали
сохраняется, а анализируемый размер
существенно уменьшается и поэтому при
одной и той же относительной точности
контроля абсолютная точность контроля
значительно повышается. Нетрудно найти, что
абсолютная точность контроля при
использовании метода оконтуривания на
входе системы повышается в ![]() раз.
раз.
Действительно, пусть на вход системы контроля на базе голографического коррелятора поступает деталь в виде щели. Рассмотрим поведение функции взаимной корреляции без преобразования информации на входе системы контроля и в случае применения метода оконтуривания. Для упрощения будем рассматривать одномерный случай, т.е. пропускание щели в направлении оси X. Пропускание входной плоскости системы контроля без преобразования информации будет иметь вид
где
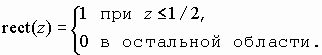
Если форма контролируемой щели совпадает с эталонной, то функция взаимной корреляции
где
При использовании метода оконтуривания пропускание входной плоскости системы контроля будет описываться выражением
где
Выражение для центрального пика, а именно, он является мерой оценки сравниваемых деталей, взаимной корреляционной функции в этом случае имеет вид
где
Поведение зависимостей
(22 и 24) дляСледует отметить, что сказанное
достигается при условии, когда оптическая
часть системы контроля имеет разрешающую
способность ![]() ,
где
,
где ![]() [13],
[13], ![]() — длина волны излучения лазера,
— длина волны излучения лазера, ![]() - числовая апертура оптической системы.
- числовая апертура оптической системы.
3.3. Разработка метода оптической фильтрации с противофазной компенсацией для допусковой разбраковки деталей
Помимо дополнительного квадратичного фильтра
Действительно, пусть после первой экспозиции (деталь
![]() ,
,
где
После второй экспозиции (деталь
![]() ,
,
где
![]() ,
,
где
Учитывая, что
Два первых члена выражения
(25), соответствующие интерференционной картине, на фильтре, оказываются, таким образом пропорциональными Фурье–спектрам разностиФизический процесс синтеза голографического двойной экспозиции с противофазной компенсацией можно пояснить рис.
9. Участок фильтра после первой экспозиции (деталь 1) изображен на рис.9, а. Интерференционная картина после второй экспозиции (деталь 2), производимой при введенииРассмотренный метод характеризуется тем, что голографический фильтр согласован не на всю деталь, а только на отличие между двумя деталями, размеры которых лежат в пределах поля допуска.
Привлекательной особенностью метода синтеза фильтра с противофазной компенсацией является то, что точность контроля размеров деталей можно изменять в широких пределах. Для этого при синтезе фильтра необходимо регистрировать определенный участок пространственных частот. Надлежащий выбор участка пространственных частот позволяет при условии перекрытия соседних дифракционных порядков во время второй экспозиции реализовать контроль партии деталей одного типа в широком диапазоне допусков с помощью всего лишь одного фильтра.
|
Часть 3 |