| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2001 |
ПУТИ РАСПРОСТРАНЕНИЯ ДЕКАМЕТРОВОЙ ВОЛНЫ В ПЛОСКОМ ОТРАЖАЮЩЕМ СЛОЕ ИОНОСФЕРЫ
В. П. Пашинцев, С. А. Тишкин, М. Э. Солчатов
Филиал Ростовского военного института ракетных войск
Получена 2 апреля 2001 г.
Разработана методика аналитического расчета фазового, реального и эквивалентного однородного путей распространения декаметровой волны в плоском отражающем слое ионосферы с параболическим распределением электронной концентрации.
Известно
[1], что форма траектории декаметровой (ДКМ) волны в процессе ее преломления и
отражения в ионосфере определяется фазовой скоростью распространения
![]() . Последняя превышает скорость света в вакууме (
. Последняя превышает скорость света в вакууме (![]() ), поскольку на любой высоте h ионосферы
коэффициент ее преломления n(h)<1.
Чтобы найти время t, затрачиваемое радиосигналом на
прохождение реального пути L=ct в
ионосфере необходимо знать групповую скорость ДКМ волны
), поскольку на любой высоте h ионосферы
коэффициент ее преломления n(h)<1.
Чтобы найти время t, затрачиваемое радиосигналом на
прохождение реального пути L=ct в
ионосфере необходимо знать групповую скорость ДКМ волны
![]() .
.
При измерении расстояний радиотехническими методами
обычно измеряют фазовое
![]() или групповое
или групповое
![]() время прихода,
определяющее протяженность фазового
время прихода,
определяющее протяженность фазового
![]() или группового
или группового
![]() пути распространения
радиоволны в ионосфере [2]. При этом для измерения L необходимо вносить поправки на фазовый
пути распространения
радиоволны в ионосфере [2]. При этом для измерения L необходимо вносить поправки на фазовый
![]() или групповой
или групповой
![]() путь.
путь.
В
[3] введено понятие эквивалентного однородного пути
![]() распространения ДКМ
волны в отражающем слое ионосферы (т.е. вдоль траектории с однородной
электронной концентрацией
распространения ДКМ
волны в отражающем слое ионосферы (т.е. вдоль траектории с однородной
электронной концентрацией
![]() , соответствующей высоте
, соответствующей высоте
![]() отражения волны), определяемого
через
отражения волны), определяемого
через
![]() .
.
В настоящее время известно [4] аналитическое выражение для расчета лишь группового пути распространения ДКМ волны, полученное в приближении плоского отражающего слоя ионосферы с параболическим распределением электронной концентрации (ЭК) по высоте N(h).
Целью статьи является разработка методики аналитического расчета фазового, реального и эквивалентного однородного путей распространения ДКМ волны в плоском отражающем слое ионосферы через групповой путь.
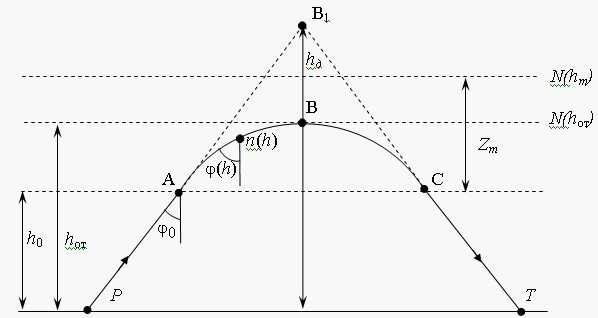
Геометрия
траектории распространения ДКМ волны с рабочей частотой
![]() , падающей под углом
, падающей под углом
![]() на нижнюю границу h=h0 плоского
отражающего слоя ионосферы, приведена на
рис.1.
на нижнюю границу h=h0 плоского
отражающего слоя ионосферы, приведена на
рис.1.
В плоскослоистой ионосфере с ростом высоты
![]()
![]() происходит постепенное увеличение ЭК N(h) в
элементарных слоях вплоть до значения
происходит постепенное увеличение ЭК N(h) в
элементарных слоях вплоть до значения
![]() , соответствующего высоте
, соответствующего высоте
![]() максимума ионизации
[1, 5, 6]. При этом величина коэффициента преломления ионосферы
уменьшается согласно выражению
максимума ионизации
[1, 5, 6]. При этом величина коэффициента преломления ионосферы
уменьшается согласно выражению
где
![]() - плазменная частота
ионосферы на высоте h.
- плазменная частота
ионосферы на высоте h.
Рис. 1. Геометрия распространения ДКМ волны
На
произвольной высоте h угол наклона траектории
![]() распространения ДКМ
волны в плоскослоистой ионосфере (рис.1) определяется из уравнения [1,
4-6]
распространения ДКМ
волны в плоскослоистой ионосфере (рис.1) определяется из уравнения [1,
4-6]
Из (1,
2) следует условие отражения ДКМ волны (в точке В на
высоте
![]() ) и соотношение для выбора ее рабочей частоты в приближении
плоской Земли и ионосферы (закон секанса):
) и соотношение для выбора ее рабочей частоты в приближении
плоской Земли и ионосферы (закон секанса):
где
![]() - частота
эквивалентной вертикально направленной волны (
- частота
эквивалентной вертикально направленной волны (![]() ), а
), а
![]() .
.
Чтобы приступить к определению фазового и реального путей ДКМ волны в ионосфере, запишем выражение для изменения фазы во фронте этой волны при ее распространении (см. рис. 1) по реальной траектории АВС [2-4]
где dl - элемент реального пути L вдоль траектории распространения ДКМ волны в ионосфере. Последний связан с элементом высоты (dh)
траектории и произвольным углом
![]() ее наклона (2)
соотношением
ее наклона (2)
соотношением
В соответствии с рис. 1 и выражением (6) протяженность реального пути ДКМ волны в ионосфере будет определяться как
Фазовый путь ДКМ волны в ионосфере определяется согласно (5-7) выражением вида
где
![]() - элемент фазового
пути.
- элемент фазового
пути.
Наиболее просто определяется групповой путь ДКМ волны в ионосфере [4]
где
![]() - элемент группового
пути.
- элемент группового
пути.
Сравнительный анализ
(7-9) указывает на выполнение
соотношений
![]() .
.
В [4] получено аналитическое выражение
для расчета
![]() при параболической
модели распределения по высоте ЭК в отражающем слое ионосферы
при параболической
модели распределения по высоте ЭК в отражающем слое ионосферы
где
![]() - полутолщина слоя.
Подстановка в (9) выражения (1) с учетом
(10) дает известное выражение
- полутолщина слоя.
Подстановка в (9) выражения (1) с учетом
(10) дает известное выражение
где
![]() - критическая частота
ионосферного слоя.
- критическая частота
ионосферного слоя.
Расчет
![]() осуществляется с
учетом следующих обстоятельств [1, 4,
5]. В законе секанса (4)
осуществляется с
учетом следующих обстоятельств [1, 4,
5]. В законе секанса (4)
![]() является функцией
истинной высоты отражения
является функцией
истинной высоты отражения
![]() , в то время как результаты ионограммы позволяют установить
взаимосвязь
, в то время как результаты ионограммы позволяют установить
взаимосвязь
![]() с действующей высотой
отражения
с действующей высотой
отражения
![]() . Поэтому для практических расчетов
. Поэтому для практических расчетов
![]() закон секанса (4)
записывают в виде
закон секанса (4)
записывают в виде
где угол
падения волны на ионосферный слой определяется на базе теорем эквивалентности
через
![]() и дальность связи R (расстояние PT на
рис. 1) из выражения
и дальность связи R (расстояние PT на
рис. 1) из выражения
Значение
![]() для параболической
модели распределения ЭК (10) рассчитывается согласно аналитическому
выражению [4, 5]
для параболической
модели распределения ЭК (10) рассчитывается согласно аналитическому
выражению [4, 5]
где параметры ионосферы
![]() ,
,
![]() и
и
![]() находят из ионограммы
(при этом полутолщину отражающего слоя
находят из ионограммы
(при этом полутолщину отражающего слоя
![]() находят по значению
находят по значению
![]() для
для
![]() , поскольку
, поскольку
![]() ).
).
Тогда в соответствии с (14) аналитическое выражение (11) для
расчета
![]() (равного пути
распространения волны по эквивалентной треугольной траектории AB1Cна
рис. 1 со
скоростью света с) можно записать в виде
(равного пути
распространения волны по эквивалентной треугольной траектории AB1Cна
рис. 1 со
скоростью света с) можно записать в виде
где
![]() определяется согласно
(13).
определяется согласно
(13).
Анализ аналитических выражений (11-15) показывает, что при приближении
![]() к
к
![]() значение
значение
![]() резко возрастает, а
увеличение
резко возрастает, а
увеличение
![]() происходит медленнее
вследствие относительно небольшого уменьшения
происходит медленнее
вследствие относительно небольшого уменьшения
![]() (13) при R=const.
(13) при R=const.
Действуя аналогичным способом, т.е. подставляя в (8) выражение (1) с учетом (10), можно получить с использованием табличного интеграла [7]
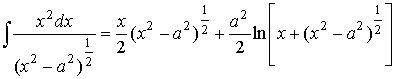
аналитическое выражение для расчета фазового пути распространения ДКМ волны в плоском отражающем слое ионосферы в виде
где
![]() - определяется
согласно (11, 15), а
- определяется
согласно (11, 15), а
![]() - согласно (13,
14).
- согласно (13,
14).
Получить удобное аналитическое выражение для расчета
реального пути
![]() аналогичным способом
прямой подстановки (1, 10) в (7) не удастся. Поэтому для решения этой задачи
воспользуемся следующей методикой [3].
аналогичным способом
прямой подстановки (1, 10) в (7) не удастся. Поэтому для решения этой задачи
воспользуемся следующей методикой [3].
Для произвольной высоты
![]() выражение (1) можно
разложить в биномиальный ряд
выражение (1) можно
разложить в биномиальный ряд
обеспечивая в расчетах два точных десятичных знака, если
второе слагаемое подкоренного выражения (т.е.
![]() /
/![]() ) не превышает 0.19 [8]. Это условие справедливости
разложения (17) для наибольших значений
) не превышает 0.19 [8]. Это условие справедливости
разложения (17) для наибольших значений
![]() можно с учетом (4)
записать в виде
можно с учетом (4)
записать в виде
При выполнении условия (18) примерное равенство (17) с учетом (1) можно записать в виде
В соответствии с (19) выражение (7) для реального пути ДКМ волны в ионосфере можно определить через фазовый (8) и групповой (9) пути как
Подстановка
в (20) выражения для
![]() (16) позволяет
получить аналитическое выражение для расчета реального пути распространения ДКМ
волны в плоском отражающем слое ионосферы в виде
(16) позволяет
получить аналитическое выражение для расчета реального пути распространения ДКМ
волны в плоском отражающем слое ионосферы в виде
Сравнительный анализ известного (11)
и полученных (16, 21) расчетных выражений указывает на выполнение соотношений
![]() .
.
Достоверность полученных выражений (16,
21) подтверждается
тем, что при выполнении условия (18) справедливости разложения (17) отличия
значений
![]() и
и
![]() от L будут иметь
одинаковую величину и противоположный знак [2]:
от L будут иметь
одинаковую величину и противоположный знак [2]:
В соответствии с (22) и расчетными выражениями (11,
16, 21)
значения поправок на групповой (![]() ) и фазовый (
) и фазовый (![]() ) путь ДКМ волны в ионосфере определяются как
) путь ДКМ волны в ионосфере определяются как
С учетом выражений для
![]() (11,
15) последнее
соотношение можно записать в более удобном для расчетов виде
(11,
15) последнее
соотношение можно записать в более удобном для расчетов виде
Анализ выражения (24) показывает, что по мере приближения
![]() к
к
![]() , т. е. роста отношения
, т. е. роста отношения
![]() , значения
, значения
![]() (14) и
(14) и
![]() (11,
15) возрастают и
пропорционально им увеличиваются поправки на групповой
(11,
15) возрастают и
пропорционально им увеличиваются поправки на групповой
![]() и фазовый
и фазовый
![]() путь. Так, при малых
отношениях
путь. Так, при малых
отношениях
![]() , когда справедливо разложение
, когда справедливо разложение
![]() при обеспечении в
расчетах двух точных десятичных знаков [8], будем иметь
при обеспечении в
расчетах двух точных десятичных знаков [8], будем иметь
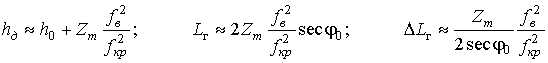 .
.
При наибольших отношениях
![]() , когда
, когда
![]() , значение
, значение
![]() .
.
В соответствии с (22) и (24) аналитические выражения для расчета реального (21) и фазового (16) путей распространения ДКМ волны в плоском отражающем слое ионосферы можно записать в более удобных видах:
где
![]() - определяется согласно
(11, 15).
- определяется согласно
(11, 15).
Теперь
определим эквивалентный однородный путь
![]() распространения ДКМ
волны в ионосфере. Заметим, что фазовый путь (8) в соответствии с (17) можно
найти как
распространения ДКМ
волны в ионосфере. Заметим, что фазовый путь (8) в соответствии с (17) можно
найти как
где поправка на фазовый
путь ![]() определяется полным количеством
электронов (ПКЭ) вдоль реального пути Lс неоднородной ЭК N(h):
определяется полным количеством
электронов (ПКЭ) вдоль реального пути Lс неоднородной ЭК N(h):
Поскольку наибольший вклад в значение
![]() будет вносить область
ионосферы с ЭК, соответствующей высоте
отражения ДКМ волны
будет вносить область
ионосферы с ЭК, соответствующей высоте
отражения ДКМ волны
![]()
![]() , значение ПКЭ (28) можно определить через L и
, значение ПКЭ (28) можно определить через L и
![]() как [3]
как [3]
где![]() - усредненное вдоль реально пути L (т.е.
однородное) значение ЭК,
- усредненное вдоль реально пути L (т.е.
однородное) значение ЭК,
![]() - эквивалентная
протяженность пути с однородной
ЭК, соответствующей высоте отражения
- эквивалентная
протяженность пути с однородной
ЭК, соответствующей высоте отражения
![]() .
.
В
соответствии с выражениями (28, 29)
![]() определяется как
определяется как
Согласно
(1, 4) отношение
![]() связанно с
коэффициентом преломления ионосферы соотношением вида
связанно с
коэффициентом преломления ионосферы соотношением вида
![]() .
.
Выражая отсюда указанное отношение через
![]() и подставляя его в
(30), получим
и подставляя его в
(30), получим
где квадрат усредненного вдоль реального пути L значения коэффициента преломления ионосферы определяется из соотношения
![]() .
.
Входящие
в (31) значения L и
![]() можно определить с
помощью общих выражений для
можно определить с
помощью общих выражений для
![]() (8) и
(8) и
![]() (7), представляемых в
виде
(7), представляемых в
виде
![]() ;
;
![]() .
.
Отсюда имеем
![]() ;
;
![]()
и выражение (31) сводится к виду
![]() .
.
Подставив сюда выражение для
![]() (26), получим
окончательное выражение для определения эквивалентного
однородного пути (
(26), получим
окончательное выражение для определения эквивалентного
однородного пути (![]() ) распространения ДКМ волны в плоском отражающем слое
ионосферы
) распространения ДКМ волны в плоском отражающем слое
ионосферы
где L и
![]() определяются согласно
(25, 24), а
определяются согласно
(25, 24), а
![]() - согласно (11,
15).
- согласно (11,
15).
Анализ
(32) показывает, что по мере роста отношения
![]() , значения Lи
, значения Lи
![]() возрастают
и
возрастают
и ![]() приближается к L. Так, при малых отношениях
приближается к L. Так, при малых отношениях
![]() , когда
, когда
![]() , будем иметь
, будем иметь
![]() ,
,
![]() ,
,
![]() .
.
При наибольших отношениях
![]() значение
значение
![]() и
и
![]() .
.
Таким образом, разработана методика, позволяющая получить аналитические выражения для расчета фазового (16, 26), реального (21, 25) и эквивалентного однородного (32) путей распространения ДКМ волны в плоском отражающем слое ионосферы с параболическим распределением электронной концентрации через известное выражение (11) или (15) для расчета группового пути.
СПИСОК ЛИТЕРАТУРЫ
1. Долуханов М.П. Распространение радиоволн. М.: Связь, 1965.
2. Колосов М.А., Арманд Н.А., Яковлев О.И. Распространение радиоволн при космической связи. М.: Связь, 1969.
3. Пашинцев. В.П., Колосов Л.В., Тишкин С.А., Антонов В.В. // РЭ. 1996. Т.41. №1. С. 21.
4. Дэвис К. Радиоволны в ионосфере. М.: Мир, 1973.
5. Калинин А.И., Черенкова Е.Л. Распространение радиоволн. М.: Связь, 1971.
6. Черенкова Е.Л., Чернышев О.В. Распространение радиоволн и работа радиолиний. М.: Радио и связь, 1984.
7. Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1969.
8. Брадис В.М. Четырехзначные математические таблицы. М.: Учпедгиз, 1962.
Авторы:
Пашинцев Владимир Петрович (shursun@mail.ru), Тишкин Сергей Алексеевич, Солчатов Максим Эриксович
Филиал Ростовского военного института ракетных войск
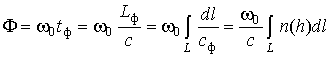 ,
(5)
,
(5)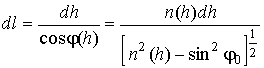 .
(6)
.
(6)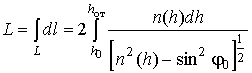 . (7)
. (7)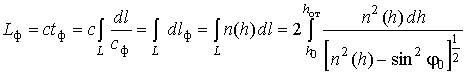 , (8)
, (8)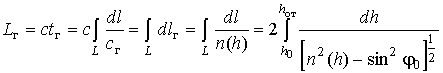 , (9)
, (9)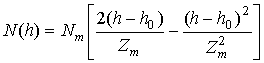 ,
(10)
,
(10)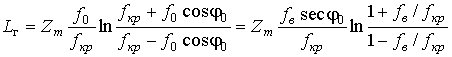 , (11)
, (11) , (14)
, (14)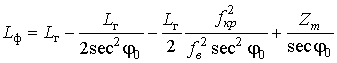 ,
(16)
,
(16)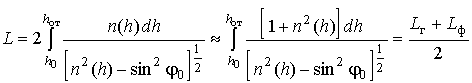 . (20)
. (20)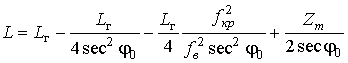 .
(21)
.
(21)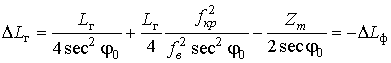 . (23)
. (23)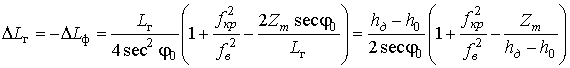 . (24)
. (24)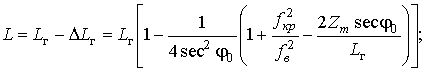 (25)
(25)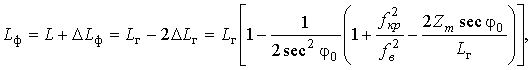 (26)
(26)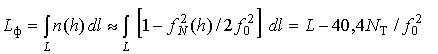 , (27)
, (27)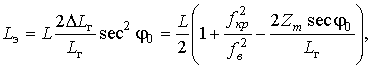 (32)
(32)