| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2001 |  |
ВЛИЯНИЕ ИМПЕДАНСНОЙ ПОВЕРХНОСТИ КРУГОВОГО ЦИЛИНДРА
НА ПОЛЕ ПРОИЗВОЛЬНО ОРИЕНТИРОВАННОГО ДИПОЛЯ
Ростовский военный институт ракетных войск
Получена 8 апреля 2001 г.
Решена задача об излучении произвольно ориентированных электрического и магнитного диполей, расположенных вблизи импедансного кругового цилиндра. Приведены соотношения, описывающие поле в произвольной точке пространства. Анализируются условия возникновения поверхностных волн. В качестве иллюстрации представлены результаты численного исследования влияния поверхностного импеданса цилиндра на распределение плотности поверхностного электрического тока и диаграмму направленности продольного электрического диполя.
Возможное применение импедансных свойств поверхности несущей конструкции для управления характеристиками излучения антенн рассматривается в большом числе работ, например, [1-9]. В материалах статьей [10-12] рассмотрены случаи возбуждения импедансных поверхностей для вариантов продольной и поперечной относительно образующей импедансного кругового цилиндра ориентации электрического диполя, расположенного вблизи него. Однако условия возникновения поверхностных волн, связанные с техникой нахождения особенностей рассеянных полей для общего случая анизотропного импеданса поверхности кругового цилиндра и произвольной ориентации электрического и магнитного диполей, не рассматривались, что позволяет говорить об актуальности темы исследований.
Целью статьи является решение задачи о нахождении поля произвольно ориентированного электрического и магнитного диполя, расположенного вблизи импедансной поверхности кругового цилиндра.
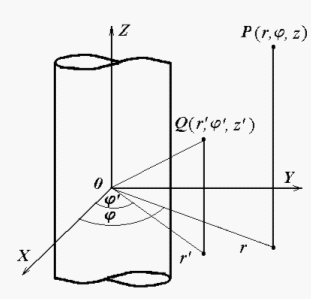
Рассмотрим однородный и
безграничный вдоль оси 0z
круговой цилиндр радиуса a с тензором поверхностного
импеданса
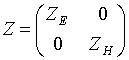 (
(![]() ‑ волновые сопротивления в классе E- и H-волн
соответственно), возбуждаемого электрическим (магнитным) диполем, произвольно
ориентированным относительно образующей цилиндра (рис. 1).
‑ волновые сопротивления в классе E- и H-волн
соответственно), возбуждаемого электрическим (магнитным) диполем, произвольно
ориентированным относительно образующей цилиндра (рис. 1).
Поскольку поле произвольно
ориентированного диполя можно представить в виде суперпозиции полей диполей,
ориентированных вдоль ортов цилиндрической системы координат, будем
рассматривать случай
![]() -ориентации диполя (
-ориентации диполя (![]() ). В этом случае ток в диполе с длиной плеча
). В этом случае ток в диполе с длиной плеча
![]() и амплитудой
и амплитудой
![]() определяется выражением
определяется выражением
где
![]() ‑ точка
расположения центра диполя.
‑ точка
расположения центра диполя.
Поскольку система однородна вдоль оси 0z, то поле расположенного вблизи кругового цилиндра диполя можно представить как в [1] в виде бесконечного спектра цилиндрических волн, распространяющихся в радиальном направлении и модулированных вдоль оси 0z
где
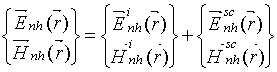 ; индексы "i",
"sc" описывают падающее и рассеянное поля
соответственно;
; индексы "i",
"sc" описывают падающее и рассеянное поля
соответственно;
![]() ‑ радиус-вектор
произвольной точки P; i‑ мнимая единица. Множитель
‑ радиус-вектор
произвольной точки P; i‑ мнимая единица. Множитель
![]() , определяющий зависимость всех величин от времени, здесь и
далее опущен.
, определяющий зависимость всех величин от времени, здесь и
далее опущен.
Продольные компоненты
падающего поля для
![]() -ориентированного электрического (индекс "e")
и магнитного (индекс "m") диполя в
соответствии с [1] описываются соотношениями
-ориентированного электрического (индекс "e")
и магнитного (индекс "m") диполя в
соответствии с [1] описываются соотношениями
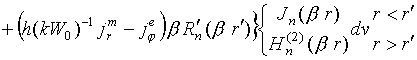 , (3)
, (3)
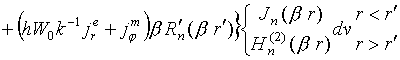 , (4)
, (4)
где
![]() Ом;
Ом;
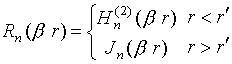 ;
;
![]() ,
,
![]() ‑ соответственно
функция Бесселя n-го порядка и ее производная и функция Ганкеля 2-го рода n-го порядка и ее производная;
‑ соответственно
функция Бесселя n-го порядка и ее производная и функция Ганкеля 2-го рода n-го порядка и ее производная;
![]() ‑ поперечное
волновое число, связанное в предположении о малых потерях в импедансной среде с
продольным волновым числом h и волновым числом
свободного пространства
‑ поперечное
волновое число, связанное в предположении о малых потерях в импедансной среде с
продольным волновым числом h и волновым числом
свободного пространства
![]() (
(![]() ‑ длина волны) соотношением
‑ длина волны) соотношением
![]() .
.
Поскольку электродинамические и геометрические параметры цилиндра не зависят от координаты z, будем считать, что рассеянное поле имеет ту же структуру, что и падающее
Коэффициенты
![]() , описывающие дифракцию волны на импедансном цилиндре в
случае отсутствия гиротропии, определяются из
граничных условий (
, описывающие дифракцию волны на импедансном цилиндре в
случае отсутствия гиротропии, определяются из
граничных условий (![]() ) [1-5]
) [1-5]
Поперечные компоненты поля являются однозначными функциями продольных компонент и могут быть найдены с использованием известных соотношений [1, 2].
С учетом приведенных выше соотношений выражения для коэффициентов дифракции принимают вид
![]() , (7)
, (7)
![]() ,
,
где
![]() ‑ символ частной
производной по r;
‑ символ частной
производной по r;
![]() ;
;
![]() ;
;
![]() ‑ угол наклона
фазового распределения соответствующей плоской волны из непрерывного спектра
волн;
‑ угол наклона
фазового распределения соответствующей плоской волны из непрерывного спектра
волн;
![]() ,
,
![]() ,
,
![]() ‑ нормированные
волновые числа, образующие уравнение нормированных поперечных коэффициентов
‑ нормированные
волновые числа, образующие уравнение нормированных поперечных коэффициентов
Несложно заметить, что
выражения, описывающие вклад деполяризационной
составляющей поля в соответствующий коэффициент дифракции, совпадают с
точностью до множителя
![]() и зависят от
поверхностного импеданса
и зависят от
поверхностного импеданса
![]() . Компонента
. Компонента
![]() тензора поверхностного
импеданса оказывает влияние только на вклад основной составляющей поля в
соответствующий коэффициент дифракции.
тензора поверхностного
импеданса оказывает влияние только на вклад основной составляющей поля в
соответствующий коэффициент дифракции.
Выполним анализ интеграла
(2) в плоскости комплексной переменной
![]() . Поскольку данная переменная является двузначной, то
комплексная плоскость является двулистной римановой поверхностью с точками
ветвления
. Поскольку данная переменная является двузначной, то
комплексная плоскость является двулистной римановой поверхностью с точками
ветвления
![]() . Для выделения однозначной ветви из точек
. Для выделения однозначной ветви из точек
![]() проведем разрезы, как
предложено в [1, 5, 8,
13] (рис.2). Из двух ветвей выберем
ту, которая соответствует затухающей волне, поскольку из физических соображений
в пассивной системе не может быть возрастающих волн [5], т.е. (
проведем разрезы, как
предложено в [1, 5, 8,
13] (рис.2). Из двух ветвей выберем
ту, которая соответствует затухающей волне, поскольку из физических соображений
в пассивной системе не может быть возрастающих волн [5], т.е. (![]() ). Анализ соотношений, полученных для рассеянного
поля, показывает, что подынтегральные функции
). Анализ соотношений, полученных для рассеянного
поля, показывает, что подынтегральные функции
![]() имеют одни и те же
полюсы при
имеют одни и те же
полюсы при
![]() , определяемые как нули знаменателя (9) в выражениях (7), (8)
для коэффициентов дифракции. Несложно заметить, что условия
возникновения поверхностных волн зависят от электродинамических свойств
поверхности кругового цилиндра, его электрических размеров и номера
пространственной гармоники.
, определяемые как нули знаменателя (9) в выражениях (7), (8)
для коэффициентов дифракции. Несложно заметить, что условия
возникновения поверхностных волн зависят от электродинамических свойств
поверхности кругового цилиндра, его электрических размеров и номера
пространственной гармоники.
Для выделения вычетов деформируем первоначальный контур интегрирования, как показано в [5]. В результате слагаемые, описывающие рассеянное поле в интегралах (2), преобразуются к виду
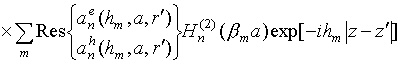 ,
,
где
![]() ‑ полуокружность
большого радиуса R в нижней полуплоскости; L ‑
петлеобразный контур, охватывающий разрез;
‑ полуокружность
большого радиуса R в нижней полуплоскости; L ‑
петлеобразный контур, охватывающий разрез;
![]() ‑ вычеты
подынтегрального выражения (5), взятые в полюсах, найденных из условия
равенства нулю соотношения (9), поскольку в рассматриваемой полуплоскости
функция Ганкеля
‑ вычеты
подынтегрального выражения (5), взятые в полюсах, найденных из условия
равенства нулю соотношения (9), поскольку в рассматриваемой полуплоскости
функция Ганкеля
![]() нулей не имеет [11].
нулей не имеет [11].
С
учетом особенности поведения подынтегральных функций при
![]() в левой части (11)
следует отбросить слагаемые, описывающие интеграл по полуокружности
в левой части (11)
следует отбросить слагаемые, описывающие интеграл по полуокружности
![]() . Интеграл по участку L
может быть вычислен путем преобразования исходного петлеобразного контура к
контуру, проходящему по реальной и мнимой полуосям комплексной переменной
. Интеграл по участку L
может быть вычислен путем преобразования исходного петлеобразного контура к
контуру, проходящему по реальной и мнимой полуосям комплексной переменной
![]() , как показано в [5].
, как показано в [5].
Совместное решение уравнений
(9) и (11) одним из предложенных в [2,
5] способов при применении подхода,
описанного в [14] и позволяющего проводить вычисления цилиндрических функций
только действительных аргументов, дает возможность найти спектр корней
дисперсионного уравнения (9). Следует отметить, что собственные числа
![]() , расположенные на мнимой полуоси (
, расположенные на мнимой полуоси (![]() ) соответствуют медленным поверхностным волнам, а
) соответствуют медленным поверхностным волнам, а
![]() , лежащие на действительной полуоси (
, лежащие на действительной полуоси (![]() ) ‑ быстрым волнам.
) ‑ быстрым волнам.
Анализ соотношения (9)
показывает, что при
![]() в системе в
зависимости от электродинамических параметров поверхности может существовать
симметричная поверхностная волна E- или H-типа,
распространяющаяся вдоль оси 0z, а при
в системе в
зависимости от электродинамических параметров поверхности может существовать
симметричная поверхностная волна E- или H-типа,
распространяющаяся вдоль оси 0z, а при
![]() ‑ гибридные
поверхностные волны. Данные вывод согласуется с положениями, приведенными в [2,
5, 13] для случаев цилиндров малого (
‑ гибридные
поверхностные волны. Данные вывод согласуется с положениями, приведенными в [2,
5, 13] для случаев цилиндров малого (![]() ) радиуса с изотропным поверхностным импедансом.
) радиуса с изотропным поверхностным импедансом.
Поверхностная волна может
распространяться и в плоскости, поперечной образующей цилиндра. Область, в
которой энергия поверхностных волн существенно преобладает над энергией
излучения, находится либо с использованием вектора Пойнтинга
как в [15] либо из определения поверхностной волны как медленной. В последнем
случае фазовый набег n-й
пространственной гармоники записывается двумя равенствами:
![]() и
и
![]() , т.е.
, т.е.
![]() . Из определения медленной волны
. Из определения медленной волны
![]() и из уравнения (10)
непосредственно следует, что
и из уравнения (10)
непосредственно следует, что
![]() , т.е.
, т.е.
Корни
дисперсионного уравнения, полученного для данной области из (9) при
использовании асимптотики
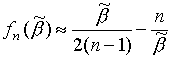 , удовлетворяющие условию (12) и лежащие на отрицательной
мнимой полуоси, описывают поверхностные волны, распространяющиеся в поперечном
относительно образующей цилиндра направлении.
, удовлетворяющие условию (12) и лежащие на отрицательной
мнимой полуоси, описывают поверхностные волны, распространяющиеся в поперечном
относительно образующей цилиндра направлении.
Для нахождения поля в
дальней зоне воспользуемся методом перевала [1, 13]. Осуществляя подстановку
![]() ,
,
![]() , а также используя асимптотику
функции Ганкеля для больших значений аргумента, несложно получить выражения
компонент векторов электрического и магнитного полей в дальней зоне. Как
показано в [5], получаемые при этом формулы справедливы в секторе углов
, а также используя асимптотику
функции Ганкеля для больших значений аргумента, несложно получить выражения
компонент векторов электрического и магнитного полей в дальней зоне. Как
показано в [5], получаемые при этом формулы справедливы в секторе углов
![]() за исключением интервала
за исключением интервала
![]() . Однако, для источников, сосредоточенных на отрезке [0,L] по
оси 0z
вблизи начала координат, при
. Однако, для источников, сосредоточенных на отрезке [0,L] по
оси 0z
вблизи начала координат, при
![]() интервал, в котором
получаемые формулы неточны, стремится к нулю.
интервал, в котором
получаемые формулы неточны, стремится к нулю.
При подстановке в соотношения (7)-(9), (11) выражений (3), (4), описывающих продольные компоненты падающего поля, несложно получить соотношения, полученные в [10-12] для случаев продольного и поперечного электрических диполей.
Приведем результаты исследования влияния импедансных свойств поверхности кругового
цилиндра на структуру поля расположенного вблизи него продольного
электрического диполя (![]() ), поскольку для данной ориентации излучателя в падающем поле
присутствует только одна компонента поля (
), поскольку для данной ориентации излучателя в падающем поле
присутствует только одна компонента поля (![]() ), что позволяет легко анализировать получаемые результаты.
), что позволяет легко анализировать получаемые результаты.
Коэффициенты дифракции для данного диполя описываются формулами
где
![]() ;
;
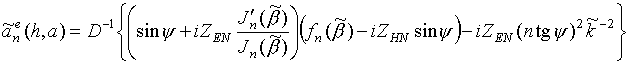 .
.
Компоненты плотности поверхностного электрического тока (поле в ближней зоне), как показано в [10], и векторной ДН (поле в дальней зоне) определяются соотношениями:
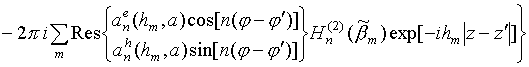 ,
,
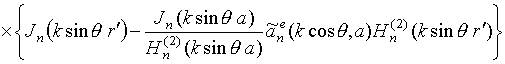 ;
;
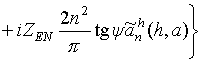 ;
(18)
;
(18)
![]() ; * ‑ символ комплексного сопряжения.
; * ‑ символ комплексного сопряжения.
Выражения (16), (17)
совпадают с формулами, приведенными в [1, 16,
17] для частного случая
![]() , а также для полученных другим
методом.
, а также для полученных другим
методом.
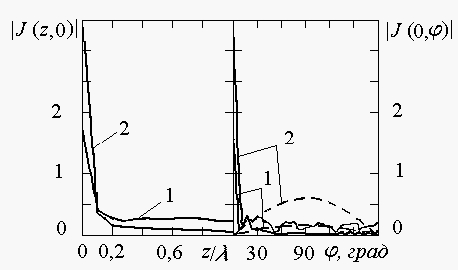
Результаты исследований
влияния параметров поверхностного импеданса на распределение плотности поверхностного
электрического тока и компоненты ДН продольного электрического диполя,
расположенного на удалении
![]() от поверхности
кругового цилиндра радиуса
от поверхности
кругового цилиндра радиуса
![]() , показаны на рис.
3, 4. Кривые 1 и 2 на обоих рисунках иллюстрируют
результаты, полученные для изотропного (
, показаны на рис.
3, 4. Кривые 1 и 2 на обоих рисунках иллюстрируют
результаты, полученные для изотропного (![]() ) и анизотропного (
) и анизотропного (![]() ,
,
![]() ) поверхностного импеданса соответственно. Сплошной линией
иллюстрируется поведение основной компоненты (z-компоненты
для поверхностного тока и
) поверхностного импеданса соответственно. Сплошной линией
иллюстрируется поведение основной компоненты (z-компоненты
для поверхностного тока и
![]() -компоненты для ДН), а штриховой линией ‑ деполяризационной (
-компоненты для ДН), а штриховой линией ‑ деполяризационной (
![]() -компонента в обеих зонах). Левое поле
рис. 3 описывает сечения
амплитудного распределения компонент плотности поверхностного тока плоскостью
-компонента в обеих зонах). Левое поле
рис. 3 описывает сечения
амплитудного распределения компонент плотности поверхностного тока плоскостью
![]() , правое ‑ плоскостью
, правое ‑ плоскостью
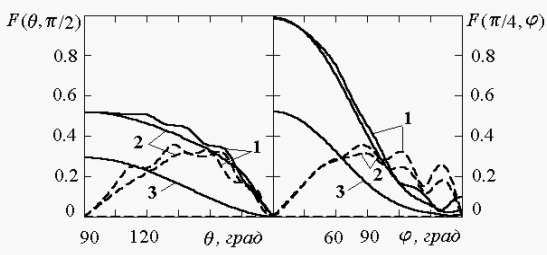
![]() . На рис.4 кривые 3 соответствуют данным, полученным для
случая идеально проводящей поверхности цилиндра. Левое поле отражает сечения
компонент объемной ДН плоскостью
. На рис.4 кривые 3 соответствуют данным, полученным для
случая идеально проводящей поверхности цилиндра. Левое поле отражает сечения
компонент объемной ДН плоскостью
![]() , правое поле ‑ плоскостью
, правое поле ‑ плоскостью
![]() .
.
Анализ приведенных
результатов показывает, что размещение диполя вблизи импедансной поверхности
кругового цилиндра вызывает эффективное взаимодействие поля диполя с
импедансной поверхностью, заключающееся в изменении структуры рассеянного поля
(появлении деполяризационной компоненты,
отсутствующей в падающем поле), а также в возбуждении поверхностных волн,
амплитуда и направление распространения которых зависит от электродинамических
свойств поверхности цилиндра. Изменение структуры рассеянного
поля приводит к перераспределению энергии, излучаемой системой в различных
направлениях, поскольку основная и деполяризационная
составляющие имеют различную угловую зависимость, что отражается в пространственной
ориентации максимумов компонент поля. Так, основная составляющая поля
достигает максимальных значений в секторе углов
![]() в плоскости
в плоскости
![]() . Деполяризационная составляющая в
данной плоскости обращается в нуль, ее максимум наблюдаются в секторе углов
. Деполяризационная составляющая в
данной плоскости обращается в нуль, ее максимум наблюдаются в секторе углов
![]() .
.
Замедление волны, как
несложно заметить из рис.3,
растет по мере удаления от точки соприкосновения фазового фронта падающей волны
с поверхностью цилиндра. Направление распространения поверхностной волны
зависит от типа импеданса. Так, в случае изотропного импеданса в спектре
поверхностных волн преобладают волны, распространяющиеся вдоль образующей
цилиндра и включающие помимо гибридных волн симметричную волну. Амплитуда z-компоненты
плотности поверхностного тока для данного импеданса имеет максимум в точке,
расположенной непосредственно под диполем, а при
![]() является практически
постоянной, хотя в поперечной плоскости наблюдается быстрое затухание волны.
Для анизотропного импеданса наблюдается возникновение поверхностной волны,
распространяющейся в поперечном направлении. Однако, поскольку возбуждаемая
волна соответствует большим значениям гармоник, то эффект поверхностной волны
проявляется в виде осцилляций распределения амплитуды поверхностного тока. В
направлении образующей цилиндра наблюдается при этом изменение амплитуды по
закону, близкому к экспоненциальному.
является практически
постоянной, хотя в поперечной плоскости наблюдается быстрое затухание волны.
Для анизотропного импеданса наблюдается возникновение поверхностной волны,
распространяющейся в поперечном направлении. Однако, поскольку возбуждаемая
волна соответствует большим значениям гармоник, то эффект поверхностной волны
проявляется в виде осцилляций распределения амплитуды поверхностного тока. В
направлении образующей цилиндра наблюдается при этом изменение амплитуды по
закону, близкому к экспоненциальному.
Таким образом, наличие кругового цилиндра с импедансными свойствами поверхности приводит к изменению структуры поля диполя как в ближней, так и в дальней зонах, что выражается в появлении деполяризационной составляющей, отсутствующей в случае идеально проводящей поверхности цилиндра, а также в появлении поверхностных волн, амплитуда и направление распространения которых зависит как от ориентации диполя, так и от электродинамических свойств поверхности. Условия возбуждения поверхностных волн (полюсы) для электрических и магнитных диполей одинаковы.
Рис.3 Распределение плотности поверхностного электрического тока
на круговом цилиндре радиуса ![]() продольным
электрическим диполем,
продольным
электрическим диполем,
удаленным от
поверхности цилиндра на ![]() ,
,
для различных значений поверхностного импеданса
(1 - ![]() ; 2 -
; 2 - ![]() ,
, ![]() ;
;
сплошная линия - z-компонента; штриховая линия - ![]() -компонента)
-компонента)
Рис.4. Сечения компонент объемной ДН, возбуждаемой продольным
электрическим
диполем, удаленным от поверхности цилиндра радиуса ![]()
на ![]() , для различных значений поверхностного импеданса
, для различных значений поверхностного импеданса
(1 - ![]() ; 2 -
; 2 - ![]() ,
, ![]() ; 3 -
; 3 - ![]() ;
;
сплошная линия - ![]() -компонента;
штриховая линия -
-компонента;
штриховая линия - ![]() -компонента)
-компонента)
Литература
1. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. ‑ М.: Радио и связь, 1983. 296 с.
2. Вайнштейн Л.А. Электромагнитные волны. ‑ М.: Радио и связь, 1988. ‑ 440 с.
3. Уэйт Д.Р. Электромагнитное излучение из цилиндрических систем. ‑ М.: Сов. радио, 1962. ‑ 239 с.
4. Пресс А.А. Влияние проводимости эллиптического цилиндра на структуру поля электрического вибратора, параллельного его оси // Тр. Гос. НИИрадио, 1988, №3, С.47-51.
5. Шевченко В.В. Плавные переходы в открытых волноводах ‑ М.: Наука, 1969. ‑ 192 с.
6. Tenneti R. Plane wave scattering by a corrugated conducting cylinder at oblique incidence // IEEE Trans. AP-36. 1988. №8. С.1184-1188.
7. Апельцин В.Ф. Высокочастотное возбуждение Е-поляризованным полем точечного источника тонкого диэлектрического покрытия гладкого металлического цилиндра // Электромагнитные волны & Электронные системы. 2000. Т.5. №1. С.4-17.
8. Кюркчан А.Г. Возбуждение нитью тока периодической ребристой структуры, обладающей свойствами искусственно жесткой поверхности // Радиотехника и электроника. 1999. Т.44. №7. С.787-793.
9. Звягинцев А.А., Батраков Д.О. Дифракция на эллиптическом импедансном цилиндре // Изв. вуз. Радиофизика. 1989. №9. С.1125-1131.
10. Каценеленбаум Б.З. Высокочастотная электродинамика. ‑ М.: Наука, 1966.
11. Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Возбуждение импедансной поверхности цилиндра продольным электрическим диполем // "Журнал радиоэлектроники". 2000. №6. http://jre.cplire.ru/win/jun00/6/text.html
12. Звездина М.Ю. Поле поперечного электрического диполя, расположенного вблизи импедансного кругового цилиндра // "Журнал радиоэлектроники". 2000. №9. http://jre.cplire.ru/win/sep00/2/text.html
13. Габриэльян Д.Д., Звездина М.Ю., Звездина Ю.А. и др. Возбуждение импедансной поверхности цилиндра поперечным электрическим диполем // "Журнал радиоэлектроники". 2000. №10. http://jre.cplire.ru/win/oct00/6/text.html
14. Кравцов В.А. Поле радиального электрического вибратора, расположенного вблизи идеально проводящего кругового цилиндра // Радиотехника. 1973. Т.28. №8. С.43-50.
15. Ерохин Г.А., Кочержевский В.Г., Гофман В.Г. Синтез цилиндрических антенных решеток // "Антенны". Вып. 17. ‑ М.: Связь, 1973. С.43-52.
16. Габриэльян Д.Д., Звездина М.Ю. Излучение линейной антенны, ориентированной продольно импедансному круговому цилиндру // Акустический журнал. 1997. Т.43. №4. С.548-550.
17. Габриэльян Д.Д., Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на диаграмму направленности электрического диполя // Радиотехника и электроника. 2000. Т.45. №10. С.1194-1197.
Автор: Звездина Марина Юрьевна ‑ кандидат технических наук, РВИ РВ, zvezd@jeo.ru
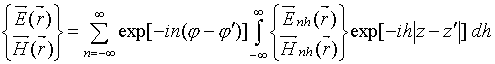 , (2)
, (2)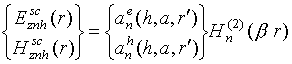 .
(5)
.
(5)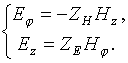
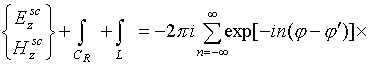 (11)
(11)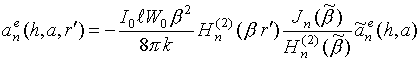 ,
(13)
,
(13)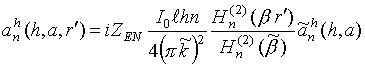 ,
(14)
,
(14)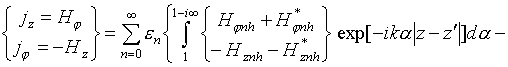 (15)
(15)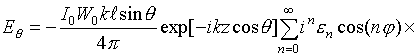
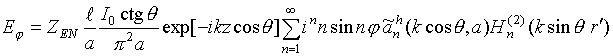 ; (17)
; (17)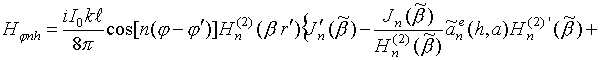
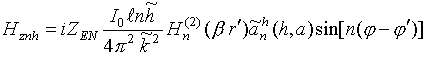 ;
(19)
;
(19)