| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5 , 2000 |
О МНОГОКРАТНЫХ ОТРАЖЕНИЯХ В НЕОДНОРОДНОЙ ЛИНИИ ПЕРЕДАЧИ
В.В. Меркулов, И.С.
Синева
Московский технический университет
связи и информатики
Получена 26 марта 2000 г.
Получена после доработки 12 мая 2000 г.
Рассматривается задача рассеяния в одномодовой линии передачи с конечным числом неоднородностей. Получены явные решения для прошедшей и отраженной волн. Для однородных рассеивателей показана связь найденных явных решений с многочленами Белла.
Рассмотрим одномодовую однородную линию передачи, в которую включено
s+1 неоднородностей (рассеивателей). Каждая n-ая неоднородность характеризуется комплексным параметромРис. 1. Преобразование напряжения при прохождении единичной волны через рассеиватель с номером
nРис. 2. Преобразование тока при прохождении единичной волны через рассеиватель с номером
nПусть на вход первой неоднородности падает единичная волна. Она испытывает многократные отражения. В результате на выходе линии будем иметь сигнал
T(s+1) , а на входе – отраженный сигнал R(s+1) . Для соответствующих напряжения и тока введем обозначения:В простейшем случае
(s=1)(1)
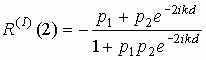 ,
,
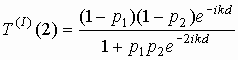 .
.
Здесь
d – длина линии, соединяющей первую и вторую неоднородности, а k – волновое число для этой линии. Обобщение формул (1) на случай s>1 приводит к рекуррентным соотношениям:(2)
 ,
,
Здесь
Рекуррентные соотношения (2) представляют самостоятельный интерес и могут быть использованы при численном моделировании описанной линии. Вместе с тем, для качественного анализа необходимо иметь непосредственное выражение для
Пусть на неоднородность с номером
n слева падает волна с единичными амплитудой и напряжением. Обозначим черезДля введенных величин ![]() ,
,
![]() ,
, ![]() ,
,![]() можно написать рекуррентные соотношения из
следующих соображений: единичная волна,
упавшая слева на n-ый рассеиватель,
разделяется на две: одна волна слева падает
на (n+1)-ый рассеиватель, другая падает
справа на (n-1)-ый рассеиватель. Обе эти
волны дают свой вклад в
можно написать рекуррентные соотношения из
следующих соображений: единичная волна,
упавшая слева на n-ый рассеиватель,
разделяется на две: одна волна слева падает
на (n+1)-ый рассеиватель, другая падает
справа на (n-1)-ый рассеиватель. Обе эти
волны дают свой вклад в ![]() (
(![]() ).
).
При ![]()
Аналогично, единичная волна, упавшая справа на n-ый рассеиватель, разделяется на волну, падающую справа на (n-1)-ый рассеиватель, и волну, падающую слева на (n+1)-ый рассеиватель. Таким образом, при тех же значениях n
Граничные условия к уравнениям (3) , (4) имеют вид:
В терминах переменных ![]() и
и ![]() нас
интересуют величины
нас
интересуют величины ![]() ,
,
![]() .
.
Теорема. Решение уравнений (3),
(4) с граничными условиями (5)
относительно ![]() ,
,
![]() имеет
вид:
имеет
вид:
где при ![]()
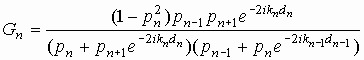 .
.
Решение для ![]() получается для
получается для ![]() при значениях параметров
при значениях параметров

![]() ,
а решение для
,
а решение для ![]() - при значениях
- при значениях
 и
и
![]() .
.
Доказательство теоремы
проведем, например, дляИсключим из (7)
переменные ![]()
Переходя в (8) от индекса
n-1 к индексу n, получаем (9)Подставив соотношения (8) и (9) в (7), имеем
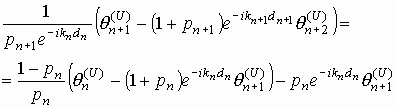
или
![]() .
.
Введя величины
![]() ,
,
![]() ,
,
получим уравнение в виде
На решении уравнений (10) с граничным условием
Для доказательства соотношения (11) воспользуемся индукцией по переменной
s. Пусть (11) верно при всехИз (11) следует, что
 ,
,
 .
.
Тогда
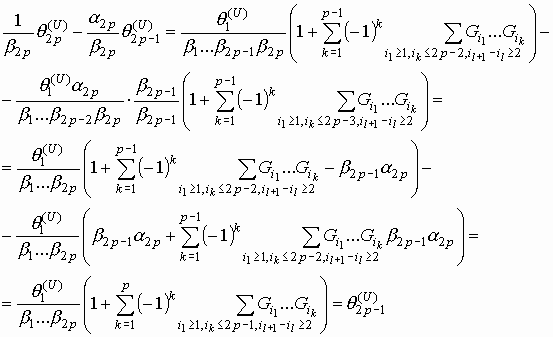
Мы
воспользовались тем, что ![]() .
Таким образом, (12) доказано, а
значит и (11) установлено для всех
четных s.
Доказательство для нечетных s
проводится аналогично.
.
Таким образом, (12) доказано, а
значит и (11) установлено для всех
четных s.
Доказательство для нечетных s
проводится аналогично.
Результат
теоремы получается их (11) и того,
что ![]() .
.
В качестве
частного случая рассмотрим решение (6)
при ![]() ,
,
![]() .
Тогда
.
Тогда ![]() ,
,
![]() при
при ![]() и
и
где ![]() - число таких разбиений s-множества
- число таких разбиений s-множества
![]() ,
, ![]() ,
что
,
что
Из (14)
следует, что ![]() .
Тогда
.
Тогда ![]() ,
где
,
где ![]() - полином Белла (см., например, [1]).
Используя установленное тождество, запишем
(13) в виде
- полином Белла (см., например, [1]).
Используя установленное тождество, запишем
(13) в виде
Из (15), в частности, следует, что в первом приближении
Поскольку
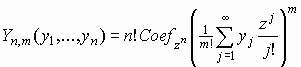
(см.
[1] ), то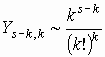 при больших значениях k,
т.е. соответствующие слагаемые в (15)
очень быстро убывают и экспоненциальное
затухание имеет место не только в первом
приближении.
при больших значениях k,
т.е. соответствующие слагаемые в (15)
очень быстро убывают и экспоненциальное
затухание имеет место не только в первом
приближении.
Рекуррентные соотношения (2) замечательны тем, что учитывают бесконечное число отражений в линии с
s+1 неоднородностями. В этом смысле выражения (2) являются строгими. В тоже время во многих типичных ситуациях необходимо иметь представление об асимптотическом поведении характеристик при увеличении количества параметров (т.е. при росте s). В этом смысле недостатком соотношений (2) является отсутствие «наглядности» предельного поведения характеристик, что в ряде задач заставляет переходить к приближенным выражениям. Например, при изучении волноводов со случайными неоднородностями ограничиваются условиямиЛитература
Авторы:
Меркулов Всеволод Владимирович, д.т.н.,
профессор
Синева Ирина Сергеевна, к.ф.-м.н., доцент, e-mail:
irina.sineva@mtu-net.ru