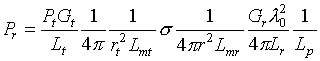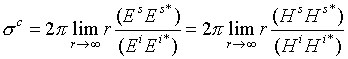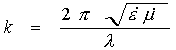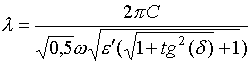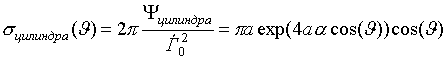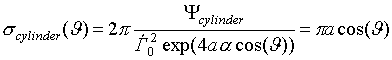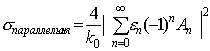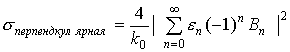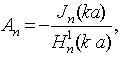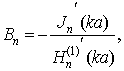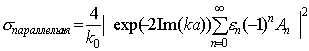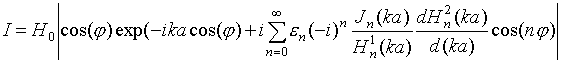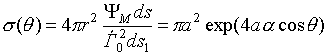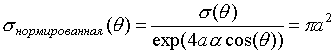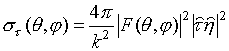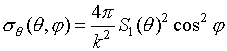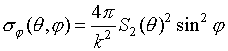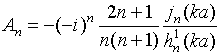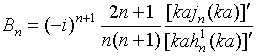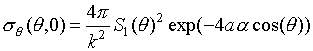Эффективная площадь рассеяния идеально проводящих тел простейшей формы в средах с комплексной проницаемостью

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2001

оглавление

дискуссия

ЭФФЕКТИВНАЯ ПЛОЩАДЬ РАССЕЯНИЯ ИДЕАЛЬНО ПРОВОДЯЩИХ ТЕЛ ПРОСТЕЙШЕЙ ФОРМЫ В СРЕДАХ С КОМПЛЕКСНОЙ ПРОНИЦАЕМОСТЬЮ

Р. М. Седлецкий

Московский государственный авиационный университет

Получена 2 октября 2001 г.

Эффективная площадь рассеяния (ЭПР) является результатом нормировки мощности отражённого поля к мощности падающей плоской волны. Показывается, что для расчета ЭПР в средах с потерями необходима коррекция нормировки, принятой для свободного пространства. Для сред с потерями необходимо нормировать мощность отражённого поля к мощности падающей волны, отнесённой к фронтальной части тела. Коррекция должна быть сделана для всех углов двухпозиционности, кроме угла, равного (локация на просвет). Показывается, что ЭПР существенно зависит как от действительной, так и от мнимой части диэлектрической проницаемости среды, окружающей рассеивающий объект.

Ключевые слова: ЭПР, комплексная диэлектрическая проницаемость, рассеяние, идеально проводящий цилиндр, идеально проводящая сфера, двухпозиционная локация.

Введение

ЭПР характеризует отражающие свойства цели, позволяя оценивать дальность обнаружения радиолокатора. Согласно [1,2], мощность отражённого сигнала на входе приёмной антенны имеет вид

(1)

Где:

- мощность передатчика в Вт,

- коэффициент усиления передающей антенны в направлении цели,

- коэффициент, учитывающий потери в передающей системе,

- коэффициент, учитывающий потери в приёмной системе,

- расстояние между передающей антенной и целью,

- ЭПР цели,

- коэффициенты, учитывающие потери в среде распространения между пере-

дающей антенной и целью, а также между целью и приёмной антенной.

- дальность между целью и приёмной антенной,

- коэффициент усиления приемной антенны в направлении цели,

- длина волны в среде распространения,

- коэффициент, учитывающий поляризационные потери.

Из формулы (1) получаем выражения для ЭПР цели

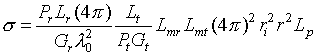
Предполагая, что потери в среде распространения отсутствуют, имеем классическое выражение для ЭПР [1,2]

(2)

где и электрическая и магнитная составляющие отраженного поля, соответственно, и – составляющие падающего поля. Для бесконечных и полубесконечных тел вводится определение ЭПР в виде

(3)

При ЭПР в выражениях (2,3) не зависит от дальности и характеризует отражающие свойства объекта. Для приведенных выше традиционных выражений ЭПР (2,3) следует отметить два существенных обстоятельства:

A. ЭПР вводится как характеристика, не зависящая от свойств среды распространения. Может быть поэтому в литературе укоренилась точка зрения, что ЭПР не зависит от свойств среды распространения [1].

B. В среде распространения без потерь амплитуда плоской волны и нормировка в выражениях (2,3) не вызывает проблем. В среде с потерями амплитуда плоской волны экспоненциально убывает вдоль рассеивающего объекта и от выбора нормирующей амплитуды в (2,3) будет зависеть величина ЭПР.

В справочнике [2] ЭПР рассчитаны для сред без потерь. Для расчета ЭПР в средах с потерями в [2] предлагается перейти к комплексной диэлектрической проницаемости и рассчитывать ЭПР согласно выражениям (2,3). Выбор нормирующей амплитуды в [2] не обсуждается. Как показывается ниже, такой способ расчета ЭПР приемлем только в случаях, когда можно пренебречь изменением амплитуды падающей плоской волны вдоль отражающего объекта.

В подповерхностной радиолокации [4], в задачах медицинской диагностики [5 - 7] необходимо учитывать затухание плоской падающей волны вдоль отражающего объекта.. В этих случаях, при расчете ЭПР, помимо перехода к комплексным волновым числам, необходим также корректный выбор нормирующей амплитуды падающей плоской волны в выражениях (2,3).

1. Распространение плоской волны в среде с потерями

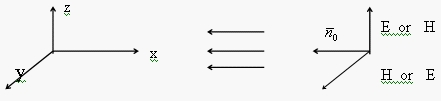
Предположим, что плоская волна распространяется вдоль оси x, со стороны . Направление распространения – параллельно оси x , как это показано на рис.1.

Рис. 1. Распространение плоской волны в среде распространения с потерями.

В этом случае выражение для плоской волны может быть записано в виде:

(4)

где: - угловая частота, - волновое число среды распространения, - амплитуда плоской волны. Параметры среды распространения входят в выражение для волнового числа следующим образом [3]:

(5)

здесь: и - комплексная магнитная и диэлектрическая проницаемости среды распространения. Далее полагается, что = 1.

или (6)

и - действительная и мнимая части диэлектрической проницаемости, -тангенс угла потерь, - длина волны в свободном пространстве . Длина волны зависит как от , так и от . Если то выражение для длины волны запишется в виде [4]:

(7)

здесь - скорость света в свободном пространстве. Из выражения (7) видно, что длина волны в среде с комплексной проницаемостью зависит как от действительной части диэлектрической проницаемости, так и от величины потерь в среде распространения. Постоянная распространения связана с комплексным волновым числом как

, (8)

здесь: - коэффициент поглощения, - фазовая постоянная. Выбор знака в выражениях (8,9) зависит от направления распространения волны. Если волна распространяется со стороны , как это показано на рис. 1, знак в (8,9) должен быть положительным. Подставляя (8) в (4), имеем

(9)

соответственно:

или . (10)

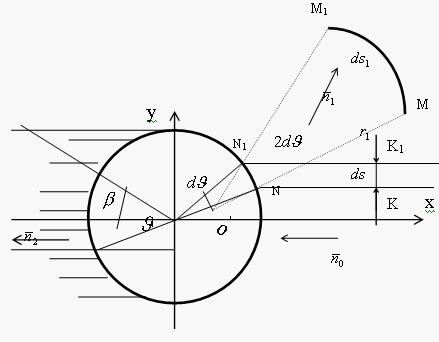
2 Отражение плоской волны от бесконечного идеально проводящего цилиндра в среде с потерями

2 -1. Метод геометрической оптики (ka >> 1).

С точки зрения геометрической оптики ЭПР цилиндра не зависит от направления поляризации падающей плоской волны. Предположим, что плоская волны падает перпендикулярна оси цилиндра (ось z ) со стороны , как это показано на рис. 2 [8]. Плоскости y = a и y = - a являются границами света и тени.

Рис. 2. Геометрия отражения от бесконечного, кругового цилиндра.

На поверхности цилиндра в точке N с координатамиинтенсивность плоской волны запишется в виде:

(11)

Здесь - амплитуда падающей волны, – коэффициент затухания. Заметим, что только в плоскости амплитуда падающей волны равна , независимо от величины потерь в среде распространения. Согласно принципу зеркального отражения в точке Nугол отражения равен, соответственно, в точке - . Расстояние вдоль оси y между точками и , равно . Расстояние между точками и равно , здесь - расстояние между точкой N на поверхности цилиндра с координатами и точкой наблюдения с координатами . Для достаточно больших , , и интенсивность падающей волны, проходящей через единичную площадку вдоль оси z имеет вид

Интенсивность отраженной волны в точке наблюдения , для равно

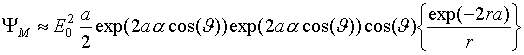Если воспользоваться нормировкой [2], получим выражение для ЭПР цилиндра

. (12)

Для обратного рассеяния () отражающая ширина принимает вид

. (13)

Заметим, что ЭПР цилиндра (12, 13) экспоненциально возрастает с увеличением произведения радиуса на коэффициент поглощения . Полученный результат связан с некорректным выбором амплитуды падающий плоской волны в нормировке (2, 12). В выражении (12) интенсивность плоской волны соответствует сечению , - "центру цилиндра". Если нормировать к интенсивности плоской волны, соответствующей блестящей точке, получаем известный результат:

(14)

Важно отметить, что геометрическая теория дифракции показывает необходимость изменения нормировки [2] для сред с потерями.

2 - 2. Отражение плоской волны от бесконечного идеально проводящего цилиндра в среде с потерями. Точное решение.

ЭПР цилиндра при обратном рассеянии записывается в виде [2]

и (15)

где коэффициенты и выражаются через цилиндрические функции Бесселя, Ханкеля и их производные [9]

. (16)

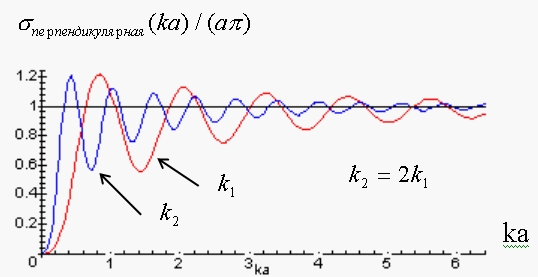
Рассмотрим влияние действительной и мнимой части диэлектрической проницаемости на ЭПР цилиндра. Вначале предположим, что диэлектрическая проницаемость - действительная величина (среда без потерь). Направление поляризации - перпендикулярно оси цилиндра. На рис. 3 представлена зависимость нормированной ЭПР для двух волновых чисел, одно из которых в два раза больше, чем другое . Увеличение диэлектрической проницаемости уменьшает длину волны, согласно выражению (7), и в результате этого имеет место увеличение ЭПР при малых значениях волновых чисел.

Рис. 3. Зависимость нормированной ЭПР цилиндра для двух значений волновых чисел , соответственно .

Полученный результат хорошо известен. В релеевской области рассеяния ЭПР возрастает обратно пропорционально четвертой степени длины волны, или согласно (7) пропорционально [2,3].

Результат вычисления ЭПР для комплексных аргументов представлены на рис. 4. Направление поляризации перпендикулярно оси цилиндра. Кривая 1 вычислена согласно выражениям (16 - 17) [2]. Кривая 2 - результат вычисления методом геометрической оптики (выражение 13).

Рис. 4. Зависимость нормированной ЭПР от параметра , Вектор Е перпендикулярен оси цилиндра. Кривая 1 получена на основе рядов Ми, кривая 2 рассчитана методом геометрической оптики, в обоих случаях .

Как видно из рис. 4, ЭПР возрастает экспоненциально с увеличением параметра . Как это было отмечено ранее, полученный результат связан с некорректной нормировкой [2]. Если нормировать, согласно (14), то ЭПР цилиндра следует записать в виде:

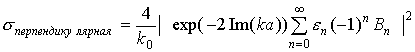(17)

где коэффициенты и определяются согласно (16), .

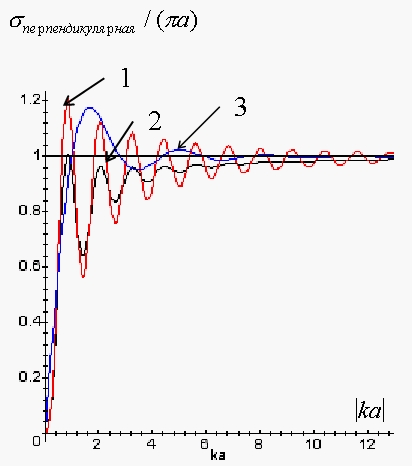
Результаты вычисления ЭПР, согласно выражениям (16, 17) представлены на рис. 5. Кривая 1 соответствует среде без потерь, кривые 2 и 3 соответствуют среде с потерями k = 1+ 0.07i. Кривая 3 на рис. 5 рассчитана методом физической оптики [8]. С учетом нормировки (17), для сред с потерями, при и , ЭПР цилиндра запишется в виде:

₍₁₈₎

Рис. 5. ЭПР бесконечного идеально проводящего цилиндра. Направление поляризации перпендикулярно оси цилиндра. Кривая 1 соответствует среде без потерь, кривые 2 и 3 - среде с потерями k = 1+ 0.07i. Кривые 1 и 2 – точное решение, кривая 3 – приближение, даваемое физической оптикой. Кривая (1) рассчитана согласно выражению (15), кривая (2) – согласно выражению (17), кривая (3) – согласно выражению (18).

Из рис.5 можно видеть, что для среды с потерями уровень осцилляции ЭПР гораздо меньше, чем это имеет место в среде без потерь. Осцилляции ЭПР обусловлены сложением двух волн, одна из которых отражается от лобовой части цилиндра, вторая огибает цилиндр и также дает свой вклад в ЭПР. В среде с потерями вклад, вносимый ползущей волной уменьшается с ростом произведения , соответственно, уменьшается и уровень осцилляций ЭПР.

Согласно (15,17) была рассчитана ЭПР цилиндра для поляризации, параллельной оси цилиндра Практически, ЭПР для среды с потерями и среды без потерь не отличаются.

2 - 3. Влияние потерь окружающей среды на величину поверхностных токов, текущих по поверхности идеально проводящего цилиндра. Поляризация параллельна оси цилиндра.

Для среды без потерь, распределение тока по поверхности цилиндра было рассчитано Потехиным [8]

(19)

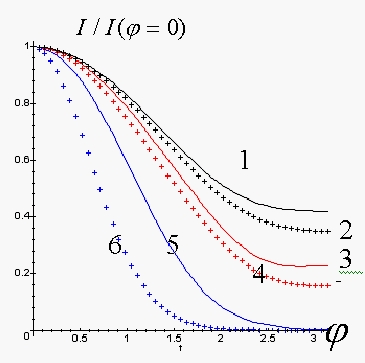
Зависимость нормированной амплитуды тока от параметра представлена на рис. 6. Сплошные кривые соответствуют среде без потерь, пунктирные кривые - среде с потерями. Как видно из рис. 6, с увеличением для среды без потерь амплитуда тока уменьшается на теневой стороне цилиндра и в пределе при , ток течет только по освещенной стороне цилиндра (приближение Кирхгофа).

Рис. 6. Распределение амплитуды тока по поверхности цилиндра. Направление поляризации - перпендикулярно оси цилиндра.

1 - , 2 - , 3 - , 4- , 5 - , 6 - .

Наличие потерь в среде, окружающей цилиндр, меняет распределение тока по поверхности цилиндра. С увеличением параметра уменьшается амплитуда плоской волны, падающая на поверхность цилиндра, кривые 4 - 6 на рис. 6, что в конечном счете приводит к уменьшению амплитуды поверхностного тока на освещенной части цилиндра (кривая 6 на рис. 6).

3. ЭПР идеально проводящей сферы в среде с потерями

3-1. Геометрическая оптика

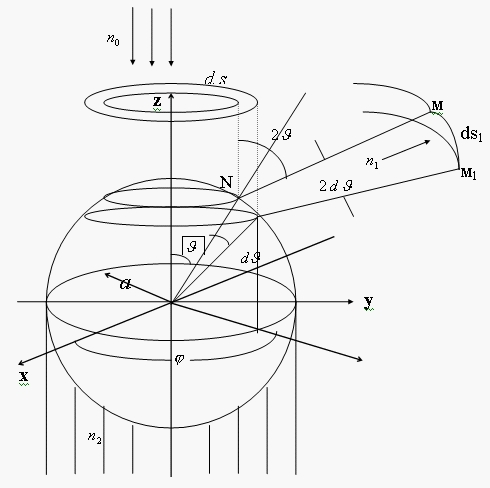
Геометрия отражения представлена на рис. 7. Плоская волна движется в z направлении (со стороны z > 0). Выделим на поверхности сферы круговую полоску радиусом и шириной [8]. Эта полоска освещается плоской волной, проходящей через кольцо, находящимся в плоскости , с площадью

Мощность волны, падающей на поверхность сферы в среде с потерями определяется как

(20)

Отраженная волна распространяется в области, заключенной между двумя конусами с углы которых равны и . При , отраженная волна освещает полоску с площадью, равной

Расстояние между точкой на поверхности сферы и точкой наблюдения при равняется . Интенсивность отраженной волны в точке запишется в виде

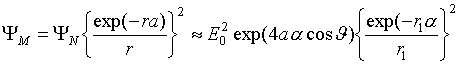, при

Рис. 7. Геометрия отражения от сферы

Делая подстановку , и используя нормировку [2] получаем

(21)

Из формулы (21) следует, что ЭПР сферы экспоненциально возрастает с увеличением произведения . Причина экспоненциального роста ЭПР сферы связана с некорректным выбором нормирующей амплитуды в (2). Если положить, что амплитуда падающей волны равна в блестящей точке на поверхности сферы, получаем хорошо известный результат

(22)

3 - 2. Двухпозиционная ЭПР идеально проводящей сферы в средах с потерями, ряды Ми [2].

Геометрия отражения показана на рис. 7, пусть плоская волна движется в z направлении (со стороны z > 0). Вектор E параллелен оси x,

, .

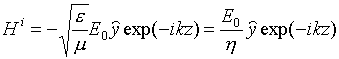- единичные орты. Точка приема имеет сферические координаты . Электрическая напряженность в дальней зоне ( ) имеет вид

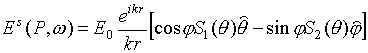
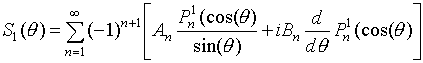где и комплексные амплитуды отраженного поля в дальней зоне для и направлений поляризации

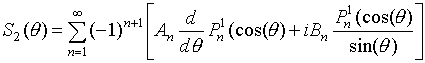Здесь: - присоединенные функции Лежандра первого рода [9]. Вектор отраженного поля запишется в виде

Согласно [2], двухпозиционная ЭПР в произвольном направлении поляризации , для случая, когда вектор поляризации падающей волны поляризован в x направлении имеет вид

(23)

Парциальные составляющие ЭПР дляи поляризации получаются из (13), если подставить и

, (24)

Рис. 8. Эффективная площадь обратного рассеяния идеально проводящей сферы в среде с потерями.

1 - среда без потерь, 2 - ka = a(1+0.05i), 3 - ka = a(1+0.1i).

Для идеально проводящей сферы коэффициенты А_nи В_nимеют вид

, (25)

гдеand - сферические функции Бесселя и Ханкеля [9]. - производная по аргументу . С использованием нормировки (22), ЭПР обратного рассеяния запишется в виде

(26)

Эффективная площадь обратного рассеяния, вычисленная по формулам (24 - 26), представлена на рис. 8. Кривая 1 соответствует , кривая 2 соответствует параметру и кривая . Как видно из рис. 8, увеличение потерь в среде распространения приводит к уменьшению уровня осцилляций ЭПР идеально проводящей сферы. Уменьшение уровня осцилляций обусловлено увеличением затухания поверхностной волны, огибающей сферу и, соответственно, уменьшением вклада, вносимого ей в ЭПР сферы.

4. Заключение

Величина ЭПР зависит от способа нормировки. Нормировка [2] приводит к тому, что ЭПР возрастает экспоненциально с ростом потерь в среде, окружающей объект, что не имеет никакого разумного физического объяснения.

При использовании предлагаемой нормировки (17), (26). ЭПР сохраняет физический смысл как для сред с потерями, так и для сред без потерь. Предлагаемая нормировка позволяет оценивать рассеивающие свойства объекта в средах с потерями. При угле двухпозиционности p, ЭПР не зависит от способа нормировки, так как в обоих случаях нормирующая амплитуда соответствует одному и тому же сечению x = 0.

Любопытно отметить, что принятая мощность , вычисленная согласно выражению (1) не зависит от способа нормировки, так как согласно [2] в выражение (1) следует подставлять дальности от антенн до "центра" объекта, в то время как в нормировке (26) или (17) участвует дальность от антенн до ближайшей (блестящей) точки на поверхности тела.

5. Выводы

1. Для корректного вычисления ЭПР в средах с потерями при нормировке следует использовать амплитуду плоской волны, соответствующей фронтальной части тела.

2. В средах с комплексной проницаемостью ЭПР зависит как от формы объекта, так и от параметров среды, окружающей объект.

3. В релеевской области рассеяния ЭПР возрастает пропорционально квадрату диэлектрической проницаемости среды, окружающей отражающий объект.

4. В резонансной области потери в среде, окружающей рассеивающий объект уменьшают амплитуду ползущей волны и, как следствие этого, уменьшаются осцилляции ЭПР.