| "ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" "JOURNAL OF RADIOELECTRONICS" N 10, 1999 |
ESTIMATION OF NOISE EQUIVALENT POWER AND DESIGN ANALYSIS OF AN ANDREEV REFLECTION HOT-ELECTRON MICROBOLOMETER FOR SUBMILLIMETER RADIOASTRONOMY
Institute of Radioengineering and Electronics RAS
received October 14, 1999
Full text in Winword format is here.
Results of theoretical estimations and measurements of characteristics of an Andreev reflection hot-electron microbolometer for submillimeter radioastronomy made by different researchers are reviewed and analysed. Peculiarities and characteristics of the microbolometers using two types of microthermometer for measurement of the electron temperature increment under influence of the radiation: the SIN-junction and the transition-edge sensor (TES) with electrothermal feedback - are compared. Advantages of the microbolometer with the second type of the microthermometer when the TES is used simultaneously as the absorber of radiation are shown. Methods of achievement of the best noise equivalent power of the microbolometer in such version as well as methods of the matching the microbolometer with the incident radiation flow using planar antennas and with the channel of output signal measurement using a SQUID-picoammeter are considered.
1. Introduction.
One of the fundamental problems of the contemporary radioastronomy [1-3] is the problem of the investigation of a celestial sphere electromagnetic radiation in the frequency region 0.3 - 3.0 THz as a result of what they are expecting an abundant information which will bring us forward to the significant broadening of our ideas about the Universe and events taking place in it. To attack this problem besides highsensitive narrowband superheterodyne receivers [4] broadband receivers of direct detection type, most sensitive among which are receivers based on hot-electron microbolometers [5-8], are necessary. The choice of two types of receivers for frequency region 0.3 - 1.5 THz [3], superheterodyne and direct detection types, is led mainly to the reason that when they are observing weak but broadband radiation sources it may occure that the sensitivity of narrowband superheterodyne receivers could be not enough and at the same time the microbolometers owing to their very wide frequency band will detect this radiation. Besides as microbolometers do not need heterodyne pumping it is much easier to construct multi-element receiving structures on their basis for an observation spatially inhomogeneous distributed radiation sources though having not too high frequency resolution. For many tasks of the submillimeter radioastronomy the noise equivalent power (NEP) of microbolometers of order 10-17 - 10-18 W· Hz-1/2 is necessary [1-3, 9] and for some tasks in future the NEP down to 10-20 - 10-21 W· Hz-1/2 will be requiered [10].
2. Andreev reflection microbolometer with a SIN-junction as the microthermometer.
Amongst mentioned above hot-electron microbolometers Andreev reflection [11] one is recognized as the most promising [7, 8] because of its comparatively simple design and lowest time constant.
The first concept of this microbolometer was proposed in [7]. In the first experiments on the realization of this concept [8] the microbolometer design was comparatively simple structure (the inset of Fig. 1) comprising a normal metal strip (Cu) with dimensions: 6-mm-long, 0.3-mm-wide, and 75-nm-thick - and lead electrodes of Al (the superconductor at temperatures < 1.2 K) deposited on the silicon substrate using the electron-beam lithography and triple-angle evaporation process. A submillimeter radiation has to be absorbed by electrons in the normal metal strip and heat them.
Fig. 1. I-V characteristics of the SIN-junction. The scheme of measurements is given at the inset: 1 - superconducting lead electrodes bringing bias current to the absorber, 2 - copper absorber, 3 - SIN-junction, 4 - superconducting electrode of SIN-junction. Solid thin curves correspond to temperatures 40 mK (right) and 300 mK (left) at zero bias current through the absorber. Dotted thick curves correspond to a base temperature of 40 mK with 20 fW (right) and 2 pW (left) power dissipated in the normal metal absorber. The power dissipated in the resistor R of the absorber is
[8].
However on account of difficulties of the
leading a radiation into the cryostat at sub-Kelvin temperatures the
measurements with the radiation in the first experiments were not made and the
heating of electrons was realized by means of the direct current biasing. Two
circumstaces lead to the effective heating of electrons: (a) the superlow
temperature (![]() 0.3 K) owing to
what the interaction between electrons and metal film through electron-phonon
collisions and therefore the energy transfer from electrons to the lattice is
extremely low, and (b) the phenomenon of Andreev reflection of electrons at the
normal metal - superconductor boundaries which takes place without the energy
transfer of electrons to the superconducting electrodes [11]. At temperatures <
1 K the electrical resistance of the normal metal strip doesn’t depend on
temperature. By this reason unlike to classic bolometers when an increment of
voltage drop caused by the absorber resistance increase owing to the temperature
increase due to the absorber heating is measured - in case of the described
microbolometer the temperature increment of electrons in the normal metal strip
is measured by means of a microthermometer which is a SIN
(superconductor-insulator-normal metal) junction. This junction was made by the
following way: before the deposition of the normal metal strip onto the silicon
substrate the 50-nm-thick and 0.2-mm-wide
strip of superconductor (Al) simultaneously with lead electrodes were deposited
under the central part of the normal metal strip (to be deposited) and after
that first one was oxidized [8]. Main results of measurements are presented at
Figures 1-3. The dependences at Fig. 2 and
Fig. 3 are obtained from the I-V
characteristics of the SIN-junction, similar to that which are presented at Fig.
1, at different temperatures and values of dissipated power of d.c. current in
copper strip. The theoretical dependece of the power dissipated by electrons in
the normal metal strip lattice through the electron-phonon interaction on
electron temperature Te and lattice temperature Tph:
0.3 K) owing to
what the interaction between electrons and metal film through electron-phonon
collisions and therefore the energy transfer from electrons to the lattice is
extremely low, and (b) the phenomenon of Andreev reflection of electrons at the
normal metal - superconductor boundaries which takes place without the energy
transfer of electrons to the superconducting electrodes [11]. At temperatures <
1 K the electrical resistance of the normal metal strip doesn’t depend on
temperature. By this reason unlike to classic bolometers when an increment of
voltage drop caused by the absorber resistance increase owing to the temperature
increase due to the absorber heating is measured - in case of the described
microbolometer the temperature increment of electrons in the normal metal strip
is measured by means of a microthermometer which is a SIN
(superconductor-insulator-normal metal) junction. This junction was made by the
following way: before the deposition of the normal metal strip onto the silicon
substrate the 50-nm-thick and 0.2-mm-wide
strip of superconductor (Al) simultaneously with lead electrodes were deposited
under the central part of the normal metal strip (to be deposited) and after
that first one was oxidized [8]. Main results of measurements are presented at
Figures 1-3. The dependences at Fig. 2 and
Fig. 3 are obtained from the I-V
characteristics of the SIN-junction, similar to that which are presented at Fig.
1, at different temperatures and values of dissipated power of d.c. current in
copper strip. The theoretical dependece of the power dissipated by electrons in
the normal metal strip lattice through the electron-phonon interaction on
electron temperature Te and lattice temperature Tph:
|
|
(1) |
where S is characterisic material parameter and v is copper strip volume, is presented.
Fig. 2. Dissipated power
for Tph= 40 mK and S= 3.7 nW· K-5m m-3:
solid curve - theory, squares - measured values [8].
At the same plot experimental points
corresponding to the dissipated d.c.power in metal strip calculated from I-V
characteristics at different temperatures are shown as well. It follows
from good agreement of the theoretical dependence and experimental points that a
predominating mechanism of electron energy flow out is the electron-phonon
interaction and other possible mechanisms do not give noticeable contribution to
this process. In the same time this means that the Andreev reflection of
electrons at the normal metal-superconductor boundaries takes place. A voltage
responsivity calculated from the dependences at Fig. 3 is 109 V/W at
temperature 100 mK, what is in good agreement with preliminary estimations of
authors of [8]. The niose voltage measured at the SIN-junction signal amplifier
input is ![]() 3 nV·
Hz-1/2 what at said above voltage responsivity corresponds to the
electrical (i.e. calculated from measurements on d.c.) noise equivalent power (NEP)
of the microbolometer equals to NEP
3 nV·
Hz-1/2 what at said above voltage responsivity corresponds to the
electrical (i.e. calculated from measurements on d.c.) noise equivalent power (NEP)
of the microbolometer equals to NEP ![]() 3·
10-18 W· Hz-1/2.
3·
10-18 W· Hz-1/2.
Fig. 3. Voltage change across the 20 kW SIN-junction as a function of power dissipated in the absorber for a bias current of Ib = 0.1 nA:
1 - T = 100 mK and 2 - T = 300 mK [8].
The results similar to described above ones are obtained in [12-14]. The difference is that an absorber was fabricated not of copper but of 3-nm-thick chrom for a better adhesion with the substrate and 35-nm-thick silver with other dimensions of 6-mm-length and 0.25-mm-width.
Fig. 4. Dependence of voltage across the SIN-junction at three values of the bias current Ib through the absorber and temperature T = 30 mK for two samples of 6-m m-length (curves 1) and 12-m m-length (curves 2) [12-14].
Besides in these works measurements of the dependence of voltage over SIN-junction on current Ib through the absorber at two its lengths: 6 and 12 mm and different SIN-junction currents I - were made (Fig. 4). Practically thedependences at two different lengths coincide. This means that the increase of the power I2b × R dissipated in the absorber due to higher resistance R has been exactly compensated by the increase of the heat conductance due to the larger volume v. This is one more confirmation that there is no substantial electron energy transport through normal metal-superconductor contacts, i.e. this is one more confirmation of the Andreev reflection at these contacts.
Initially the Andreev reflection hot-electron microbolometers with the SIN-junction microthermometer were used as X-ray detectors [15, 16].
3. Replacement of the microthermometer based on SIN-junction with a microthermometer based on superconducting transition-edge sensor.
The application of a sensor based on superconducting
transition (transition-edge sensor - TES) with strong electrothermal feedback as
a microthermometer for the microbolometer of described type using for detection
of X-rays, neutrino and other atomic particles was proposed in [17]. In such
microthermometer a superconductor or a bilayer of superconductor and normal
metal with proximity effect is in good thermal contact with an absorber of
X-rays [18], neutrino or other atomic particles. A typical electrical circuit
into which the transition-edge sensor as the microthermometer is connected is
shown at Fig. 5. The substrate with TES is cooled down to a temperature lower
than the temperature of the superconducting transition. The TES is connected in
series with the input coil of SQUID-picoammeter and the constant d.c. bias
voltage V from the shunt resistance ![]() 20
mW is applied across this series
connection.
20
mW is applied across this series
connection.
Fig. 5. Schematic of the electrical circuit used to bias the TES:
1 - TES, 2 - SQUID-amplifier input [19].
When the bias voltage is fixed at the beginning of the superconducting transition the equilibrium amount of electron energy and consequently electron temperature in the TES is automatically maintained due to an electrothermal feedback acting in the following way.
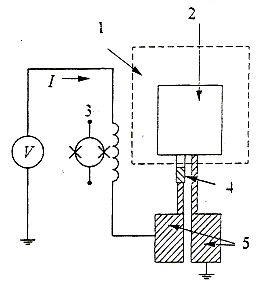
Fig. 6. Schematic of the hot-electron microbolometer for X-rays radiation measurements based on the TES with electrothermal feedback and the SQUID: 1 - Si3N4 membrane, 2 - silver absorber, 3 - SQUID, 4 - TES, 5 - aluminum contacts [18]. The Si3N4 membrane is used for the efficiency enhancement of the X-ray photon energy conversion into the electron thermal energy [15].
During the absorption of the X-ray (or
some other) radiation by the absorber (Fig. 6) electrons in the absorber are
heated and the heat spreads from these electrons to the electrons of the TES.
The TES resistance R increases with the heating of the electrons and this
leads to the decreasing of the dissipated Joule heat V2/R
(the resistance of the SQUID input coil is zero because it is made of a
superconductor). One may say that the decreasing of the power corresponding to
Joule heat dissipated in the TES is compensated by a power coming in from the
radiation. At this time the SQUID measures the decreasing of current DI
what is the output signal of microbolometer. In the described process the
replacement of the d.c. energy by the energy of absorbed radiation takes place
in the electron system and consequently this does not lead to the change of
energy flow from the electrons to the TES film lattice under the radiation
influence. By this reason the effective time constant ![]() of this process is lower of the intrinsic time constant
of this process is lower of the intrinsic time constant ![]() caused by the energy transfer from electrons to phonons in 1+a/5
times [17] where
caused by the energy transfer from electrons to phonons in 1+a/5
times [17] where
|
a=dlogR/dlogT |
(2) |
is the dimensionless measure of the sharpness of the
superconducting transition. The parameter a![]() 1.200
was obtained in the cited work, i.e.
1.200
was obtained in the cited work, i.e. ![]() /
/![]()
![]() 1:240,
what corresponds to the strong feedback.
1:240,
what corresponds to the strong feedback.
The bilayer of aluminum and silver was used as the TES in the work [18]: 30-nm-thick Ag layer was deposited first and 17-nm-thick Al layer - second. The sharp superconducting transition at temperature ~72 mK and < 1 mK width between 10 and 90% of normal resistance was obtained (Fig. 7). The I-V characteristic and the dependence of the power dissipated in TES on the bias voltage V are shown at Fig. 8. The portion of I-V curve with the negative differential resistance and the plateau at the dependence of the power dissipated in TES on the bias voltage due to the action of electrothermal feedback correspond to superconducting transition area. The described microbolometer was tested and has displaid a significantly higher sensitivity to the X-ray radiation [20] in comparison with the microbolometer based on SIN-junction microthermometer of the same authors [15, 16].
The X-ray detection microbolometer based on the TES as a part of device for measurement of the electron temperature increment of the microbolometer is described here briefly by the reason that the same principle and approximately the same scheme of a device can be used for the submillimeter radiation detection whathad been proposed in [20]. Moreover, in this work it was proposed to use the bilayer TES itself simultaneously as an absorber of radiation what increases significantly the efficiency of device. Lead electrodes bringing current to the absorber have to be made of a superconductor with significantly higher critical temperature i.e. larger energy gap in comparison with the same value of the absorber-TES structure to provide the functioning of Andreev reflection at the boundaries of the absorber and current lead electrodes [10].
Fig. 7. Characteristic of the superconducting transition of superconductor-normal metal bilayer with proximity effect: 17-nm-thick aluminum layer deposited onto 30-nm-thick argentum layer [18].
Fig. 8. I-V characteristic of the absorber combined with the TES with electrothermal feedback and corresponding dependence of power dissipated in absorber-TES on bias voltage; one may see a plateau at the power of 27 pW on the second dependence: 1 - SQUID current I, 2 - power P = I· V [18].
In the work [20] the estimations of the noise
equivalent power of such microbolometer made on the basis of measurement results
at the d.c. are given. The 70![]() 100
mm2 width-to-length Ag/Al
bilayer with total 50 nm thickness as the TES simultaneously functioning as the
absorber having temperature and electrical characteristics close to that shown
at Fig. 7 and Fig. 8 was used. Since the replacement of the part of the d.c.
power by the absorbed radiation power takes place in the microbolometer of
described type it is easy to obtain an expression for the current responsivity: Prad=
– D I·
V and the current responsivity SI=D
I / Prad=
– 1/V [17]. The beginning of the
superconducting transition in the cited work [20] takes place at V= 0.5
mV
and consequently SI= – 2·
106 A/W. The measured root-mean-square noise current of the device
was
100
mm2 width-to-length Ag/Al
bilayer with total 50 nm thickness as the TES simultaneously functioning as the
absorber having temperature and electrical characteristics close to that shown
at Fig. 7 and Fig. 8 was used. Since the replacement of the part of the d.c.
power by the absorbed radiation power takes place in the microbolometer of
described type it is easy to obtain an expression for the current responsivity: Prad=
– D I·
V and the current responsivity SI=D
I / Prad=
– 1/V [17]. The beginning of the
superconducting transition in the cited work [20] takes place at V= 0.5
mV
and consequently SI= – 2·
106 A/W. The measured root-mean-square noise current of the device
was ![]()
![]() 6
pA· Hz-1/2 what corresponds
approximately to the measurement result obtained in [21] as well. One may obtain
the NEP of microbolometer from current responsivity and root-mean-square
noise current. The result is: NEP =
6
pA· Hz-1/2 what corresponds
approximately to the measurement result obtained in [21] as well. One may obtain
the NEP of microbolometer from current responsivity and root-mean-square
noise current. The result is: NEP =![]() /|
SI |
/|
SI |![]() 3·10-18
W· Hz-1/2.
3·10-18
W· Hz-1/2.
![]()
4. Estimation of a maximum possible sensitivity of the microbolometer with TES.
The NEP of the radiation detector which utilizes a bulk (volume) detection mechanism, for example the heating of electrons or the intrinsic photoeffect (photoconductivity), and has a noise generating in the whole volume of the detector and depending on its resistance, for example the Johnson noise, is proportional to the square root of its volume v [22]
|
NEP |
(3) |
The microbolometer under consideration based on the TES combined with absorber utilizes the heating of electrons, i.e. the bulk effect, and its noise current spectral density is determined by two components [17]:
|
|
(4) |
where the first component is the Johnson noise and the second component is the phonon noise, i.e. the noise caused by thermal fluctuations during the energy exchange between electrons and phonons. Not going into details we may indicate that both components have similar dependence on the microbolometer resistance R. This means that the expression (3) is valid at two said noise components as well. In [10] the same dependence of the NEP on v is presented taking into account just the phonon noise what corresponds to the said above.
Using results of measurements of the current
sensitivity and the noise current as well as the estimation of the NEP of
the microbolometer with the TES on the basis of the said measurements in [20]
and expression (3) one may estimate the NEP of the microbolometer when
its demensions are decreased. On account of the fixed thickness of the
microbolometer (![]() 50 nm [20])
which is thicknesses sum of both layers of the bilayer determined experimentally
under condition of the obtaining the best parameters of the superconducting
transition one may modify (3) into
50 nm [20])
which is thicknesses sum of both layers of the bilayer determined experimentally
under condition of the obtaining the best parameters of the superconducting
transition one may modify (3) into
|
NEP |
(3’) |
where l is the length and w is the width of the absorber-TES. Results of the conversion of the NEP to new dimensions using (3’) are given in the next table
|
|
NEP,W/Hz-1/2 |
|
100 |
|
|
6 |
|
|
0.5 |
|
The first row (for
dimensions 100![]() 70mm2)
is the result of measurements and estimations made in [20].
70mm2)
is the result of measurements and estimations made in [20].
The second row is result of the conversion to
the dimensions ![]() of the
microbolometer with SIN-junction as microthermometer in [8] (see above) which
has the electrical noise equivalent power NEP
of the
microbolometer with SIN-junction as microthermometer in [8] (see above) which
has the electrical noise equivalent power NEP ![]() 3
×10-18
W/Hz-1/2. It is necessary to notice that said noise [8] was caused
not by the microbolometer itself but by the SIN-junction output signal amplifier
and the authors of [8] have estimated that after the reducing the noise of the
amplifier by an order it will be caused by the intrinsic noise of the
microbolometer what corresponds to an order better (lower) NEP. And even
in this case at the same dimensions like in case of the microbolometer with
SIN-junction the NEP of the microbolometer with TES will be an order
better. This is caused by the fact that whole volume of the absorber-TES is
working to generate the output signal of the microbolometer but not just a part
of the absorber overlapping with SIN-junction as in case of the microbolometer
with this junction. The experimental confirmation of the latter fact is the
independence of the output signal of the microbolometer with SIN-junction on a
power dissipated in the absorber at two its lengths (Fig. 4). In other words the
significant portion of hot electrons in the absorber in case of the
microbolometer with SIN-junction do not give contribution into output signal,
i.e. the corresponding power is lost (unused) what decreases the effectiveness
of the microbolometer. The power loss of hot electrons at 6 mm
absorber length and 0.2mm
SIN-junction width (see above) is
3
×10-18
W/Hz-1/2. It is necessary to notice that said noise [8] was caused
not by the microbolometer itself but by the SIN-junction output signal amplifier
and the authors of [8] have estimated that after the reducing the noise of the
amplifier by an order it will be caused by the intrinsic noise of the
microbolometer what corresponds to an order better (lower) NEP. And even
in this case at the same dimensions like in case of the microbolometer with
SIN-junction the NEP of the microbolometer with TES will be an order
better. This is caused by the fact that whole volume of the absorber-TES is
working to generate the output signal of the microbolometer but not just a part
of the absorber overlapping with SIN-junction as in case of the microbolometer
with this junction. The experimental confirmation of the latter fact is the
independence of the output signal of the microbolometer with SIN-junction on a
power dissipated in the absorber at two its lengths (Fig. 4). In other words the
significant portion of hot electrons in the absorber in case of the
microbolometer with SIN-junction do not give contribution into output signal,
i.e. the corresponding power is lost (unused) what decreases the effectiveness
of the microbolometer. The power loss of hot electrons at 6 mm
absorber length and 0.2mm
SIN-junction width (see above) is ![]() 97 %. At the same time a full overlapping of the SIN-junction with the absorber
appears problematic.
97 %. At the same time a full overlapping of the SIN-junction with the absorber
appears problematic.
One may obtain similar results of the
conversion of the NEP to new dimensions by means of (3’) using as a
basis the microbolometer described in [23]. It is the combined absorber-TES made
of tungsten (Tc ~95 mK of a thin W film [23]) with ![]() =
1.8
=
1.8![]() 0.9 mm2 and
thikness equal to 40 nm connected into scheme similar to Fig. 5. Its NEP
is
0.9 mm2 and
thikness equal to 40 nm connected into scheme similar to Fig. 5. Its NEP
is ![]() 3.3·
10-17 W· Hz-1/2 and the
conversion to the dimensions
3.3·
10-17 W· Hz-1/2 and the
conversion to the dimensions ![]() = 6
= 6![]() 0.3
mm2 gives NEP
0.3
mm2 gives NEP ![]() 3.5· 10-20 W·
Hz-1/2 what is close to the value in the table.
3.5· 10-20 W·
Hz-1/2 what is close to the value in the table.
The third row in the table corresponds to the
dimensions ![]() accepted for
estimations in the work [10]. In this work the thickness of microbolometer is
accepted equal to 10 nm unlike to the case of 50 nm what corresponds to
estimation results given in the table. Besides it was proposed in the said work
to increase an electron energy relaxation time in the film-absorber up to
accepted for
estimations in the work [10]. In this work the thickness of microbolometer is
accepted equal to 10 nm unlike to the case of 50 nm what corresponds to
estimation results given in the table. Besides it was proposed in the said work
to increase an electron energy relaxation time in the film-absorber up to ![]() ~ 10-3 s due to the significant decreasing of its thickness
or/and by irradiating it with high-energy ions. As the NEP depends on the
electron energy relaxation time as (
~ 10-3 s due to the significant decreasing of its thickness
or/and by irradiating it with high-energy ions. As the NEP depends on the
electron energy relaxation time as (![]() )-1/2
[10] this value has to be lower in ~70 times in comparison with the value
in the table on account of said two factors: the decrease of the film thickness
in 5 times and the increase of
)-1/2
[10] this value has to be lower in ~70 times in comparison with the value
in the table on account of said two factors: the decrease of the film thickness
in 5 times and the increase of ![]() approximately from 10-6 to 10-3 s, i.e. in 103 times.
This corresponds to NEP
approximately from 10-6 to 10-3 s, i.e. in 103 times.
This corresponds to NEP ![]()
![]() W·
Hz-1/2 and agrees with estimations in [10]. This impressive value
requires a fabrication technology on the height of contemporary technological
equipment and moves the Andreev reflection hot-electron microbolometer nearer to
the absolute receiver which NEP is determined by the quantum fluctuations
of incident radiation [22, 10].
W·
Hz-1/2 and agrees with estimations in [10]. This impressive value
requires a fabrication technology on the height of contemporary technological
equipment and moves the Andreev reflection hot-electron microbolometer nearer to
the absolute receiver which NEP is determined by the quantum fluctuations
of incident radiation [22, 10].
5. The matching of the microbolometer with the incident radiation flow and the output signal measurement channel.
It follows from the analysis made in the previous paragraphs that for the achieving the best NEP of the Andreev reflection hot-electron microbolometer one should strive for a minimum possible volume of its working part, i.e. an absorber, as well as for a method of the electron temperature increment measurement under the influence of the incident radiation giving a possibility to use the whole absorber volume what may be achived just by means of the combining the temperature increment meter with the absorber.
The second requirement can be satisfied when the superconducting transition-edge sensor (TES) with the strong electrothermal feedback as the meter of temperature increment is used. In this case as this follows from the said above the absorber of normal metal has to be replaced with the absorber of a superconductor or realized in the form of the bilayer of superconductor and normal metal where the proximity effect is observed. In both cases the material(s) of the absorber-TES have to be chosen in such way to have the superconducting transition temperature somewhat higher than the working temperature of the microbolometer and the absorber-TES has to be connected into an electrical circuit providing its operation in the strong electrothermal feedback mode.
In accordance with the first requirement the dimensions of the absorber-TES have to be chosen much less than the wavelength of the incident radiation. To match so small absorber-TES with the incident radiation flow the optical, to be precise - the quasioptical focusing of the radiation onto the absorber-TES with said dimensions is unsuitable because of the radiation diffraction fenomenon on it. By this reason the absorber-TES has to be connected into the center of a planar antenna or into a waveguide. The combination of the quasioptical focusing first, for instance by means of a lens or a horn, and then the matching by means of the planar antenna or the waveguide is possible.
Before a further consideration of the problem
of the microbolometer matching with the incident radiation flow and the output
signal measurement channel it is necessary to make more detailed estimation of
parameters of the microbolometer with the TES as the microthermometer for
instace with dimensions ![]() = 6
= 6![]() 0.3
mm2 using the
conversion method already applied above (see the table). We accept again as the
basis of the conversion the microbolometer with the dimensions
0.3
mm2 using the
conversion method already applied above (see the table). We accept again as the
basis of the conversion the microbolometer with the dimensions ![]() =
100
=
100![]() 70 mm2.
This microbolometer has the d.c. and low frequency resistance R
70 mm2.
This microbolometer has the d.c. and low frequency resistance R![]() 0.2
W (approximately like as at Fig.
7). The bilayer which serves as the TES is working as a normal metal at
frequencies of the incident radiation at
0.2
W (approximately like as at Fig.
7). The bilayer which serves as the TES is working as a normal metal at
frequencies of the incident radiation at ![]() where in given case D
is the energy gap of the bilayer structure. Besides the absorber-TES thickness
is significantly less than skin depth [7]. Owing to these circumstances the
bilayer resistance Rw
at the
incident radiation frequency w corresponds to its normal resistance:
Rw=
Rn
where in given case D
is the energy gap of the bilayer structure. Besides the absorber-TES thickness
is significantly less than skin depth [7]. Owing to these circumstances the
bilayer resistance Rw
at the
incident radiation frequency w corresponds to its normal resistance:
Rw=
Rn ![]() 1W.
Further: V
1W.
Further: V ![]() 0.5·
10-6 V, I = V/R
0.5·
10-6 V, I = V/R ![]() 2.5· 10-6 A and the noise current
2.5· 10-6 A and the noise current ![]()
![]() 6· 10-12 A·
Hz-1/2. We will carry out the conversion of these values to the
microbolometer with
6· 10-12 A·
Hz-1/2. We will carry out the conversion of these values to the
microbolometer with ![]() = 6
= 6![]() 0.3
mm2
dimensions under condition of the constant bilayer thickness as well as the
constant current density through it using the following formulae: R and
0.3
mm2
dimensions under condition of the constant bilayer thickness as well as the
constant current density through it using the following formulae: R and ![]() ,
,
![]() ,
,  (see (4)). The results of conversion are: R
(see (4)). The results of conversion are: R![]() 2.8
W, Rw
2.8
W, Rw![]() 14
W,
I
14
W,
I ![]() 1.1·
10-8 A, V = R· I
1.1·
10-8 A, V = R· I![]() 3·
10-8 V,
3·
10-8 V, ![]()
![]() 1.6·
10-12 A· Hz-1/2. Further:
SI = -1/ V
1.6·
10-12 A· Hz-1/2. Further:
SI = -1/ V ![]()
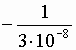 A/W,
and NEP =
A/W,
and NEP = ![]() /|
SI |
/|
SI |![]() 4.8· 10-20 W·
Hz-1/2. The latter value coincides with corresponding value in the
table what has to be. The values R, Rw ,
V and
4.8· 10-20 W·
Hz-1/2. The latter value coincides with corresponding value in the
table what has to be. The values R, Rw ,
V and ![]() are primary
parameters for the designing the microbolometer including questions of
connection the absorber-TES into electrical scheme (Fig. 5) and of the matching
it with the antenna and the absorber-TES output signal amplifier. Results of the
carried out convertion what is related to the table as well are correct when l
and w are much more than bilayer
thickness. The case when w= 0.3 mm
what is six times more than the bilayer thickness (0.05mm)
is at the margin of said relation. The 0.2 mm
width (the third row of the table) is only four times more than the bilayer
thickness. Therefore the carried out conversion should be considered as
estmation one. Precise dependences of absorber-TES characteristics on the
geometry have to be derived from an experiment.
are primary
parameters for the designing the microbolometer including questions of
connection the absorber-TES into electrical scheme (Fig. 5) and of the matching
it with the antenna and the absorber-TES output signal amplifier. Results of the
carried out convertion what is related to the table as well are correct when l
and w are much more than bilayer
thickness. The case when w= 0.3 mm
what is six times more than the bilayer thickness (0.05mm)
is at the margin of said relation. The 0.2 mm
width (the third row of the table) is only four times more than the bilayer
thickness. Therefore the carried out conversion should be considered as
estmation one. Precise dependences of absorber-TES characteristics on the
geometry have to be derived from an experiment.
(a) (b)
(c) (d)
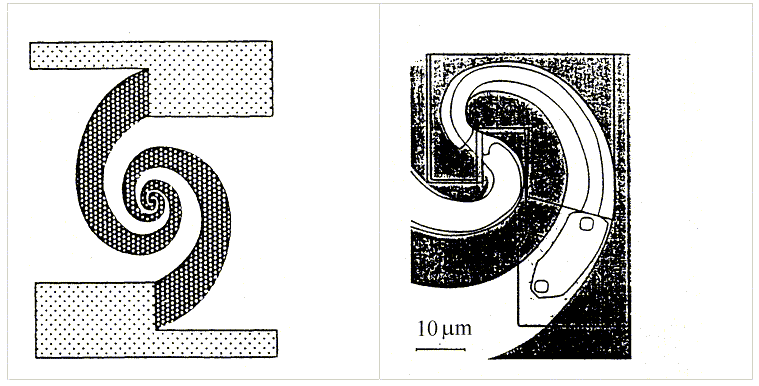
Fig. 9. Planar antennas for the matching receiving elements with the incident submillimeter radiation flow: (a) equiangular spiral antenna structure [24] for 250-800 GHz frequency band (schematic view is not in scale); (b) microphotograph of the central part of the structure at (a), two small squares are SIS-junctions which image impedance components are mutually compensated in ~400-500 GHz frequency band by means of microstrip line section, the rest portion of microstrip line is quarter-wavelength transformer matching ~10 W impedance real component of two SIS-junctions with ~114 W antenna output impedance; (c) microphotograph of planar log-periodic antenna [12-14] designed for the matching the microbolometer with SIN-junction of several tens W resistance with ~114 W antenna output impedance; (d) 110 GHz double-slot antenna for the matching GaAs mixer: 1, 3 - slots, 2 - GaAs mixer, 4 - microstrip line for intermediate frequency signal lead out with connected into it GaAs mixer and cut-off filters at signal and heterodyne frequencies, 5 - quartz substrate for the microstrip line, 6 - gold film deposited onto dielectric [25].
The experience of the submillimeter waveband receivers
development on the basis of SIS-mixers (see for example [24]) shows that planar
antennas are better than waveguides for the purposes of the matching receiving
elements of small dimensions with the incident radiation flow because they may
be deposited onto the substrate together with a receiving element, in our case
with the microbolometer. Planar antennas can be spiral, log-periodic,
double-slot (Fig. 9) [24, 12-14,
25] or of other types. They as it was said are
fabricated by microfilm technology methods and the receiving elements are
integrated into them. Of course it is necessary to take care of antenna to be
made of material with minimum absorbtion of radiation. It is best of all to
fabricate the antenna of a superconductor with the energy gap D
more than ![]() of the incident
radiation so as the antenna material to be superconducting at incident radiation
frequencies. May be it will be necessary to coat most of the antenna surface
with well conducting normal metal. In case when the antenna made of
superconductor it may function as two electrodes as well bringing the bias
current to the absorber-TES what will provide the Andreev reflection at the
boundaries between the absorber-TES and the antenna. The efficiency of said
above antennas is not less than 50% what means that not less than 50% of the incident
radiation power is absorbed by the matched load in the antenna center. The
matching problem of a microbolometer impedance of order of 10-15 W
or less with the output impedance ~120 W of the antenna deposited onto dielectric substrate, for instance quartz or
silicon, may be solved by means of the connection between the absorber-TES and
the antenna output the microstrip transformer of l/4
length, where l is the wavelength of
the incident radiation, fabricated using thin-film technology methods like it
was made for instance in [24] for the case of SIS-mixer (Fig. 9,a and
Fig. 9,b).
of the incident
radiation so as the antenna material to be superconducting at incident radiation
frequencies. May be it will be necessary to coat most of the antenna surface
with well conducting normal metal. In case when the antenna made of
superconductor it may function as two electrodes as well bringing the bias
current to the absorber-TES what will provide the Andreev reflection at the
boundaries between the absorber-TES and the antenna. The efficiency of said
above antennas is not less than 50% what means that not less than 50% of the incident
radiation power is absorbed by the matched load in the antenna center. The
matching problem of a microbolometer impedance of order of 10-15 W
or less with the output impedance ~120 W of the antenna deposited onto dielectric substrate, for instance quartz or
silicon, may be solved by means of the connection between the absorber-TES and
the antenna output the microstrip transformer of l/4
length, where l is the wavelength of
the incident radiation, fabricated using thin-film technology methods like it
was made for instance in [24] for the case of SIS-mixer (Fig. 9,a and
Fig. 9,b).
The SQUID-picoammeter with the subsequent
amplifying stages is the best solution for the measurement of the output signal
of the Andreev reflection hot-electron microbolometer because the noise current
of the best SQUID-picoammeters is ![]()
![]() 0.5 pA·
Hz-1/2 [21] what is approximately three times less in comparison with
the estimated above intrinsic noise current of the microbolometer at the ~5-10 W
resistance. The scheme of connection of the microbolometer with the combined
absorber-TES into the electrical circuit is the same as at Fig. 5 just with the
replacement of the inscription “TES” for “absorber-TES”.
0.5 pA·
Hz-1/2 [21] what is approximately three times less in comparison with
the estimated above intrinsic noise current of the microbolometer at the ~5-10 W
resistance. The scheme of connection of the microbolometer with the combined
absorber-TES into the electrical circuit is the same as at Fig. 5 just with the
replacement of the inscription “TES” for “absorber-TES”.
6. Conclusion.
The important results of the first works on investigation of the normal metal hot-electron microbolometer with SIN-junction for the measurement of the electron temperature increment due to the radiation absorption are the experimental confirmation of the Andreev reflection of electrons at the boundaries of the normal metal absorber and the superconducting lead electrodes when hot electron energy does not flow out from the absorber to the electrodes as well as the estimation of the noise equivalent power of such microbolometer. As the consequence of review and comparison of the different research results on the Andreev reflection hot-electron microbolometer made in the present work the advantage of the superconducting transition-edge sensor (TES) with electrothermal feedback used as the microthermometer for such microbolometer in comparison with SIN-junction sensor for the same purpose is shown. The reason of this advantage is that whole volume of the absorber participates in the generation of the microbolometer output signal in case of the combined absorber-TES when only part of the absorber does this in case of SIN-junction sensor. On account of this fact the microbolometer with the TES combined with the absorber has at least one order better (lower) noise equivalent power (NEP) in comparison with the microbolometer with SIN-junction having the same absorber dimentions. In the first case the absorber-TES has to be made of a superconductor or as an bilayer of superconductor and normal metal with the proximity effect under condition that the superconducting transition temperature has to be somewhat higher than the microbolometer temperature as well as the bias d.c. current and radiation lead electrodes to the absorber-TES have to be fabricated of a superconductor with the energy gap much higher in comparison with this value of the absorber-TES. The main way to achive the best NEP of said microbolometer is the reducing of absorber-TES dimensions limited by technology possibilities and the application of the planar antenna for the matching with the incident radiation as well as the extralow-noise front-end SQUID-picoammeter with SQUID input coil connected in series with the absorber-TES for the microbolometer output signal amplification. At present time experiments for the realization of proposed solutions are preparing.
The author thanks Academician A.F. Andreev and Academician N.S. Kardashev for the stimulation of this work and J.M. Martinis, K.D. Irwin, P.L. Richards, B.S. Karasik and M.A. Tarasov for useful discussions and suggestions. This work is supported by the International Science and Technology Center (Project N 1239).
References.
1. Gromov V.D., Kardashev N.S., Kurt V.D.
et al. // The![]() Project “Submillimetron”,
Scientific Session of the Astro Space Center of the P.N. Lebedev Physics
Institute of RAS, Pushchino, January 1998 (in Russian).
Project “Submillimetron”,
Scientific Session of the Astro Space Center of the P.N. Lebedev Physics
Institute of RAS, Pushchino, January 1998 (in Russian).
2. Kuzmin L.S., Kardashev N.S., Kurt V.G. et al. // Proc. of ESTEC
Workshop. Noordwijk. November 1998. P. 127.
3. Vystavkin A.N., Chuvaev D.V., Claeson T. et al. // Proc. of 10-th Symposium on Space Terahertz Technology. Charlottesville. USA. March 1999. P. 372.
4. Whyborn N.D. // Proc. of ESA Symposium devoted to the Far InfraRed and Submillimeter Telescope (FIRST) mission. Grenoble. France. Institut de Radio Astronomie Millimetrique. April 1997. P. 19.
5. Griffin M.J. // ibid., P. 31.
6. Bock J.J., LeDuc H.G., Lange A.E., Zmuidzinas J. // ibid., P. 349.
7. Nahum M., Richards P.L., Mears C.A. // IEEE Transactions on Applied Superconductivity. 1993. V. 3. N. 1. P. 2124.
8. Nahum M., Martinis J.M. // Appl. Phys. Lett. 1993. V. 63. N. 23. P. 3075.
9. Eurepean Space Agency Tender AO3370 “Hot-electron Microbolometer Technology for IR and Sub-mmw Application”. Open Date: Oct. 2. 1997.
10. Karasik B.S., McGrath W.R., LeDuc H.G., Gershenson M.E. // Extended Abstracts of the 7-th International Superconductive Electronics Conference ISEC’99. Berkeley. USA. June 1999. P. 524.
11. Andreev A.F. // Sov. Phys. JETP. 1964. V. 19. N. 11. P. 1228.
12. Vystavkin A.N., Chouvaev D.V., Kuzmin L. et al. // Proc. of the 4-th International Conference on Millimeter and Submillimeter Waves and Applications. San Diego. USA. July 1998. P. 441.
13. Chuvaev D.V, Kuzmin L.S., Tarasov M.A. et al. // Proc. of the 9-th International Symposium on Space Terahertz Technology. Pasadena. USA. March 1998. P. 331.
14. Vystavkin A.N., Chouvaev D.V., Kuzmin L. et al. // J. of Exp. and Theor. Physics. 1999. V. 88. N. 3. P. 598.
15. Nahum M., Martinis J.M. // Appl. Phys. Lett. 1995. V. 66. N 23, P. 3203.
16. Martinis J.M. // NIM. 1996. V. A370 . P. 171.
17. Irwin K.D. // Appl. Phys. Lett. 1995. V. 66. N. 15. P.1998.
18. Irwin K.D., Hilton G.C., Martinis J.M., Cabrera B. // NIM. 1996. V. A370. P.177.
19. Nam S.W., Cabrera B., Chugg B. et al. // NIM. 1996. V. A370. P.187.
20. Irwin K.D., Hilton G.C., Wolman D.A., Martinis J.M. // Appl. Phys. Lett. 1996. V. 69. N. 13. P. 1945.
21. Lee A.T., Lee S.-F., Gildemeister J.M., Richards P.L. // Proc. of 7-th Symp. on Low Temp. Detectors. 27 July - 2 August 1997. Munich. P. 123.
22. Vystavkin A.N., Migulin V.V. // Radiotekhnika i Elektronika. 1967. V. 12. N. 11. P. 1989 (in Russian).
23. Lee A.T., Richards P.L., Nam S.W. et al. // Appl. Phys. Lett. 1966. V. 69. N. 12. P. 1801.
24. Belitsky Yu.V., Yacobson S.V., Filippenko L.V. at al. // Journal of Communications Technology and Electronics. 1996. V. 41. N. 1. P. 113.
25. Rebeiz G.M. // Proc. of the IEEE. 1992. V. 80. N. 11. P. 1748.