

Next: Approximation of the Test-Statistic
Up: Approximation of distribution function
Previous: Problem Formulation
In order to evaluate 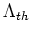 for a given
for a given 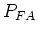 it is necessary to know the PDF (or the CDF) of the test-statistic
it is necessary to know the PDF (or the CDF) of the test-statistic 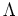 .
While the PDF of the random variable
.
While the PDF of the random variable 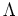 is not known in analytical
closed form, the exact analytical expression of the statistical moments
of any order for the test-statistic monotonic function
is not known in analytical
closed form, the exact analytical expression of the statistical moments
of any order for the test-statistic monotonic function 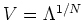 can be found by using the well-known complex
Wishart distribution
for the matrix
can be found by using the well-known complex
Wishart distribution
for the matrix 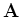 given in [3]
given in [3]
|
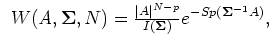
|
|
|
(7) |
where
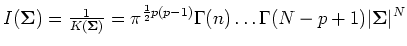
If the null hypothesis 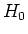 is true, the matrix
is true, the matrix 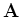 is
is
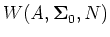 distributed.
distributed.
The 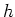 -th order moment of the random variable
-th order moment of the random variable
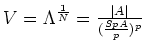
can be straightforward determined from multidimensional
integral
|
![$\displaystyle \begin{array}{l}
M[V^h]=\int...\int\vert A\vert^h\frac{1}{\biggl(...
... _0,N)\times \ \times
\vert A\vert^{N-p}exp{[-Sp(\S _0^{-1}A)]dA}
\end{array}$](img44.png)
|
|
|
(8) |
The integration procedure is carry out here over area
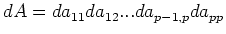 , where A are all
non-negative defined Hermitian
, where A are all
non-negative defined Hermitian ![$[p \times p]$](img46.png) matrices. The
integral (8) can be transformed into
matrices. The
integral (8) can be transformed into
|
![$\displaystyle \begin{array}{l}
M[V^h]=\frac {p^{hp}K(\S _0,N)} {K(\S _0,N+h)}\i...
...xp[-Sp(\S _0^{-1}A)]\}
\frac{1}{(\sum\limits_{i=1}^pa_{ii})^{ph}}dA
\end{array}$](img47.png)
|
|
|
(9) |
The element of integration (9) in figured
brackets is also Wishart distribution (7)
with 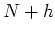 degrees of freedom
degrees of freedom
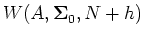 . After
integration of (9) over all nondiagonal
. After
integration of (9) over all nondiagonal
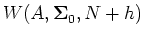 distribution elements
distribution elements 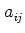
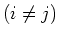 , the partial joint distribution of the diagonal elements
, the partial joint distribution of the diagonal elements
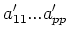 of the matrix
of the matrix 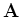 is obtained. For
hypothesis
is obtained. For
hypothesis 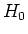 this distribution is transformed into
product of one-dimensional distributions
this distribution is transformed into
product of one-dimensional distributions
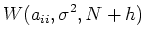 . The one-dimensional complex Wishart
distribution
. The one-dimensional complex Wishart
distribution
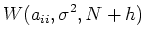 is the distribution
of the
is the distribution
of the 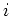 -th diagonal element of the matrix
-th diagonal element of the matrix 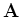 . Note,
that
. Note,
that
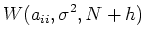 is
is 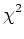 distribution
with
distribution
with 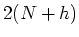 degrees of freedom:
degrees of freedom:
|
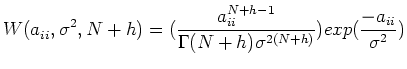
|
|
|
(10) |
Thus, the expression for the 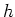 -th order moment of the
test-statistic
-th order moment of the
test-statistic 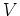 can be reduced to the integral
can be reduced to the integral
![$M[V^h]=\underbrace{p^{hp}\frac{K(\S _0,N)}{K(\S _0,N+h)}}_{g}\int...\int
\frac{...
...}{{\bf\sigma}^2}}}{{\bf\sigma}^{2(N+h)}\Gamma(N+h)}
da_{11}da_{22}\dots da_{pp}$](img57.png)
and can be represented as
![$M[V^h]=g<\frac{1} {(\sum\limits_{i=1}^pa_{ii}')^{ph}}> $](img58.png) ,
,
where 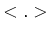 denotes expectation value.
denotes expectation value.
Diagonal elements 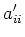 of the matrix
of the matrix 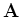 are
independent and identically
are
independent and identically 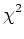 distributed random
values with
distributed random
values with 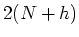 degrees of freedom and variances
degrees of freedom and variances
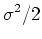 . Therefore, the random variable
. Therefore, the random variable
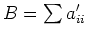 is
also
is
also 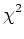 distributed with
distributed with 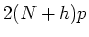 degrees of freedom.
Thereby,
degrees of freedom.
Thereby, 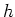 -th order moment of the random variable
-th order moment of the random variable 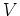 is
proportional to the
is
proportional to the 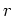 -th order moment
-th order moment 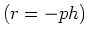 of the
random variable
of the
random variable 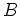 which can be expressed through known
one-dimensional integral
which can be expressed through known
one-dimensional integral
|
![$\displaystyle \begin{array}{l}
M[B^r]=\int\limits_0^{\infty}B^r\frac{B^{(N+h)p-...
...c{{\bf\sigma}^{2Np}\Gamma(Np)}{{\bf\sigma}^{2(N+h)p}\Gamma((N+h)p)}
\end{array}$](img67.png)
|
|
|
(11) |
For practical calculations of the high order moments of the
test-statistic 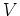 it is conveniently to transform the last
expression into product using properties of gamma-function:
it is conveniently to transform the last
expression into product using properties of gamma-function:
![$M[V^h]=g\frac{{\bf\sigma}^{2pN}\Gamma(pN)}{{\bf\sigma}^{2p(N+h)}\Gamma(p(N+h))}...
...\times\ \times\frac
{\Gamma(N+h)...\Gamma(N+h-p+1)}{\Gamma(N)...\Gamma(N-p+1)}$](img68.png)
So, the exact analytical expression for the 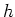 -th order moment of the test-statistic
-th order moment of the test-statistic 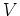 is
is
|
![$\displaystyle M[V^h]=
p^{hp}\frac{\prod\limits_{i=1}^{p}\prod\limits_{j=1}^{h}(j+N-i)}{\prod\limits_{i=1}^{ph}(i+pN-1)}$](img69.png)
|
|
|
(12) |
It is easy to see that the distribution of the random
variable 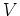 is concentrated in interval [0,1]. So, there
are moments of any order (12) for
is concentrated in interval [0,1]. So, there
are moments of any order (12) for 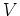 , and
they completely determine its distribution
function [5]. It is worth to notice that the
characteristic function of the random variable
, and
they completely determine its distribution
function [5]. It is worth to notice that the
characteristic function of the random variable 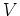 is
expressed through moments as a converging Taylor series.
is
expressed through moments as a converging Taylor series.



Next: Approximation of the Test-Statistic
Up: Approximation of distribution function
Previous: Problem Formulation
![]()
![]() is true, the matrix
is true, the matrix ![]() is
is
![]() distributed.
distributed.
![]() -th order moment of the random variable
-th order moment of the random variable
![]()
![$M[V^h]=\underbrace{p^{hp}\frac{K(\S _0,N)}{K(\S _0,N+h)}}_{g}\int...\int
\frac{...
...}{{\bf\sigma}^2}}}{{\bf\sigma}^{2(N+h)}\Gamma(N+h)}
da_{11}da_{22}\dots da_{pp}$](img57.png)
![$M[V^h]=g<\frac{1} {(\sum\limits_{i=1}^pa_{ii}')^{ph}}> $](img58.png) ,
,
![]() denotes expectation value.
denotes expectation value.
![]() of the matrix
of the matrix ![]() are
independent and identically
are
independent and identically ![]() distributed random
values with
distributed random
values with ![]() degrees of freedom and variances
degrees of freedom and variances
![]() . Therefore, the random variable
. Therefore, the random variable
![]() is
also
is
also ![]() distributed with
distributed with ![]() degrees of freedom.
Thereby,
degrees of freedom.
Thereby, ![]() -th order moment of the random variable
-th order moment of the random variable ![]() is
proportional to the
is
proportional to the ![]() -th order moment
-th order moment ![]() of the
random variable
of the
random variable ![]() which can be expressed through known
one-dimensional integral
which can be expressed through known
one-dimensional integral
![$M[V^h]=g\frac{{\bf\sigma}^{2pN}\Gamma(pN)}{{\bf\sigma}^{2p(N+h)}\Gamma(p(N+h))}...
...\times\ \times\frac
{\Gamma(N+h)...\Gamma(N+h-p+1)}{\Gamma(N)...\Gamma(N-p+1)}$](img68.png)
![]() -th order moment of the test-statistic
-th order moment of the test-statistic ![]() is
is